جداء ثلاثي
في الرياضيات، جداء ثلاثي (بالإنجليزية: Triple product) هو حاصل ضرب ثلاثة متجهات. وتكون نتيجته إما «جداء ثلاثيا غير متجه» أو «جداء ثلاثيا متجها» وهذا الأخير يحدث نادرا في الفيزياء.
جداء ثلاثي غير متجه
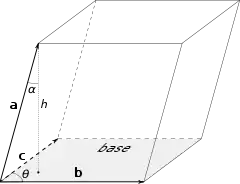
يعرّف الجداء الثلاثي غير المتجه بأنه حاصل ضرب جداء قياسي لأحد المتجهات في جداء اتجاهي.
خواصه
- لا يتأثر الجداء الثلاثي غير المتجة بالإزاحة الدورانية ويتكون من ثلاثة متجهات (a, b, c):
- استبدال المتجهين في الجداء الاتجاهي يعكس إشارة ناتج الجداء الثلاثي:
ترميزات مستخدمة أخرى
تستخدم بعض الرميزات الأخرى للتعبير عن الضرب الثلاثي غير المتجه مثل: .
وكذلك: و .
شرح الخواص
عملية الضرب الثلاثي غير المتجه ليست عملية تبديلية. ولكن قيمته لا تتغير إذا بادلنا المعاملات تبديلا دورانيا:
- .
- ويمكن حساب الجداء الثلاثي بواسطة المحددات، فمثلا ينطبق علي المعادلة:
ينطبق عليها أن يكون:
ويمكن إثبات ذلك بإجراء الحساب:
- حيث أن الضرب القياسي يكون عملية تبديلية، فنحصل على:
- .
أي باختيار أقواسا مناسبة يمكن تبديل العلامات الحسابية.
- وبعكس التبادل الدوراني ينتج عند إجراء تبادل دوراني مضاد تغيير للإشارة:
- كما أنه نظرا إلى أن يكون:
- والضرب في كمية غير متجهة تنتج:
وهي عملية تسمى عملية تجميعية.
جداء ثلاثي متجه
يعرف الجداء الثلاثي المتجه بإنه ضرب اتجاهي لمتجه مضروبا في ضرب اتجاهي آخر. وتنطبق عليه القاعدة التالية:
- .
تعرف المعادلة الأولى بأنها «معادلة لاجرانج» أو «الضرب الثلاثي الممتد» [1][2]
ويمكن تذكر الجزء الأيمن من المعادلة بالترميز "BAC - CAB" مع تذكر أي متجهات تكون فيها عملية الضرب قياسية (علامة الضرب «النقطية»).
ولإثبات ذلك نبدأ بالمعادلات التي تسهل حسابات المتجهات في الفيزياء. ومن ضمنها معادلات التدرج - مثل تدرج مجال مغناطيسي أو تدرج درجات الحرارة وهي تدرجات تنتسب إلى تغير المكان - وتسهل حسابات المتجهات: [3]
حيث هي مؤثر لابلاس.
انظر أيضا
مراجع
- جوزيف لوي لاغرانج did not develop the cross product as an algebraic product on vectors, but did use an equivalent form of it in components: see Lagrange, J-L (1773)، "Solutions analytiques de quelques problèmes sur les pyramides triangulaires"، Oeuvres، ج. vol 3.
{{استشهاد بكتاب}}:|المجلد=has extra text (مساعدة) He may have written a formula similar to the triple product expansion in component form. See also Lagrange's identity and كيوشي إيتو (1987)، Encyclopedic Dictionary of Mathematics، MIT Press، ص. 1679، ISBN 0-262-59020-4. - كيوشي إيتو (1993)، "§C: Vector product"، Encyclopedic dictionary of mathematics (ط. 2nd)، MIT Press، ص. 1679، ISBN 0-262-59020-4، مؤرشف من الأصل في 31 أكتوبر 2014.
- Pengzhi Lin (2008)، Numerical Modelling of Water Waves: An Introduction to Engineers and Scientists، Routledge، ص. 13، ISBN 0-415-41578-0، مؤرشف من الأصل في 2 ديسمبر 2016.
وصلات خارجية
- بوابة رياضيات
- بوابة جبر