دلتاهيدرون
الدلتاهدرون (بالإنجليزية: Deltahedron) (الجمع دلتا السطوح) (باليونانية: Δ) في الهندسة هو متعدد الوجوه الذي تكون وجوهه كلها مثلثات متساوية الأضلاع. الاسم مأخوذ من الحالة اليونانية العليا دلتا (Δ) ، والتي لها شكل مثلث متساوي الأضلاع. هناك عدد لانهائي من مناطق الدلتاهيدرا ، وكلها لها عدد زوجي من الوجوه بسبب المصافحة الليفية. من بين هؤلاء ثمانية فقط محدبة ، لها 4 و 6 و 8 و 10 و 12 و 14 و 16 و 20 وجهًا. [1] عدد الوجوه والحواف والرؤوس مذكور أدناه لكل من الثماني وجوه المحدبة.
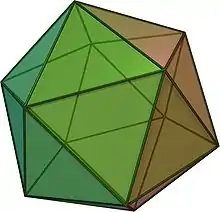

ثمانية محدب السطوح
لا يوجد سوى ثمانية أشكال دلتا محدبة بدقة: ثلاثة منها متعددة الوجوه العادية، وخمسة هي مواد صلبة من جونسون.
| دلتاهدرا العادية | ||||||
|---|---|---|---|---|---|---|
| صورة | اسم | وجوه | حواف | الرؤوس | تكوينات فيرتكس | مجموعة التماثل |
| رباعي الوجوه | 4 | 6 | 4 | 4 × 33 | Td, [3,3] | |
| المجسم الثماني | 8 | 12 | 6 | 6 × 34 | Oh, [4,3] | |
| عشري الوجوه | 20 | 30 | 12 | 12 × 35 | Ih, [5,3] | |
| جونسون دلتا | ||||||
| صورة | اسم | وجوه | حواف | الرؤوس | تكوينات فيرتكس | مجموعة التماثل |
| مثلث ثنائي الهرم | 6 | 9 | 5 | 2 × 33
3 × 34 |
D3h, [3،2] | |
| هرم مزدوج | 10 | 15 | 7 | 5 × 34
2 × 35 |
D5h, [5،2] | |
| Snub disphenoid [الإنجليزية] | 12 | 18 | 8 | 4 × 34
4 × 35 |
D2d, [2،2] | |
| المنشور الثلاثي المعزز | 14 | 21 | 9 | 3 × 34
6 × 35 |
D3h, [3,2] | |
| بيراميد دائري طويل الشكل | 16 | 24 | 10 | 2 × 34
8 × 35 |
D4d, [4,2] | |
في دلتا السطوح ذات 6 أوجه، بعض الرؤوس لها درجة 3 وبعض الدرجة 4. في دلتا السطوح ذات 10 و 12 و 14 و 16 وجهًا ، تحتوي بعض الرؤوس على درجة 4 وبعض الدرجة 5. تنتمي هذه الدلتاهدرا الخمسة غير المنتظمة إلى فئة أجسام جونسون الصلبة : الأشكال المتعددة السطوح المحدبة ذات المضلعات المنتظمة للوجوه.
تحتفظ منطقة Deltahedra بشكلها حتى لو كانت الحواف حرة في الدوران حول رؤوسها بحيث تكون الزوايا بين الحواف سائلة. لا تمتلك كل متعددات الوجوه هذه الخاصية: على سبيل المثال، إذا قمت بإرخاء بعض زوايا المكعب، فيمكن أن يتشوه المكعب إلى منشور مربع غير يميني.
لا يوجد دلتا وجه محدب 18 وجهًا. [2] ومع ذلك، فإن الحافة العشرية الوجوه المتعاقد عليها تعطي مثالًا على ثماني وجوه يمكن أن تكون محدبة مع 18 وجهًا مثلثًا غير منتظم، أو مصنوعة من مثلثات متساوية الأضلاع تتضمن مجموعتين متحدتين من ثلاثة مثلثات.
حالات غير محدبة بدقة
هناك العديد من الحالات التي تحتوي على مثلثات متحد المستوى ، مما يسمح بوجود أقسام من الأسطح المثلثية اللانهائية. إذا اعتبرت مجموعات المثلثات متحد المستوى وجهًا واحدًا ، فيمكن حساب مجموعة أصغر من الوجوه والحواف والرؤوس. يمكن دمج الوجوه المثلثة متحد المستوى في وجوه معينية أو شبه منحرفة أو سداسية أو غيرها من أوجه المضلع متساوية الأضلاع. يجب أن يكون كل وجه محدبًا متعدد الألماس مثل:
![]() و
و![]() و
و![]() و
و![]() و
و![]() و
و![]() و
و![]() و
و![]() [3]
[3]
أشكال غير محدبة
هناك عدد لا حصر له من أشكال غير محدبة. بعض الأمثلة على تقاطع الوجه الدلتا:
- عشري الوجوه الكبير - مادة صلبة كبلر-بوينسوت، مع 20 مثلثات متقاطعة
يمكن إنشاء دلتا السطوح الأخرى غير المتقاربة عن طريق إضافة أهرامات متساوية الأضلاع إلى وجوه جميع متعددات الوجوه الخمسة العادية:
| ترياكيس رباعي السطوح | تتراكيس سداسي الوجوه | ترياكيس ثماني السطوح ( ستيلا أوكتانجولا ) |
البنتاكيس ثنائي الوجوه | ترياكيس عشري الوجوه |
|---|---|---|---|---|
| 12 مثلثا | 24 مثلثا | 60 مثلثات | ||
تشمل الزيادات الأخرى في رباعي الوجوه ما يلي:
| 8 مثلثات | 10 مثلثات | 12 مثلثا |
|---|
وأيضًا بإضافة الأهرامات المقلوبة إلى الوجوه:
- اثني عشر وجهًا محفورًا
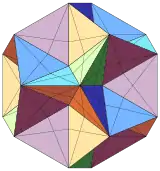 اثني عشر وجهًا محفورًا |
 مثلث السطوح الحلقي |
| 60 مثلثات |
|---|
المراجع
- Freudenthal, H؛ van der Waerden, B. L. (1947)، "Over een bewering van Euclides ("On an Assertion of Euclid")"، Simon Stevin (باللغة الهولندية)، ج. 25، ص. 115–128 (They showed that there are just 8 convex deltahedra. )
- Trigg, Charles W. (1978)، "An Infinite Class of Deltahedra"، Mathematics Magazine، ج. 51، ص. 55–57، doi:10.1080/0025570X.1978.11976675، JSTOR 2689647.
- The Convex Deltahedra And the Allowance of Coplanar Faces نسخة محفوظة 2020-10-26 على موقع واي باك مشين.
قراءة متعمقة
- Rausenberger, O. (1915)، "Konvexe pseudoreguläre Polyeder"، Zeitschrift für mathematischen und naturwissenschaftlichen Unterricht، ج. 46، ص. 135–142.
- Cundy, H. Martyn (ديسمبر 1952)، "Deltahedra"، Mathematical Gazette، ج. 36، ص. 263–266، doi:10.2307/3608204، JSTOR 3608204.
- Cundy, H. Martyn؛ Rollett, A. (1989)، "3.11. Deltahedra"، Mathematical Models (ط. 3rd)، Stradbroke, England: Tarquin Pub.، ص. 142–144.
- Gardner, Martin (1992)، Fractal Music, Hypercards, and More: Mathematical Recreations from Scientific American، New York: W. H. Freeman، ص. 40, 53, and 58-60.
- Pugh, Anthony (1976)، Polyhedra: A visual approach، California: University of California Press Berkeley، ISBN 0-520-03056-7 pp. 35–36
روابط خارجية
- بوابة هندسة رياضية
- بوابة هندسة
- بوابة رياضيات