دالة رتيبة

في الرياضيات، الدالة الرتيبة (بالإنجليزية: Monotonic function)‏ هي دالة تحافظ على ترتيب ما.[1][2][3] نشأ مصطلح الدالة الرتيبة من حساب التفاضل والتكامل وعمّم لاحقًا لما يطلق عليه اسم نظرية الترتيب.

رسم 1: دالة رتيبة تصاعدية (في بعض أجزائها، فإنّ الدالة مجرد دالة رتيبة غير تنازلية، وفي باقي الأجزاء فالدالة تصاعدية تمامًا).

رسم 2: دالة رتيبة تنازلية.

رسم 3: دالة غير رتيبة.

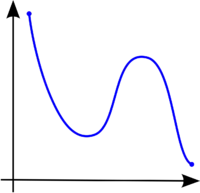
الدوال الرتيبة في التحليل الرياضي وحساب التفاضل والتكامل

في سياق التحليل الرياضي وحساب التفاضل والتكامل، تدعى الدالة الحقيقيّة f المعرفة على مجموعة جزئية من الأعداد الحقيقية دالة رتيبة تصاعدية (أو متزايدة)، إذا كان لكل x ≤ y يتحقّق أيضًا $f(x)\leq f(y)$ ، أي أنّها تحافظ على الترتيب (أنظر رسم 1). وبحسب نفس المنطق، فإنّ f رتيبة تنازلية (أو متناقصة) إذا كان لكل x ≤ y يتحقّق أيضًا $f(x)\geq f(y)$ ، أي أنّ الدالة تعكس الترتيب (أنظر رسم 2).

إذا ما استبدلت إشارات «الأكبر أو يساوي» ≤ بإشارات «أكبر من» < نحصل على شرط أقوى. في هذه الحالة يطلق على الدوال اسم تصاعدية تمامًا أو تنازلية تمامًا بالتناظر. ومن خواص هذه الدوال أنّها دوال متباينة (أي بالإمكان تعريف دالة عكسية لها)، أذ أنّه إذا كان لـx ولـy قيمتان مختلفتان، فإمّا أن يكون x < y أو x > y، وحسب نوع الدالة الرتيبة (تصاعدية أم تنازلية تمامًا) يكون $f(x)<f\left(y\right)$ أو $f(x)>f\left(y\right)$ ، وعلى كل حال فإنّ $f(x)\neq f(y)$ وهو ما يجعلها دالة واحد لواحد.

بعض الخواص والنتائج الأساسية

الخواص التالية صحيحة لأي دالة رتيبة $f:\mathbb {R} \to \mathbb {R}$ :

للدالة f نهاية من اليمين ومن اليسار في كل نقطة من نطاق الدالة؛
للدالة f نهاية في اللانهاية (في $\infty$ و $-\infty$ )، وقد تكون تلك إمّا عددًا حقيقيًا أو $\infty$ أو $-\infty$ ؛
أيّة نقاط نقاط عدم استمرار للدالة f تكون حتمًا من نوع قفزة؛

انظر أيضًا

مراجع

The Integrals of Lebesgue, Denjoy, Perron, and Henstock، AMS، 1994، ISBN 978-0-82183805-1، 55-56 {{استشهاد بكتاب}}: يحتوي الاستشهاد على وسيط غير معروف وفارغ: |month= (مساعدة)، الوسيط |first= يفتقد |last= (مساعدة)
Real Analysis، 1997، ISBN 978-0-13458886-5، 269 {{استشهاد بكتاب}}: يحتوي الاستشهاد على وسيط غير معروف وفارغ: |month= (مساعدة)، الوسيط |first= يفتقد |last= (مساعدة)
قالب:Note autre projet

بوابة رياضيات
بوابة تحليل رياضي

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] The Integrals of Lebesgue, Denjoy, Perron, and Henstock، AMS، 1994، ISBN 978-0-82183805-1، 55-56 {{استشهاد بكتاب}}: يحتوي الاستشهاد على وسيط غير معروف وفارغ: |month= (مساعدة)، الوسيط |first= يفتقد |last= (مساعدة)

[2] Real Analysis، 1997، ISBN 978-0-13458886-5، 269 {{استشهاد بكتاب}}: يحتوي الاستشهاد على وسيط غير معروف وفارغ: |month= (مساعدة)، الوسيط |first= يفتقد |last= (مساعدة)

[3] قالب:Note autre projet