قائمة مساقط الخرائط

هذا ملخص لمساقط الخرائط. نظرًا لعدد مساقط الخرائط المحتملة غير منتهية،[1] لا يمكن أن تكون هناك قائمة شاملة.

جدول المساقط
الإسقاط الصورة النوع الخصائص المخترع السنة الملاحظات
إسقاط متساوي المستطيلات

= أسطواني متساوي المسافات = مستطيلية

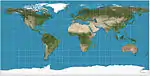 أسطواني متساوي المسافات مارينوس الصوري 120ق. 120 أبسط هندسة؛ المسافات على طول خطوط الطول محفوظة.
إسقاط كاسيني

= كاسيني–سولدنر

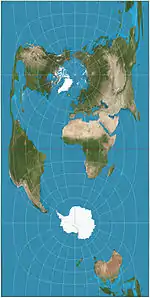 أسطواني متساوي المسافات سيزار فرانسوا كاسيني 1745 إسقاط متساوي البعد عرضي؛ المسافات على طول خط الزوال المركزي محفوظة.

المسافات العمودية على خط الطول المركزي محفوظة.

إسقاط مركاتور 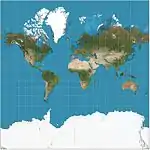أسطواني محافظ (Conformal) جيراردوس مركاتور 1569 خطوط الاتجاه الثابتة مستقيمة، تساعد على الملاحة. تضخم المساحات مع خطوط العرض تصبح شديدة لدرجة أن الخريطة لا يمكنها إظهار القطبين.
إسقاط مركاتور للويب 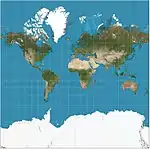أسطواني توفيقي

(Compromise)

 جوجل 2005 نوع من المركاتور يتجاهل إهليلجية اللأرض من اجل الحساب السريع ، ويقطع خطوط العرض عند 85.05 درجة تقريبًا من اجل تقديم مربع. المعيار الفعلي لتطبيقات رسم خرائط الويب.
إسقاط غاوس-كروغر = إسقاط غاوس محافظ= ميركاتور المستعرض (الإهليلجي) 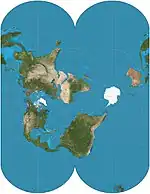أسطواني محافظ كارل فريدريش غاوس

يوهان هينريتش لويس كروغر

 1822 هذا الشكل المستعرض الإهليلجي للمركاتور محدود على عكس المركاتور الاستوائي، و يشكل أساس نظام إحداثيات ميركاتور المستعرض العالمي.
إسقاط سمتي مائل لروسيله هنري روسيله 1922
مركاتور هوتين المائل 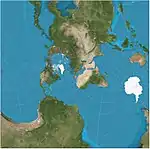أسطواني محافظ م روزنموند ، ج لابورد ، مارتن هوتين 1903
إسقاط غال التجسيمي 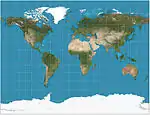أسطواني توفيقي جيمس غال 1855 يُقصد به أن يشبه مركاتور أثناء عرض القطبين أيضًا.

خطوط العرض القياسية عند 45 درجة شمالاً / جنوبًا.

إسقاط ميلر

= ميلرأسطواني

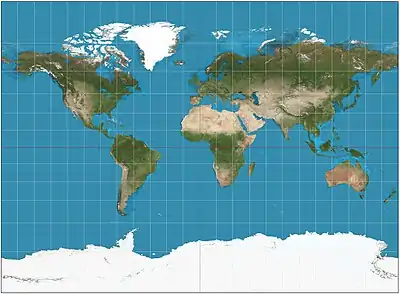أسطواني توفيقي أوسبورن ميتلاند ميلر 1942 يُقصد به أن يشبه مركاتور أثناء عرض القطبين أيضًا.

إسقاط لامبرت الأسطواني متساوي المساحات

 أسطواني متساوي المساحات يوهان هاينغيش لامبرت 1772 خط العرض القياسي عند خط الاستواء. نسبة العرض إلى الارتفاع (π (3.14. الإسقاط الأساسي للعائلة الأسطوانية متساوية المساحات
إسقاط بيرمان 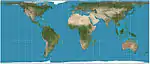أسطواني متساوي المساحات فالتر بيرمان 1910 نسخة مضغوطة أفقيًا من لامبرت متساوي المساحات. لديه خطوط عرض قياسية عند 30 درجة شمالاً / جنوبًا ونسبة عرض إلى ارتفاع تبلغ 2.36.
إسقاط هوبو–داير 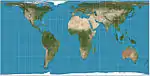أسطواني متساوي المساحات ميك داير Mick Dyer 2002 نسخة مضغوطة أفقيًا من لامبرت متساوي المساحات. متشابه جدًا مع إسقاطي تريستن ادوارد و سميث متساوي المساحات (= مستطيل كراستر). خطوط العرض القياسية عند حوالي 37 درجة شمالاً / جنوبًا. نسبة العرض إلى الارتفاع ~ 2.0.
إسقاط غال-بيترز= غال-بيترز متعامد 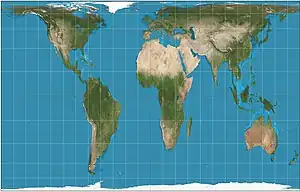أسطواني متساوي المساحات جيمس غال

(أرنو بيترز)

 1855 نسخة مضغوطة أفقيًا من لامبرت متساوي المساحات. خطوط العرض القياسية عند 45 درجة شمالاً / جنوبًا. نسبة العرض إلى الارتفاع ~ 1.6. مشابه لإسقاط بالتزار الذي يمتلك خطوط عرض قياسية عند 50 درجة شمالاً / جنوبًا.
إسقاط أسطواني مركزي أسطواني منظوري

(Perspective)

 (غير معروف) 1850ق. 1850 غير مستخدم عمليا في رسم الخرائط بسبب التشوه القطبي الشديد ، ولكنه شائع في التصوير البانورامي ، خاصة بالنسبة للمشاهد المعمارية.
إسقاط جيبي 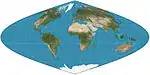شبه أسطواني متساوي المساحات والمسافات (عديدون ؛ الأول غير معروف) 1600ق. 1600 خطوط الطول جيبية. خطوط العرض متباعدة بالتساوي. نسبة العرض إلى الارتفاع 2: 1. يتم الحفاظ على المسافات على طول خطوط العرض.
إسقاط مولفيده 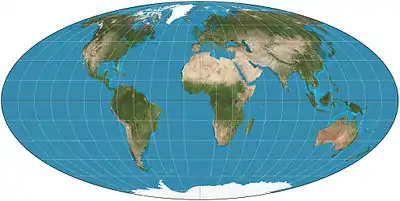شبه أسطواني متساوي المساحات كارل مولفيده 1805 خطوط الطول بيضاوية الشكل
إيكرت 2 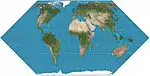شبه أسطواني متساوي المساحات ماكس إيكرت-غرايفيندروف 1906
إيكرت 4 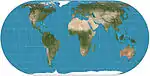شبه أسطواني متساوي المساحات ماكس إيكرت-غرايفيندروف 1906 خطوط العرض غير متساوية التباعد والمقياس ؛ خطوط الطول الخارجية نصف دائرية. باقي خطوط الطول إهليلجية.
إيكرت 6 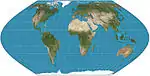شبه أسطواني متساوي المساحات ماكس إيكرت-غرايفيندروف 1906 خطوط العرض غير متساوية التباعد والمقياس ؛ خطوط الطول جيبية نصف دورية.
إسقاط أورتيليوس البيضوي 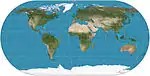شبه أسطواني توفيقي باتيستا أنييزي 1540 خطوط الطول دائرية.[2]
إسقاط غود 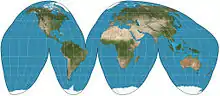شبه أسطواني متساوي المساحات جون بول غود 1923 هجين بين الإسقاط الجيبي وإسقاط مولفيدة.

عادة ما يستخدم في شكل متقطع.

كافرايسكي 7 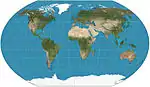شبه أسطواني توفيقي فلاديمير كافرايسكي 1939 خطوط العرض متباعدة بالتساوي. مكافئ لواغنر 6 مضغوطًا أفقيًا بمعامل .
إسقاط روبنسون 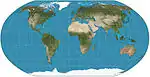شبه أسطواني توفيقي آرثر روبنسون 1963 يحسب باستيفاء القيم المجدولة. استخدمها راند ماكنالي منذ إنشائها واستخدمتها منظمة ناشيونال جيوغرافيك بين 1988-1998.
إسقاط الأرض المتساوية 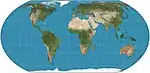شبه أسطواني متساوي المساحات بويان سافريتش ، توم باترسون ، برنارد جيني 2018 مستوحى من إسقاط روبنسون ، لكنه يحتفظ بالحجم النسبي للمناطق.
إسقاط الأرض الطبيعية 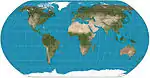شبه أسطواني توفيقي توم باترسون 2011 يحسب باستيفاء القيم المجدولة
توبلر مفرط الإهليلجية 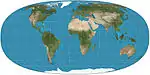شبه أسطواني متساوي المساحات والدو ر. توبلر 1973 عائلة من إسقاطات الخرائط التي تتضمن كحالات خاصة إسقاط مولفيده وإسقاط كوليجنون وعددا من الإسقاطات الأسطوانية متساوية المساحات.
واغنر 6 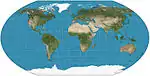شبه أسطواني توفيقي ك. ه. واغنر 1932 مكافئ لكافرايسكي 7 مضغوطًا عموديًا بمعامل .
كوليجنون شبه أسطواني متساوي المساحات إدوارد كوليجنون 1865ق. 1865 حسب الاعدادات ، قد يرسم الإسقاط أيضًا الكرة على ماسة واحدة أو زوج من المربعات.
هيلبيكس 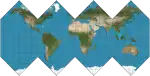شبه أسطواني متساوي المساحات كرزيستوف جورسكي 1997 هجين من كوليجنون + لامبرت أسطواني متساوي المساحات.
بوغز إنحرافي 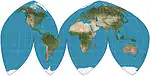شبه أسطواني متساوي المساحات صمويل ويتيمور بوغز 1929 الإسقاط متساوي المساحات الناتج عن متوسط إحداثيات y الجيبي ومولفيده وبالتالي تقييد الإحداثي x.
كراستر شلجمي 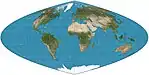شبه أسطواني متساوي المساحات جون كراستر 1929 خطوط الطول هي قطع مكافئ. خطوط العرض القياسية عند الدرجة

36 ° 46 ′ شمال /جنوب   ؛ خطوط العرض غير متساوية في التباعد و المقياس؛ نسبة 2 : 1.

ماكبرايد _توماس

مسطح القطب رباعي

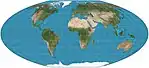شبه أسطواني متساوي المساحات فيليكس ماكبرايد ، بول توماس 1949 خطوط العرض القياسية عند الدرجة 33° 45′ شمال /جنوب  ؛ خطوط العرض غير متكافئة في التباعد والنطاق ؛ خطوط الطول هي منحنيات من الدرجة الرابعة.

خالي من التشويه فقط عندما تتقاطع خطوط العرض القياسية مع خط الزوال الرئيسي.

رباعي متساوي االمساحات 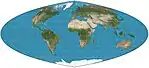شبه أسطواني متساوي المساحات كارل سيمون

اوسكار ادامز

 1937

1944

 خطوط العرض غير متساوية في التباعد والحجم. لا تشويه على طول خط الاستواء. خطوط الطول هي منحنيات من الدرجة الرابعة.
التايمز 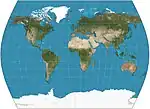شبه أسطواني توفيقي جون موير 1965 خطوط العرض القياسية عند الدرجة 45 شمال /جنوب  . خطوط العرض مثل غال التجسيمي ، ولكن مع خطوط طول منحنية. تم تطويره لصالح شركة Bartholomew Ltd، أطلس التايمز.
لوكسيموثالي 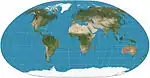شبه أسطواني توفيقي كارل سيمون

والدو توبلر

 1935

1966

 من المركز المُعيّن ، تكون خطوط المحامل الثابتة (خطوط الاتجاه) مستقيمة ولها الطول الصحيح. بشكل عام غير متماثل حول خط الاستواء.
أيتوف 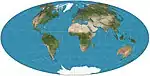شبه سمتي توفيقي ديفيد أيتوف 1889 تمديد للخريطة الاستوائية المعدلة للسمتي متساوي المسافات. الحدود هي 2 : 1 قطع ناقص. حل محله اسقاط هامر بنسبة كبيرة.
هامر 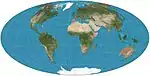شبه سمتي متساوي المساحات ارنست هامر 1892 معدل من الخريطة الاستوائية للسمتي متساوي المساحات. الحدود هي 2 : 1 قطع ناقص. المتغيرات هي نسخ مائلة ، يتمحور حول 45 درجة شمالاً.
ستريب 1995 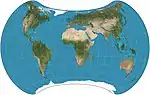شبه سمتي متساوي المساحات دانيال "دان" ستريب 1994 تمت صياغته باستخدام إسقاطات أخرى متساوية المساحات .
وينكل ثلاثي 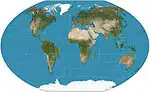شبه سمتي توفيقي أوزوالد وينكل 1921 المتوسط الحسابي للإسقاط متساوي المستطيلات و إسقاط آيتوف. الإسقاط العالمي القياسي لمنظمة ناشيونال جيوغرافيك

منذ عام 1998.

فان دير جرينتن أخرى توفيقي ألفونس فان دير جرينتن 1904 حدوده على شكل دائرة.  خطوط العرض وخطوط الطول هي أقواس دائرية. عادة ما تم قصها بالقرب من 80 درجة شمالاً / جنوبًا. الإسقاط العالمي القياسي لمنظمة ناشيونال جيوغرافيك بين عامي 1922 و 1988.
مخروطي متساوي المسافات= مخروطي بسيط 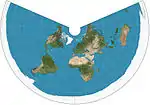مخروطي متساوي المسافات قائم على الإسقاط الأول لبطليموس 100ق. 100 يتم الحفاظ على المسافات بين خطوط الطول ، وكذلك المسافة على طول خط أو اثنين من خطوط العرض القياسية.[3]
لامبرت مخروطي محافظ 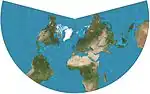مخروطي محافظ يوهان هاينريش لامبرت 1772 يستخدم في الرسوم البيانية للطيران.
ألبرز مخروطي 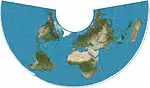مخروطي متساوي المساحات هاينريش ألبرز 1805 خطا عرض قياسيان مع انحراف بسيط بينهما.
إسقاط ويرنر 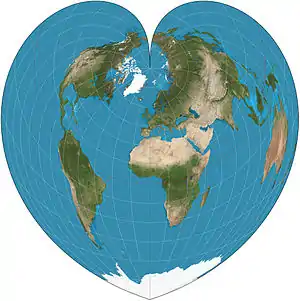شبه مخروطي متساوي المساحات والمسافات يوهانس ستابيوس 1500ق. 1500 خطوط العرض هي أقواس دائرية متحدة المركز متباعدة بشكل متساوٍ. المسافات من القطب الشمالي صحيحة وكذلك المسافات المنحنية على طول خطوط العرض والمسافات على طول خط الزوال الرئيسي.
إسقاط بون 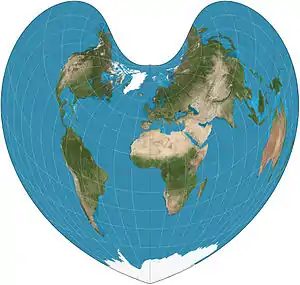شبه مخروطي، قلبي الشكل متساوي المساحات برناردوس سيلفانوس 1511 خطوط العرض هي أقواس دائرية متحدة المركز متباعدة بشكل متساوٍ وخطوط قياسية. المظهر يعتمد على خط العرض المرجعي.

الحالة العامة لاسقاطي واغنر و الجيبي.

بوتوملي 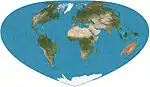شبه مخروطي متساوي المساحات هنري بوتوملي 2003 بديل لإسقاط بون مع شكل عام أبسط؛

خطوط العرض هي أقواس بيضاوية؛

المظهر يعتمد على خط العرض المرجعي.

شبه مخروطي امريكي 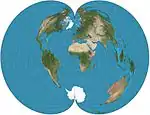شبه مخروطي توفيقي فرديناند رودولف هاسلر 1820ق. 1820 يتم الحفاظ على المسافات على امتداد خطوط العرض وعلى امتداد خط الطول المركزي ايضا.
شبه مخروطي مستطيل  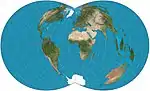 شبه مخروطي توفيقي هيئة المسح الجيوديسي الأمريكية 1853ق. 1853 يمكن اختيار خط العرض الذي يكون المقياس على امتداده صحيحًا. خطوط العرض تلتقي مع خطوط الطول بزوايا قائمة.
شبه مخروطي متساوي التفاوت عرضيا شبه مخروطي توفيقي مكتب الدولة الصيني للمسح ورسم الخرائط 1963 شبه مخروطي : خطوط العرض هي أقواس دوائر غير متحدة المركز.
نيكولوسي كروي 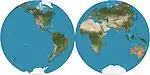شبه مخروطي[4] توفيقي أبو الريحان البيروني؛ أعاد ابتكاره جيوفاني باتيستا نيكولوسي، 1660.[1]:14 1000ق. 1000
إسقاط سمتي متساوي المسافات سمتي متساوي المسافات أبو الريحان البيروني 1000ق. 1000 يتم الحفاظ على المسافات من المركز.

يستخدم كرمز للأمم المتحدة ويمتد حتى 60 درجة جنوباً.

إسقاط مزولي 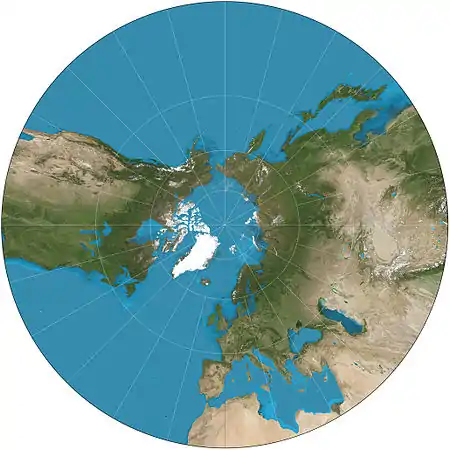سمتي مزولي (Gnomonic) طاليس (محتمل) ق. 580 ق م جميع الدوائر الكبرى ترسم خطوطًا مستقيمة. تشوه شديد بعيدًا عن المركز. يظهر أقل من نصف الكرة الأرضية.
لامبرت سمتي متساوي المساحات 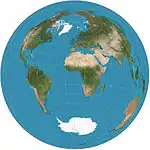سمتي متساوي المساحات يوهان هاينريش لامبرت 1772 مسافة الخط المستقيم بين النقطة المركزية على الخريطة إلى أي نقطة أخرى هي نفس المسافة المستقيمة ثلاثية الأبعاد عبر الكرة الأرضية بين النقطتين.
مجسم 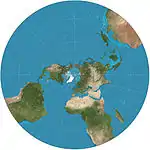سمتي محافظ أبرخش* ق. 200 ق م الخريطة لا نهائية المدى مع تضخم نصف الكرة الخارجي بشدة ، لذلك غالبًا ما تستخدم كنصفين كرويين. تحافظ  جميع  الدوائر الصغيرة على شكلها ، وهو أمر مفيد لرسم الخرائط الكوكبية للحفاظ على أشكال الفوهات الصدمية.
الإسقاط المتعامد سمتي منظوري أبرخش* ق. 200 ق م رؤية من مسافة لا نهائية.
منظور عمودي 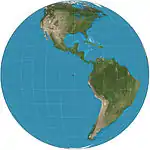سمتي منظوري ماتياس سوتر* 1740 رؤية من مسافة محدودة. يمكنه فقط عرض أقل من نصف الكرة الأرضية.
إسقاط  نقطتان متساويتا البعد سمتي متساوي المسافات هانز مورر 1919 يمكن اختيار "نقطتي تحكم" بشكل عشوائي. مسافتا الخط المستقيم من أي نقطة على الخريطة إلى نقطتي التحكم صحيحتان.
بيرس خماسي 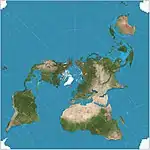أخرى محافظ تشارلز ساندرز بيرس 1879 فسيفسائي. يمكن تبليطه باستمرار على سطح  مستوى ، مع مطابقة تقاطعات الحواف باستثناء أربع نقاط منفردة لكل بلاطة.
إسقاط جويو نصف الكرة في مربع 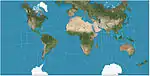أخرى محافظ إميل جويو 1887 فسيفسائي.
إسقاط آدمز نصف الكرة في مربع 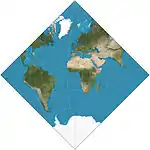أخرى محافظ اوسكار شيرمان ادامز 1925
لي توفيقي رباعي السطوح إسقاط متعدد السطوح

(Polyhedral)

 محافظ إل بي لي 1965 يسقط الكرة الأرضية على رباعي سطوح منتظم. فسيفسائي.
إسقاط اوتاغراف Link to file متعدد السطوح توفيقي هاجيمي ناروكاوا 1999 تقريبًا متساوي المساحات . فسيفسائي.
إسقاط ثماني متعدد السطوح توفيقي ليوناردو دا فينشي 1514 تصور الكرة الأرضية على شكل ثمانية أثمان الدائرة (مثلثات رولو) مع عدم وجود خطوط طول ولا خطوط عرض.
خريطة فراشة لِـكاهيل 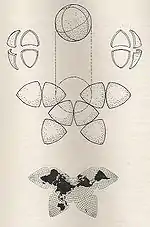متعدد السطوح توفيقي برنارد جوزيف ستانيسلاوس كاهيل 1909 يُسقِط الكرة الأرضية على متعدد سطوح مقطوع بمكونات متناظرة وكتل أرضية متجاورة يمكن عرضها بترتيبات مختلفة.
إسقاط كاهيل-كييز 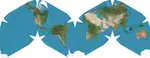متعدد السطوح توفيقي جين كيز 1975 يُسقِط الكرة الأرضية على متعدد سطوح مقطوع بمكونات متناظرة وكتل أرضية متجاورة يمكن عرضها بترتيبات مختلفة.
إسقاط الفراشة لووترمان متعدد السطوح توفيقي ستيف ووترمان 1996 يُسقِط الكرة الأرضية على متعدد سطوح مقطوع بمكونات متناظرة وكتل أرضية متجاورة يمكن عرضها بترتيبات مختلفة.
مكعب كروي رباعي متعدد السطوح متساوي المساحات كينيث ، تشان ، أونيل 1973
اسقاط ديماكسيون متعدد السطوح توفيقي بكمنستر

فولر

 1943 يُعرف أيضًا باسم إسقاط فولر.
كريج سمتي رجعي = مكة 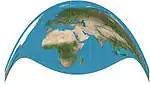سمتي رجعي (Retroazimuthal) توفيقي جيمس ايرلند كريج 1909
هامر سمتي رجعي ، نصف الكرة الأمامي سمتي رجعي ارنست هامر 1910
هامر سمتي رجعي ، نصف الكرة الخلفي سمتي رجعي ارنست هامر 1910
ليترو 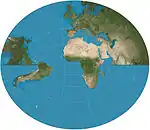سمتي رجعي محافظ جوزيف يوهان ليترو 1833 على الجانب الاستوائي يظهر نصف كروي باستثناء القطبين.
أرماديلو 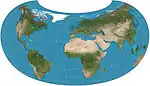أخرى توفيقي اروين رايز 1943
جي اس 50 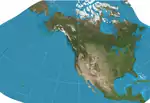أخرى محافظ جون سنايدر 1982 مصمم خصيصًا لتقليل التشوه عند استخدامه لعرض كل الولايات الأمريكية ال50.
واغنر 7

= هامر - واغنر

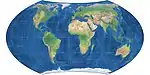 شبه سمتي متساوي المساحات ك واجنر 1941
أطلانطس

= مولفيده مستعرض

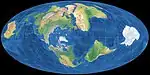 شبه أسطواني متساوي المساحات جون بارثولوميو 1948 نسخة مائلة من مولفيده
بيرتين

= بيرتين -ريفيار = بيرتين 1953

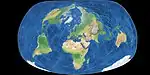 أخرى توفيقي جاك بيرتين 1953 إسقاط حيث لم يعد التوفيق متجانسًا ولكن تم تعديله ليحقق تشوها أكبر للمحيطات و تشوها أقل للقارات. يشيع استخدامه للخرائط الجيوسياسية الفرنسية.[5]

مراجع
  1. Snyder, John P. (1993)، Flattening the earth: two thousand years of map projections، دار نشر جامعة شيكاغو، ص. 1، ISBN 0-226-76746-9.
  2. Donald Fenna (2006)، Cartographic Science: A Compendium of Map Projections, with Derivations، CRC Press، ص. 249، ISBN 978-0-8493-8169-0، مؤرشف من الأصل في 9 أغسطس 2020.
  3. Furuti, Carlos A.، "Conic Projections: Equidistant Conic Projections"، مؤرشف من الأصل في 20 ديسمبر 2013، اطلع عليه بتاريخ 11 فبراير 2020.
  4. "Nicolosi Globular projection" نسخة محفوظة 2016-04-29 على موقع واي باك مشين.
  5. Rivière, Philippe (1 أكتوبر 2017)، "Bertin Projection (1953)"، visionscarto، مؤرشف من الأصل في 27 يناير 2020، اطلع عليه بتاريخ 27 يناير 2020.
  • بوابة جغرافيا
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.