مبرهنة العلم البريطاني

في الهندسة الإقليدية، مبرهنة العلم البريطاني تنص على أنه إذا كانت النقطة P داخل المستطيل ABCD، فإن مجموع مربعَي المسافتين الإقليديتين بين P ورأسين متقابلين في هذا المستطيل، تساوي مجموع مربعي المسافتين بين P والنقطتين الأخريين المتقابلتين.[1][2][3] أي أن: $AP^{2}+CP^{2}=BP^{2}+DP^{2}$ تتحقق المبرهنة أيضاً إذا كانت النقطة P خارج المستطيل ABCD، ويمكن تعميمها إلى أي نقطة في الفضاء الإقليدي.[4]

استناداً إلى مبرهنة العلم البريطاني، فإن المربعين الأحمرين لهما نفس المساحة الإجمالية للمربعين الأزرقين

بصورة عامة، سيكون مجموع مربعي المسافتين بين النقطة P وكل رأسين متاقبلين في متوازي أضلاع على المستوي ذاته مختلفة، لكن الفرق سيعتمد على شكل متوازي الأضلاع، وليس على مكان النقطة P .[5]

البرهان

البرهان

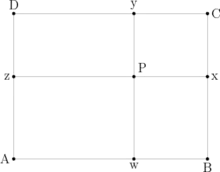
نرسم من النقطة P أعمدة على AB، BC، CD، AD، لتلاقيها في النقاط W، X، Y، Z على الترتيب، كما هو مرسوم على الشكل جانباً، نلاحظ أن WY يعامد XZ، وبتطبيق مبرهنة فيثاغورس ، وبملاحظة أن WP=AZ نجد أن:

$AP^{2}=AW^{2}+WP^{2}=AW^{2}+AZ^{2}$
$PC^{2}=WB^{2}+ZD^{2}$
$BP^{2}=WB^{2}+AZ^{2}$
$PD^{2}=ZD^{2}+AW^{2}$

ومنه: $AP^{2}+PC^{2}=(AW^{2}+AZ^{2})+(WB^{2}+ZD^{2})=(WB^{2}+AZ^{2})+(ZD^{2}+AW^{2})=BP^{2}+PD^{2}.\,$

التسمية

علم المملكة المتحدة بريطانيا.

الاسم مأخوذ من أنه عند رسم القطع المستقيمة الواصلة بين P ورؤوس المستطيل، ورسم الأعمدة من P على الأضلاع، يصبح الشكل الناتج شبيهاً بعلم الاتحاد.

انظر أيضاً

مراجع

Lardner, Dionysius (1848)، The First Six Books of the Elements of Euclid، H.G. Bohn، ص. 87، مؤرشف من الأصل في 26 يناير 2020. Lardner includes this theorem in what he calls "the most useful and remarkable theorems which may be inferred" from the results in Book II of أصول إقليدس.
Young, John Wesley؛ Morgan, Frank Millett (1917)، Elementary Mathematical Analysis، The Macmillan company، ص. 304، مؤرشف من الأصل في 26 يناير 2020.
Bôcher, Maxime (1915)، Plane Analytic Geometry: with introductory chapters on the differential calculus، H. Holt and Company، ص. 17، مؤرشف من الأصل في 26 يناير 2020.
Harvard-MIT Mathematics Tournament solutions^{[وصلة مكسورة]}, Problem 28. "نسخة مؤرشفة" (PDF)، مؤرشف من الأصل في 7 مارس 2007، اطلع عليه بتاريخ 18 أبريل 2016.{{استشهاد ويب}}: صيانة CS1: BOT: original-url status unknown (link)
Hadamard, Jacques (2008)، Lessons in Geometry: Plane geometry، American Mathematical Society، ص. 136، ISBN 978-0-8218-4367-3، مؤرشف من الأصل في 25 سبتمبر 2014.

بوابة رياضيات

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Lardner, Dionysius (1848)، The First Six Books of the Elements of Euclid، H.G. Bohn، ص. 87، مؤرشف من الأصل في 26 يناير 2020. Lardner includes this theorem in what he calls "the most useful and remarkable theorems which may be inferred" from the results in Book II of أصول إقليدس.

[2] Young, John Wesley؛ Morgan, Frank Millett (1917)، Elementary Mathematical Analysis، The Macmillan company، ص. 304، مؤرشف من الأصل في 26 يناير 2020.

[3] Bôcher, Maxime (1915)، Plane Analytic Geometry: with introductory chapters on the differential calculus، H. Holt and Company، ص. 17، مؤرشف من الأصل في 26 يناير 2020.

[4] Harvard-MIT Mathematics Tournament solutions^{[وصلة مكسورة]}, Problem 28. "نسخة مؤرشفة" (PDF)، مؤرشف من الأصل في 7 مارس 2007، اطلع عليه بتاريخ 18 أبريل 2016.{{استشهاد ويب}}: صيانة CS1: BOT: original-url status unknown (link)

[5] Hadamard, Jacques (2008)، Lessons in Geometry: Plane geometry، American Mathematical Society، ص. 136، ISBN 978-0-8218-4367-3، مؤرشف من الأصل في 25 سبتمبر 2014.