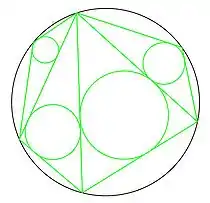
مبرهنة يابانية في مضلع دائري
في الهندسة الرياضية، تنص المبرهنة اليابانية على أنه مهما كان شكل تثليث مضلع دائري، فإن مجموع أنصاف أقطار الدوائر الداخلية للمثلثات يكون ثابتا.[1][2][3]
|
|
|
|
مجموع أنصاف أقطار الدوائر الخضراء = مجموع أنصاف أقطار الدوائر الحمراء | |
وعكس المبرهنة أيضاً صحيح، بحيث إذا كان مجموع أنصاف أقطار الدوائر الداخلية لتثليث معين مستقلاً عن شكل التثليث، فإن المضلع يكون دائرياً.
مراجع
- Fukagawa, Hidetoshi؛ Pedoe, D. (1989)، Japanese Temple Geometry، Manitoba, Canada: Charles Babbage Research Center، ص. 125–128، ISBN 0919611214.
- In search of "Japanese theorem نسخة محفوظة 29 يوليو 2010 على موقع واي باك مشين.
- Reyes, Wilfred (2002)، "An Application of Thébault's Theorem" (PDF)، Forum Geometricorum، 2: 183–185، مؤرشف من الأصل (PDF) في 24 أكتوبر 2018، اطلع عليه بتاريخ 02 سبتمبر 2015.
- بوابة رياضيات
- بوابة هندسة رياضية
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.