مضلع متجانف
مضلع متجانف في الهندسة ، المضلع المنحرف هو مضلع لا تكون رؤوسه كلها متحد المستوى ،يجب أن تحتوي مضلعات الانحراف على أربعة رؤوس على الأقل وتكون المضلعات اللانهائية المنحرفة (apeirogons) لها رؤوس ليست كلها خطية. المضلع المنحرف المتعرج أو المضلع المضاد له رؤوس تتناوب على اثنين مضلعات الانحراف المنتظمة ذات الأبعاد الثلاثة (والمضلعات المنحرفة المنتظمة في بعدين) دائمًا ما تكون متعرجة.
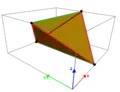
مضلع منحرف مضاد للتجميد في ثلاثة أبعاد
مضلع الانحراف المنتظم متساوي مع أطوال حواف متساوية. في 3 أبعاد ، يكون مضلع الانحراف المنتظم عبارة عن مضلع منحرف متعرج (أو مضاد للتعرج) ، مع تناوب الرؤوس بين مستويين متوازيين. يمكن أن تحدد الحواف الجانبية لـ n-antiprism انحرافًا منتظمًا 2n-gon.
يمكن إعطاء الانحراف العادي n-gon رمز Schläfli {p} # {} كمزيج من مضلع عادي {p} ومقطع خط متعامد {}. [2] عملية التناظر بين القمم المتسلسلة هي انعكاس انحدار.
يتم عرض الأمثلة على التناقضات المربعة والخماسية الشكل. تولد أيضًا مضادات الانحراف النجمية مضلعات منحرفة منتظمة بترتيب اتصال مختلف للمضلعات العلوية والسفلية. يتم رسم المضلعات العلوية والسفلية المعبأة من أجل الوضوح الهيكلي ، وليست جزءًا من مضلعات الانحراف.
| مربع الانحراف | سداسي الانحراف | الانحراف المثمن | انحراف عشري | الانحراف dodecagon | ||
| {2}#{ } | {3}#{ } | {4}#{ } | {5}#{ } | {5/2}#{ } | {5/3}#{ } | {6}#{ } |
 |
 |
 |
 |
 |
 |
 |
| s{2,4} | s{2,6} | s{2,8} | s{2,10} | sr{2,5/2} | s{2,10/3} | s{2,12} |
مضلعات بيتري هي مضلعات منحرفة منتظمة يتم تحديدها داخل متعددات الوجوه العادية ومتعددة السطوح. على سبيل المثال ، تحتوي الأجسام الصلبة الأفلاطونية الخمسة على مضلعات منحرفة منتظمة من 4 و 6 و 10 جوانب ، كما يظهر في هذه الإسقاطات المتعامدة ذات الحواف الحمراء حول المغلفات الإسقاطية الخاصة بها . يشتمل رباعي الوجوه وثماني الوجوه على جميع الرؤوس في مضلعات الانحراف المتعرج الخاصة بكل منهما ، ويمكن رؤيته على أنه مضاد ديجوني وضد مثلث على التوالي.
مضلع منحرف منتظم كرقم رأسي لمتعدد الوجوه المائل المنتظم
إن الانحراف المنتظم متعدد السطوح له أوجه مضلعة منتظمة وشكل رأس مضلع مائل منتظم.
ثلاثة أشكال متعددة الوجوه منتظمة لانهائية تملأ الفراغ في 3 مسافات ؛ البعض الآخر موجود في 4 فضاء ، وبعضها داخل 4-polytopes موحدة.
المضلعات المنحرفة متساوية الأضلاع في ثلاثة أبعاد
مضلع الانحراف المتساوي هو مضلع منحرف بنوع واحد من الرؤوس ، متصل بنوعين من الحواف. يمكن أيضًا اعتبار المضلعات المنحرفة المتساوية ذات أطوال حواف متساوية شبه دائرية. إنه مشابه لمضلع انحراف متعرج ، موجود على مستويين ، باستثناء السماح لحافة واحدة بالعبور إلى المستوى المقابل ، والحافة الأخرى بالبقاء على نفس المستوى.
يمكن تعريف مضلعات الانحراف المتساوي الأضلاع على مناشير n-gonal متساوية الجوانب ، بالتناوب تتبع حافة مضلع جانب واحد ، والتنقل بين المضلعات. على سبيل المثال ، على رؤوس المكعب. تتناوب الرؤوس بين المربعات العلوية والسفلية مع وجود حواف حمراء بين الجوانب وحواف زرقاء على طول كل جانب.
| Octagon | Dodecagon | Icosikaitetragon | ||||
|---|---|---|---|---|---|---|
 مكعب, square-diagonal |
 Cube |
 Crossed cube |
 موشور سداسي |
 Hexagonal prism |
 Hexagonal prism |
 منشور |
مضلعات الانحراف المنتظم بأربعة أبعاد
في 4 أبعاد ، يمكن أن يكون لمضلع الانحراف المنتظم رؤوس على حلق كليفورد ومرتبط بإزاحة كليفورد. على عكس المضلعات المنحرفة المتعرجة ، يمكن أن تتضمن المضلعات المنحرفة في الدورات المزدوجة عددًا فرديًا من الجوانب.
تحدد المضلعات بيتري في الأشكال الأربعة العادية المضلعات المنحرفة المنتظمة المتعرجة. يوضح رقم Coxeter لكل تناظر مجموعة coxeter عدد جوانب مضلع بيتري. هذا هو 5 جوانب لـ 5 خلايا و 8 جوانب لـ tesseract و 16 خلية و 12 جانبًا لـ 24 خلية و 30 جانبًا لـ 120 خلية و 600 خلية.
مراجع
- McMullen, Peter؛ Schulte, Egon (ديسمبر 2002)، Abstract Regular Polytopes (ط. 1st)، مطبعة جامعة كامبريدج، ISBN 0-521-81496-0 p. 25
- قالب:The Geometrical Foundation of Natural Structure (book) "Skew Polygons (Saddle Polygons)" §2.2
- سكوت ماكدونالد كوكستر, H.S.M.; Regular complex polytopes (1974). Chapter 1. Regular polygons, 1.5. Regular polygons in n dimensions, 1.7. Zigzag and antiprismatic polygons, 1.8. Helical polygons. 4.3. Flags and Orthoschemes, 11.3. Petrie polygons
- سكوت ماكدونالد كوكستر, H. S. M. Petrie Polygons. Regular Polytopes, 3rd ed. New York: Dover, 1973. (sec 2.6 Petrie Polygons pp. 24–25, and Chapter 12, pp. 213–235, The generalized Petrie polygon)
- Coxeter, H. S. M. & Moser, W. O. J. (1980)، Generators and Relations for Discrete Groups، New York: Springer-Verlag، ISBN 0-387-09212-9. (1st ed, 1957) 5.2 The Petrie polygon {p,q}.
- جون ملنور: On the total curvature of knots, Ann. Math. 52 (1950) 248–257.
- جون إم. سوليفان: Curves of finite total curvature, ArXiv:math.0606007v2