Constructive solid geometry
Constructive solid geometry (CSG; formerly called computational binary solid geometry) is a technique used in solid modeling. Constructive solid geometry allows a modeler to create a complex surface or object by using Boolean operators to combine simpler objects,[1] potentially generating visually complex objects by combining a few primitive ones.[2][3]
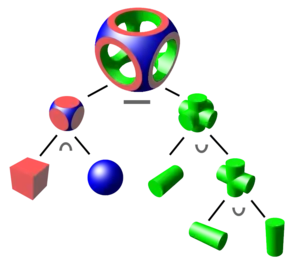
In 3D computer graphics and CAD, CSG is often used in procedural modeling. CSG can also be performed on polygonal meshes, and may or may not be procedural and/or parametric.
Contrast CSG with polygon mesh modeling and box modeling.
Workings
The simplest solid objects used for the representation are called geometric primitives. Typically they are the objects of simple shape: cuboids, cylinders, prisms, pyramids, spheres, cones.[1] The set of allowable primitives is limited by each software package. Some software packages allow CSG on curved objects while other packages do not.
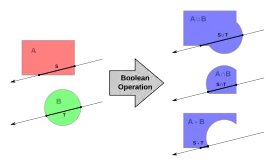
An object is constructed from primitives by means of allowable operations, which are typically Boolean operations on sets: union, intersection and difference, as well as geometric transformations of those sets.[1]
A primitive can typically be described by a procedure which accepts some number of parameters; for example, a sphere may be described by the coordinates of its center point, along with a radius value. These primitives can be combined into compound objects using operations like these:
 Union
Union
Merger of two objects into one Difference
Difference
Subtraction of one object from another Intersection
Intersection
Portion common to both objects
Combining these elementary operations, it is possible to build up objects with high complexity starting from simple ones.
Ray tracing
Rendering of constructive solid geometry is particularly simple when ray tracing. Ray tracers intersect a ray with both primitives that are being operated on, apply the operator to the intersection intervals along the 1D ray, and then take the point closest to the camera along the ray as being the result.
Applications
Constructive solid geometry has a number of practical uses. It is used in cases where simple geometric objects are desired, or where mathematical accuracy is important.[4] Nearly all engineering CAD packages use CSG (where it may be useful for representing tool cuts, and features where parts must fit together).
The Quake engine and Unreal Engine both use this system, as does Hammer (the native Source engine level editor), and Torque Game Engine/Torque Game Engine Advanced. CSG is popular because a modeler can use a set of relatively simple objects to create very complicated geometry.[3] When CSG is procedural or parametric, the user can revise their complex geometry by changing the position of objects or by changing the Boolean operation used to combine those objects.
One of the advantages of CSG is that it can easily assure that objects are "solid" or water-tight if all of the primitive shapes are water-tight.[5] This can be important for some manufacturing or engineering computation applications. By comparison, when creating geometry based upon boundary representations, additional topological data is required, or consistency checks must be performed to assure that the given boundary description specifies a valid solid object.[1]
A convenient property of CSG shapes is that it is easy to classify arbitrary points as being either inside or outside the shape created by CSG. The point is simply classified against all the underlying primitives and the resulting boolean expression is evaluated.[6] This is a desirable quality for some applications such as ray tracing.[6]
Conversion from meshes to CSG
With CSG models being parameterized by construction, they are often favorable over usual meshes when it comes to applications where the goal is to fabricate customized models. For such applications it can be interesting to convert already existing meshes to CSG trees. This problem of automatically converting meshes to CSG trees is called inverse CSG.
A resulting CSG tree is required to occupy the same volume in 3D space as the input mesh while having a minimal number of nodes. Simple solutions are preferred to ensure that the resulting model is easy to edit. Solving this problem is a challenge because of the large search space that has to be explored. It combines continuous parameters such as dimension and size of the primitive shapes, and discrete parameters such as the Boolean operators used to build the final CSG tree.
Deductive methods solve this problem by building a set of half-spaces that describe the interior of the geometry. These half-spaces are used to describe primitives that can be combined to get the final model.[7]
Another approach decouples the detection of primitive shapes and the computation of the CSG tree that defines the final model. This approach exploits the ability of modern program synthesis tools to find a CSG tree with minimal complexity.[8]
There are also approaches that use genetic algorithms to iteratively optimize an initial shape towards the shape of the desired mesh.[9]
Notable applications with CSG support
Ray tracing and particle transport
Computer-aided design
Gaming
- Dreams
- Godot[10]
- GtkRadiant
- Unity, via free or paid plug-ins from the Unity Asset Store.
- UnrealEd
- Valve Hammer Editor
- Roblox
References
- Foley, James D. (1996), "12.7 Constructive Solid Geometry", Computer Graphics: Principles and Practice, Addison-Wesley Professional, pp. 557–558, ISBN 9780201848403,
- Roth, Scott (1982). "Ray Casting for Modeling Solids". Computer Graphics and Image Processing. 18 (2): 109–144. doi:10.1016/0146-664X(82)90169-1.
- Bloomenthal, Jules; Bajaj, Chandrajit (1997), "5.2.5 Intersection with CSG Trees", Introduction to Implicit Surfaces, Morgan Kaufmann, pp. 178–180, ISBN 9781558602335.
- Foley (1996), p. 559.
- van Rossen, Sander; Baranowski, Matthew (2011), "Real-time constructive solid geometry", in Ansari, Marwan (ed.), Game Development Tools, CRC Press, pp. 79–96, ISBN 9781439867723.
- Glassner, Andrew S. (1989), An Introduction to Ray Tracing, Morgan Kaufmann, p. 80, ISBN 9780122861604.
- Buchele, Suzanne F.; Crawford, Richard H. (2004). "Three-dimensional halfspace constructive solid geometry tree construction from implicit boundary representations". Computer-Aided Design. 36 (11): 1063–1073. doi:10.1016/j.cad.2004.01.006.
- Du, Tao; Inala, Jeevana Priya; Pu, Yewen; Spielberg, Andrew; Schulz, Adriana; Rus, Daniela; Solar-Lezama, Armando; Matusik, Wojciech (2018). "InverseCSG: automatic conversion of 3D models to CSG trees". ACM Trans. Graph. doi:10.1145/3272127.3275006.
- Fayolle, Pierre-Alain; Pasko, Alexander A. (2016). "An evolutionary approach to the extraction of object construction trees from 3D point clouds" (PDF). Computer-Aided Design. 74: 1–17. doi:10.1016/j.cad.2016.01.001.
- Godot Engine - Godot gets CSG support
- Gregory, Paul (February 12, 2002). "Major release". Retrieved May 20, 2020 – via SourceForge.