Cuboid

In geometry, a cuboid is a hexahedron, a six-faced solid. Its faces are quadrilaterals. Cuboid means "like a cube", in the sense that by adjusting the lengths of the edges or the angles between faces, a cuboid can be transformed into a cube. In mathematical language a cuboid is a convex polyhedron whose polyhedral graph is the same as that of a cube.

For other uses, see Cuboid (disambiguation).

A special case of a cuboid is a rectangular cuboid, with six rectangles as faces and adjacent faces meeting at right angles. A cube is a special case of a rectangular cuboid, with six square faces meeting at right angles.[1][2]

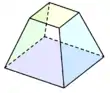
By Euler's formula the numbers of faces F, of vertices V, and of edges E of any convex polyhedron are related by the formula F + V = E + 2. In the case of a cuboid this gives 6 + 8  = 12 + 2; that is, like a cube, a cuboid has six faces, eight vertices, and twelve edges. Along with the rectangular cuboids, any parallelepiped is a cuboid of this type, as is a square frustum (the shape formed by truncation of the apex of a square pyramid).

Quadrilaterally-faced hexahedron (cuboid) 6 faces, 12 edges, 8 vertices
Cube
(square)		 Rectangular cuboid
(three pairs of
rectangles)		 Trigonal trapezohedron
(congruent rhombi)		 Trigonal trapezohedron
(congruent quadrilaterals)		 Quadrilateral frustum
(apex-truncated
square pyramid)		 Parallelepiped
(three pairs of
parallelograms)		 Rhombohedron
(three pairs of
rhombi)
Oh, [4,3], (*432)
order 48		 D2h, [2,2], (*222)
order 8		 D3d, [2+,6], (2*3)
order 12		 D3, [2,3]+, (223)
order 6		 C4v, [4], (*44)
order 8		 Ci, [2+,2+], (×)
order 2

See also

References
  1. Robertson, Stewart Alexander (1984). Polytopes and Symmetry. Cambridge University Press. p. 75. ISBN 9780521277396.
  2. Dupuis, Nathan Fellowes (1893). Elements of Synthetic Solid Geometry. Macmillan. p. 53. Retrieved December 1, 2018.
Wikimedia Commons has media related to Hexahedra with cube topology.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.