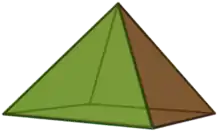
Square pyramid
In geometry, a square pyramid is a pyramid that has five faces, including four triangles and one square as the base. If its apex is perpendicularly above the center of the base, it is a right square pyramid that has four isosceles triangles; otherwise, it is an oblique square pyramid. When all the edges have the same length, the four triangular faces become equilateral, and therefore it forms an equilateral square pyramid.
| Square pyramid | |
|---|---|
 | |
| Type | Johnson J92 – J1 – J2 |
| Faces | 4 triangles 1 square |
| Edges | 8 |
| Vertices | 5 |
| Vertex configuration | 4 (32.4) (34)[1] |
| Symmetry group | C4v |
| Volume | |
| Dual polyhedron | self-dual |
| Properties | convex |
| Net | |
 | |

A square pyramid can be used in architecture, and an example of a building that resembles the shape is Egyptian pyramid. It can also be used in chemistry as a molecular structure, a square pyramidal molecular. Aside from those applications, a square pyramid can be used for constructing a polyhedron.
Properties
Right and equilateral square pyramid
A square pyramid has eight edges, five faces that include four triangles, and one square as the base.[2] It also has five vertices, one of which is an apex, a vertex where all lateral edges meet.[3] A lateral edge is a segment line between the apex and another vertex at the square base.[4] When the apex is perpendicularly above the center of the base, all the lateral edges have the same length, and the faces other than the base are congruent isosceles triangles, a right square pyramid. A square pyramid where the apex is not perpendicularly above the center of the base, and the faces are not an isosceles triangle is an oblique square pyramid.[5]
When all edges have the same length, the four isosceles triangles become equilateral, and therefore all the faces are regular polygons. This pyramid is known as an equilateral square pyramid.[6] Its dihedral angle between two adjacent triangular faces and between the base and triangular face is
respectively. It has three-dimensional symmetry group of cyclic group pyramidal symmetry, a symmetry of order eight; this means that it is symmetrical as one rotates it for every quarter-turn of a full angle around the axis of symmetry, two vertical planes passing through the diagonals of the square base, and two other vertical planes passing through the midpoint of the opposite edges of the square base.[1] A convex polyhedra that has regular polygons as its faces is called Johnson solid, and because an equilateral square pyramid has these properties, it is a Johnson solid that numbered as among them.[7]
Surface area and volume
The slant of a right square pyramid can be considered as the height of an isosceles triangle, which can be obtained by applying the Pythagorean theorem, that is:[8]
Here, is the length of the base of an isosceles triangle, and is the length of the side of an isosceles triangle, a lateral edge of a right square pyramid.[8][9] The height of a right square pyramid can be considered and obtained similarly, and substitute the formula of the slant gives[8]
A surface area is the total area of the faces of a polyhedron. Hence, the surface area of a square pyramid can be expressed as the sum of four times the area of a triangle and the area of a square. The area of a triangle is the half product of the base and side, and the area of a square is the second power of its side. This can be formulated as:[10]
The volume of a pyramid, in general, is given by one-third of the product of the area of the base and the height.[11] As for the pyramid with a square base, the formula can be expressed as:[12]
Applications

In architecture, an example of a building that resembles a square pyramid is Egyptian pyramid.[2] In Moscow Mathematical Papyrus, the ancient Egyptians already knew the formula for calculating the volume of a truncated square pyramid. One can conclude that they were already acquainted with the volume of a square pyramid, but it is unknown how the formula was attested. The problem of finding the slope and height of a square pyramid can be found in the Rhind Mathematical Papyrus.[13] Another building that has the structure of a square pyramid is Louvre Pyramid and a casino hotel Luxor Las Vegas.[14][15]
In stereochemistry, a square pyramid can be described as the cluster of a square pyramidal molecular geometry. The square pyramidal molecule is the main-group element that has one active lone pair, which can be described by VSEPR theory, a model to predict the arrangement of the number of electron pairs around central atoms in molecules.[16] Some examples of a cluster based on that structure are chlorine pentafluoride, bromine pentafluoride, and iodine pentafluoride.[17]
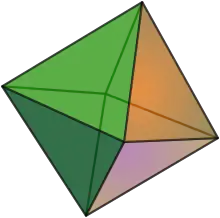
A square pyramid can be used to construct a new polyhedron by attaching its base onto the square face of another polyhedron, a process known as augmentation. In general, it is a process of attaching the pyramid, cupolae, and rotunda to another polyhedron; specifically, a process of attaching them to a prism and an antiprism are known as elongation and gyroelongation, respectively.[18] An example of this construction is an octahedron (or a square bipyramid), which can be constructed by attaching the base of two square pyramids.[19] Another polyhedron is a tetrakis hexahedron, which can be constructed by putting the base of six equilateral square pyramids onto the faces of a cube.[20] In addition to those polyhedrons, some Johnson solids can be constructed by attaching the base of some square pyramids as well, that is: elongated square pyramid , gyroelongated square pyramid , elongated square bipyramid , gyroelongated square bipyramid , augmented triangular prism , biaugmented triangular prism , triaugmented triangular prism , augmented pentagonal prism , biaugmented pentagonal prism , augmented hexagonal prism , parabiaugmented hexagonal prism , metabiaugmented hexagonal prism , triaugmented hexagonal prism , and augmented sphenocorona .[21]
See also
- Square pyramidal number, a natural number that counts the number of stacked spheres in a square pyramid.
References
- Johnson, Norman W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. MR 0185507. S2CID 122006114. Zbl 0132.14603. See table III, line 1.
- Kinsey, L. Christine; Moore, Teresa E.; Prassidis, Efstratios (2011). Geometry and Symmetry. John Wiley & Sons. p. 371. ISBN 978-0-470-49949-8.
- O'Keeffe, Michael; Hyde, Bruce G. (2020). Crystal Structures: Patterns and Symmetry. Dover Publications. p. 141. ISBN 9780486836546.
- Smith, James T. (2000). Methods of Geometry. John Wiley & Sons. p. 98. ISBN 0-471-25183-6.
- Freitag, Mark A. (2014). Mathematics for Elementary School Teachers: A Process Approach. Brooks/Cole. p. 598. ISBN 978-0-618-61008-2.
- Hocevar, Franx (1903). Solid Geometry. A. & C. Black. p. 44.
- Uehara, Ryuhei (2020). Introduction to Computational Origami: The World of New Computational Geometry. Springer. p. 62. doi:10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5.
- Larcombe, H. J. (1929). Cambridge Intermediate Mathematics: Geometry Part II. Cambridge University Press. p. 177.
- Perry, O. W.; Perry, J. (1981). Mathematics. Springer. pp. 145–146. doi:10.1007/978-1-349-05230-1. ISBN 978-1-349-05230-1.
- Freitag (2014), p. 798.
- Alexander, Daniel C.; Koeberlin, Geralyn M. (2014). Elementary Geometry for College Students (6th ed.). Cengage Learning. p. 403. ISBN 978-1-285-19569-8.
- Larcombe (1929), p. 178.
- Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. pp. 20–22.
- Jarvis, Daniel; Naested, Irene (2012). Exploring the Math and Art Connection: Teaching and Learning Between the Lines. Brush Education. p. 172. ISBN 978-1-55059-398-3.
- Simonson, Shai (2011). Rediscovering Mathematics: You Do the Math. Mathematical Association of America. p. 154. ISBN 978-0-88385-912-4.
- Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey (2002). General Chemistry: Principles and Modern Applications. Vol. 1. Prentice Hall. p. 414. ISBN 9780130143297.
- Emeléus, H. J. (1969). The Chemistry of Fluorine and Its Compounds. Academic Press. p. 13. ISBN 9781483273044.
- Slobodan, Mišić; Obradović, Marija; Ðukanović, Gordana (2015). "Composite Concave Cupolae as Geometric and Architectural Forms" (PDF). Journal for Geometry and Graphics. 19 (1): 79–91.
- Trigg, Charles W. (1978). "An infinite class of deltahedra". Mathematics Magazine. 51 (1): 55–57. doi:10.1080/0025570X.1978.11976675. JSTOR 2689647. MR 1572246.
- Demey, Lorenz; Smessaert, Hans (2017). "Logical and Geometrical Distance in Polyhedral Aristotelian Diagrams in Knowledge Representation". Symmetry. 9 (10): 204. doi:10.3390/sym9100204.
- Rajwade, A. R. (2001). Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem. Texts and Readings in Mathematics. Hindustan Book Agency. pp. 84–88. doi:10.1007/978-93-86279-06-4. ISBN 978-93-86279-06-4. See Table 12.3, where denotes the -sided prism and denotes the -sided antiprism.
External links
- Weisstein, Eric W., "Square pyramid" ("Johnson solid") at MathWorld.
- Weisstein, Eric W. "Wheel graph". MathWorld.
- Square Pyramid – Interactive Polyhedron Model
- Virtual Reality Polyhedra georgehart.com: The Encyclopedia of Polyhedra (VRML model)