Elongated triangular bipyramid
In geometry, the elongated triangular bipyramid (or dipyramid) or triakis triangular prism is one of the Johnson solids (J14), convex polyhedra whose faces are regular polygons. As the name suggests, it can be constructed by elongating a triangular bipyramid (J12) by inserting a triangular prism between its congruent halves.
| Elongated triangular bipyramid | |
|---|---|
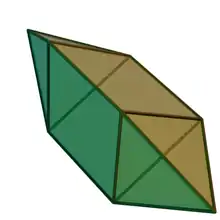 | |
| Type | Johnson J13 – J14 – J15 |
| Faces | 6 triangles 3 squares |
| Edges | 15 |
| Vertices | 8 |
| Vertex configuration | 2(33) 6(32.42) |
| Symmetry group | D3h, [3,2], (*322) |
| Rotation group | D3, [3,2]+, (322) |
| Dual polyhedron | Triangular bifrustum |
| Properties | convex |
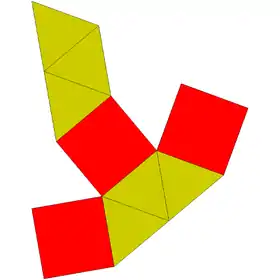
| Net | |
 | |

A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.[1]
The nirrosula, an African musical instrument woven out of strips of plant leaves, is made in the form of a series of elongated bipyramids with non-equilateral triangles as the faces of their end caps.[2]
Formulae
The following formulae for volume (), surface area () and height () can be used if all faces are regular, with edge length a:
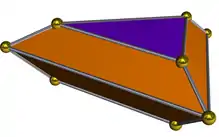
Dual polyhedron
The dual of the elongated triangular bipyramid is called a triangular bifrustum and has 8 faces: 6 trapezoidal and 2 triangular.
| Dual elongated triangular bipyramid | Net of dual |
|---|---|
 |
 |
References
- Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.
- Gerdes, Paulus (2009), "Exploration of technologies, emerging from African cultural practices, in mathematics (teacher) education", ZDM Mathematics Education, 42 (1): 11–17, doi:10.1007/s11858-009-0208-2, S2CID 122791717.
- Stephen Wolfram, "Elongated triangular dipyramid" from Wolfram Alpha. Retrieved July 22, 2010.
- Sapiña, R. "Area and volume of the Johnson solid J14". Problemas y Ecuaciones (in Spanish). ISSN 2659-9899. Retrieved 2020-09-04.