Hyperrectangle
In geometry, an hyperrectangle (also called a box, hyperbox, or orthotope[2]), is the generalization of a rectangle (a plane figure) and the rectangular cuboid (a solid figure) to higher dimensions. A necessary and sufficient condition is that it is congruent to the Cartesian product of finite intervals. If all of the edges are equal length, it is a hypercube. A hyperrectangle is a special case of a parallelotope.
| Hyperrectangle Orthotope | |
|---|---|
 A rectangular cuboid is a 3-orthotope | |
| Type | Prism |
| Facets | 2n |
| Edges | n×2n-1 |
| Vertices | 2n |
| Schläfli symbol | {}×{}×···×{} = {}n[1] |
| Coxeter-Dynkin diagram | |
| Symmetry group | [2n−1], order 2n |
| Dual | Rectangular n-fusil |
| Properties | convex, zonohedron, isogonal |
Types
A four-dimensional orthotope is likely a hypercuboid.
The special case of an n-dimensional orthotope where all edges have equal length is the n-cube or hypercube.[2]
By analogy, the term "hyperrectangle" can refer to Cartesian products of orthogonal intervals of other kinds, such as ranges of keys in database theory or ranges of integers, rather than real numbers.[3]
Dual polytope
| n-fusil | |
|---|---|
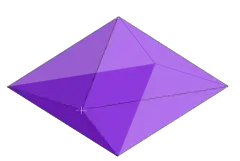 Example: 3-fusil | |
| Facets | 2n |
| Vertices | 2n |
| Schläfli symbol | {}+{}+···+{} = n{}[1] |
| Coxeter-Dynkin diagram | |
| Symmetry group | [2n−1], order 2n |
| Dual | n-orthotope |
| Properties | convex, isotopal |
The dual polytope of an n-orthotope has been variously called a rectangular n-orthoplex, rhombic n-fusil, or n-lozenge. It is constructed by 2n points located in the center of the orthotope rectangular faces.
An n-fusil's Schläfli symbol can be represented by a sum of n orthogonal line segments: { } + { } + ... + { } or n{ }.
A 1-fusil is a line segment. A 2-fusil is a rhombus. Its plane cross selections in all pairs of axes are rhombi.
| n | Example image |
|---|---|
| 1 | { } |
| 2 | .png.webp) { } + { } = 2{ } |
| 3 |  Rhombic 3-orthoplex inside 3-orthotope { } + { } + { } = 3{ } |
See also
Notes
- N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.5 Spherical Coxeter groups, p.251
- Coxeter, 1973
- See e.g. Zhang, Yi; Munagala, Kamesh; Yang, Jun (2011), "Storing matrices on disk: Theory and practice revisited" (PDF), Proc. VLDB, 4 (11): 1075–1086.
References
- Coxeter, Harold Scott MacDonald (1973). Regular Polytopes (3rd ed.). New York: Dover. pp. 122–123. ISBN 0-486-61480-8.
