Coherent addition
Coherent addition (or coherent combining) of lasers is a method of power scaling. It allows increasing the output power and brightness of single-transversal mode laser.
Usually, the term coherent addition applies to fiber lasers. As the ability of pumping and/or cooling of a single laser is saturated, several similar lasers can be forced to oscillate in phase with a common coupler. The first nonlinear theory of the coherent addition of laser sets had been developed by Nikolay Basov with co-workers in 1965. [1] The coherent addition was demonstrated in power scaling of Raman lasers.[2]
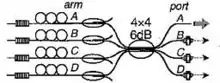
Limits of coherent addition
The addition of lasers reduces the number of longitudinal modes in the output beam; the more lasers are combined, the smaller is the number of longitudinal modes in the output. The simple estimates show that the number of output modes reduces exponentially with the number of lasers combined. Of order of eight lasers can be combined in such a way.[3] The future increase of number of combined lasers requires the exponential growth of the spectral bandwidth of gain and/or length of partial lasers. The same conclusion can be made also on the base of more detailed simulations. [4] Practically, the combination of more than ten lasers with a passive combining arrangement appears to be difficult. However, active coherent combining of lasers has the potential to scale to very large numbers of channels.[5]
Nonlinear coherent addition of lasers
Nonlinear interactions of light waves are used widely to synchronize the laser beams in multichannel optical systems. Self-adjusting of phases may be robustly achievable in binary-tree array of beam-splitters and degenerate four-wave mixing Kerr Phase conjugation[6] in Chirped pulse amplification extreme light facilities.[7] This phase-conjugating Michelson interferometer increases the brightness as ,[8] where is the number of phase-locked channels.
Talbot coherent addition
Constructive interference due to Talbot self-imaging forces the lasers in the array to transverse mode locking. The Fresnel number of the one-dimensional element laser array phase-locked by Talbot cavity is given by[9] For the two-dimensional element laser array phase-locked by Talbot cavity Fresnel number scales as as well. Talbot phase-locking techniques are applicable to thin disk diode-pumped solid-state laser arrays.[10]
See also
References
- Basov, NG; Belenov, EM; Letokhov, VS (1965). "Diffraction synchronization of lasers". Sov. Phys.-Tech. Phys. 10 (2): 845. doi:10.1117/12.160374. S2CID 110333595.
- A. Shirakawa, T. Saitou, T. Sekiguchi and K. Ueda: "Coherent addition of fiber lasers by use of a fiber coupler" Optics Express 10 (2002) 1167–1172
- D. Kouznetsov, J.F. Bisson. A. Shirakawa, K.Ueda "Limits of Coherent Addition of Lasers: Simple Estimate Archived 2007-09-27 at the Wayback Machine" Optical Review Vol. 12, No. 6, 445–447 (2005). (Also .)
- A.E.Siegman. Resonant modes of linearly coupled multiple fiber laser structures. Preprint of the Stanford University, 2005, 25 pages; http://www.stanford.edu/~siegman/coupled_fiber_modes.pdf
- Leo A. Siiman, Wei-zung Chang, Tong Zhou, and Almantas Galvanauskas, "Coherent femtosecond pulse combining of multiple parallel chirped pulse fiber amplifiers" Optics Express 20 (2012) 18097-18116
- Okulov, A Yu (2014). "Coherent chirped pulse laser network with Mickelson phase conjugator". Applied Optics. 53 (11): 2302–2311. arXiv:1311.6703. Bibcode:2014ApOpt..53.2302O. doi:10.1364/AO.53.002302. PMID 24787398. S2CID 118343729.
- "The Nobel Prize in Physics 2018". Nobel Foundation. Retrieved 2 October 2018.
- Basov, N G; Zubarev, I G; Mironov, A B; Michailov, S I; Okulov, A Yu (1980). "Laser interferometer with wavefront reversing mirrors". Sov. Phys. JETP. 52 (5): 847. Bibcode:1980ZhETF..79.1678B.
- Okulov, A Yu (1990). "Two-dimensional periodic structures in nonlinear resonator". JOSA B. 7 (6): 1045–1050. Bibcode:1990JOSAB...7.1045O. doi:10.1364/JOSAB.7.001045.
- Okulov, A Yu (1993). "Scaling of diode-array-pumped solid-state lasers via self-imaging". Opt. Commun. 99 (5–6): 350–354. Bibcode:1993OptCo..99..350O. doi:10.1016/0030-4018(93)90342-3.