Convex analysis

Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory.

A 3-dimensional convex polytope. Convex analysis includes not only the study of convex subsets of Euclidean spaces but also the study of convex functions on abstract spaces.

Convex sets

A subset $C\subseteq X$ of some vector space $X$ is convex if it satisfies any of the following equivalent conditions:

If $0\leq r\leq 1$ is real and $x,y\in C$ then $rx+(1-r)y\in C.$ [1]
If $0<r<1$ is real and $x,y\in C$ with $x\neq y,$ then $rx+(1-r)y\in C.$

Convex function on an interval.

Throughout, $f:X\to [-\infty ,\infty ]$ will be a map valued in the extended real numbers $[-\infty ,\infty ]=\mathbb {R} \cup \{\pm \infty \}$ with a domain $\operatorname {domain} f=X$ that is a convex subset of some vector space. The map $f:X\to [-\infty ,\infty ]$ is a convex function if

f(rx+(1-r)y)\leq rf(x)+(1-r)f(y)

(Convexity ≤)

holds for any real $0<r<1$ and any $x,y\in X$ with $x\neq y.$ If this remains true of $f$ when the defining inequality (Convexity ≤) is replaced by the strict inequality

f(rx+(1-r)y)<rf(x)+(1-r)f(y)

(Convexity <)

then $f$ is called strictly convex.[1]

Convex functions are related to convex sets. Specifically, the function $f$ is convex if and only if its epigraph

A function (in black) is convex if and only if its epigraph, which is the region above its graph (in green), is a convex set.

A graph of the bivariate convex function

x^{2}+xy+y^{2}.

\operatorname {epi} f:=\left\{(x,r)\in X\times \mathbb {R} ~:~f(x)\leq r\right\}

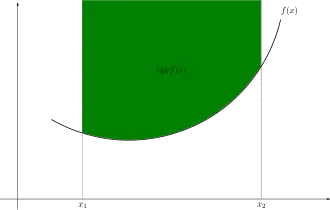
(Epigraph def.)

is a convex set.[2] The epigraphs of extended real-valued functions play a role in convex analysis that is analogous to the role played by graphs of real-valued function in real analysis. Specifically, the epigraph of an extended real-valued function provides geometric intuition that can be used to help formula or prove conjectures.

The domain of a function $f:X\to [-\infty ,\infty ]$ is denoted by $\operatorname {domain} f$ while its effective domain is the set[2]

\operatorname {dom} f:=\{x\in X~:~f(x)<\infty \}.

(dom f def.)

The function $f:X\to [-\infty ,\infty ]$ is called proper if $\operatorname {dom} f\neq \varnothing$ and $f(x)>-\infty$ for all $x\in \operatorname {domain} f.$ [2] Alternatively, this means that there exists some $x$ in the domain of $f$ at which $f(x)\in \mathbb {R}$ and $f$ is also never equal to $-\infty .$ In words, a function is proper if its domain is not empty, it never takes on the value $-\infty ,$ and it also is not identically equal to $+\infty .$ If $f:\mathbb {R} ^{n}\to [-\infty ,\infty ]$ is a proper convex function then there exist some vector $b\in \mathbb {R} ^{n}$ and some $r\in \mathbb {R}$ such that

f(x)\geq x\cdot b-r

for every

x

where $x\cdot b$ denotes the dot product of these vectors.

Convex conjugate

The convex conjugate of an extended real-valued function $f:X\to [-\infty ,\infty ]$ (not necessarily convex) is the function $f^{*}:X^{*}\to [-\infty ,\infty ]$ from the (continuous) dual space $X^{*}$ of $X,$ and[3]

f^{*}\left(x^{*}\right)=\sup _{z\in X}\left\{\left\langle x^{*},z\right\rangle -f(z)\right\}

where the brackets $\left\langle \cdot ,\cdot \right\rangle$ denote the canonical duality ${\displaystyle \left\langle x^{*},z\right\rangle$ The biconjugate of $f$ is the map $f^{**}=\left(f^{*}\right)^{*}:X\to [-\infty ,\infty ]$ defined by $f^{**}(x):=\sup _{z^{*}\in X^{*}}\left\{\left\langle x,z^{*}\right\rangle -f\left(z^{*}\right)\right\}$ for every $x\in X.$ If $\operatorname {Func} (X;Y)$ denotes the set of $Y$ -valued functions on $X,$ then the map $\operatorname {Func} (X;[-\infty ,\infty ])\to \operatorname {Func} \left(X^{*};[-\infty ,\infty ]\right)$ defined by $f\mapsto f^{*}$ is called the Legendre-Fenchel transform.

Subdifferential set and the Fenchel-Young inequality

If $f:X\to [-\infty ,\infty ]$ and $x\in X$ then the subdifferential set is

{\begin{alignedat}{4}\partial f(x):&=\left\{x^{*}\in X^{*}~:~f(z)\geq f(x)+\left\langle x^{*},z-x\right\rangle {\text{ for all }}z\in X\right\}&&({\text{“}}z\in X{\text{''}}{\text{ can be replaced with: }}{\text{“}}z\in X{\text{ such that }}z\neq x{\text{''}})\\&=\left\{x^{*}\in X^{*}~:~\left\langle x^{*},x\right\rangle -f(x)\geq \left\langle x^{*},z\right\rangle -f(z){\text{ for all }}z\in X\right\}&&\\&=\left\{x^{*}\in X^{*}~:~\left\langle x^{*},x\right\rangle -f(x)\geq \sup _{z\in X}\left\langle x^{*},z\right\rangle -f(z)\right\}&&{\text{ The right hand side is }}f^{*}\left(x^{*}\right)\\&=\left\{x^{*}\in X^{*}~:~\left\langle x^{*},x\right\rangle -f(x)=f^{*}\left(x^{*}\right)\right\}&&{\text{ Taking }}z:=x{\text{ in the }}\sup {}{\text{ gives the inequality }}\leq .\\\end{alignedat}}

For example, in the important special case where $f=\|\cdot \|$ is a norm on $X$ , it can be shown[proof 1] that if $0\neq x\in X$ then this definition reduces down to:

\partial f(x)=\left\{x^{*}\in X^{*}~:~\left\langle x^{*},x\right\rangle =\|x\|{\text{ and }}\left\|x^{*}\right\|=1\right\}

and

\partial f(0)=\left\{x^{*}\in X^{*}~:~\left\|x^{*}\right\|\leq 1\right\}.

For any $x\in X$ and $x^{*}\in X^{*},$ $f(x)+f^{*}\left(x^{*}\right)\geq \left\langle x^{*},x\right\rangle ,$ which is called the Fenchel-Young inequality. This inequality is an equality (i.e. $f(x)+f^{*}\left(x^{*}\right)=\left\langle x^{*},x\right\rangle$ ) if and only if $x^{*}\in \partial f(x).$ It is in this way that the subdifferential set $\partial f(x)$ is directly related to the convex conjugate $f^{*}\left(x^{*}\right).$

Biconjugate

The biconjugate of a function $f:X\to [-\infty ,\infty ]$ is the conjugate of the conjugate, typically written as $f^{**}:X\to [-\infty ,\infty ].$ The biconjugate is useful for showing when strong or weak duality hold (via the perturbation function).

For any $x\in X,$ the inequality $f^{**}(x)\leq f(x)$ follows from the Fenchel–Young inequality. For proper functions, $f=f^{**}$ if and only if $f$ is convex and lower semi-continuous by Fenchel–Moreau theorem.[3][4]

Convex minimization

A convex minimization (primal) problem is one of the form

find

\inf _{x\in M}f(x)

when given a convex function

f:X\to [-\infty ,\infty ]

and a convex subset

M\subseteq X.

Dual problem

In optimization theory, the duality principle states that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem.

In general given two dual pairs separated locally convex spaces $\left(X,X^{*}\right)$ and $\left(Y,Y^{*}\right).$ Then given the function $f:X\to [-\infty ,\infty ],$ we can define the primal problem as finding $x$ such that

\inf _{x\in X}f(x).

If there are constraint conditions, these can be built into the function $f$ by letting $f=f+I_{\mathrm {constraints} }$ where $I$ is the indicator function. Then let $F:X\times Y\to [-\infty ,\infty ]$ be a perturbation function such that $F(x,0)=f(x).$ [5]

The dual problem with respect to the chosen perturbation function is given by

\sup _{y^{*}\in Y^{*}}-F^{*}\left(0,y^{*}\right)

where $F^{*}$ is the convex conjugate in both variables of $F.$

The duality gap is the difference of the right and left hand sides of the inequality[6][5][7]

\sup _{y^{*}\in Y^{*}}-F^{*}\left(0,y^{*}\right)\leq \inf _{x\in X}F(x,0).

This principle is the same as weak duality. If the two sides are equal to each other, then the problem is said to satisfy strong duality.

There are many conditions for strong duality to hold such as:

$F=F^{**}$ where $F$ is the perturbation function relating the primal and dual problems and $F^{**}$ is the biconjugate of $F$ ;
the primal problem is a linear optimization problem;
Slater's condition for a convex optimization problem.[8][9]

Lagrange duality

For a convex minimization problem with inequality constraints,

\min {}_{x}f(x)

subject to

g_{i}(x)\leq 0

for

i=1,\ldots ,m.

the Lagrangian dual problem is

\sup {}_{u}\inf {}_{x}L(x,u)

subject to

u_{i}(x)\geq 0

for

i=1,\ldots ,m.

where the objective function $L(x,u)$ is the Lagrange dual function defined as follows:

L(x,u)=f(x)+\sum _{j=1}^{m}u_{j}g_{j}(x)

Notes

Rockafellar, R. Tyrrell (1997) [1970]. Convex Analysis. Princeton, NJ: Princeton University Press. ISBN 978-0-691-01586-6.
Rockafellar & Wets 2009, pp. 1–28.
Zălinescu 2002, pp. 75–79.
Borwein, Jonathan; Lewis, Adrian (2006). Convex Analysis and Nonlinear Optimization: Theory and Examples (2 ed.). Springer. pp. 76–77. ISBN 978-0-387-29570-1.
Boţ, Radu Ioan; Wanka, Gert; Grad, Sorin-Mihai (2009). Duality in Vector Optimization. Springer. ISBN 978-3-642-02885-4.
Zălinescu 2002, pp. 106–113.
Csetnek, Ernö Robert (2010). Overcoming the failure of the classical generalized interior-point regularity conditions in convex optimization. Applications of the duality theory to enlargements of maximal monotone operators. Logos Verlag Berlin GmbH. ISBN 978-3-8325-2503-3.
Borwein, Jonathan; Lewis, Adrian (2006). Convex Analysis and Nonlinear Optimization: Theory and Examples (2 ed.). Springer. ISBN 978-0-387-29570-1.
Boyd, Stephen; Vandenberghe, Lieven (2004). Convex Optimization (PDF). Cambridge University Press. ISBN 978-0-521-83378-3. Retrieved October 3, 2011.

The conclusion is immediate if $X=\{0\}$ so assume otherwise. Fix $x\in X.$ Replacing $f$ with the norm gives $\partial f(x)=\left\{x^{*}\in X^{*}~:~\left\langle x^{*},x\right\rangle -\|x\|\geq \left\langle x^{*},z\right\rangle -\|z\|{\text{ for all }}z\in X\right\}.$ If $x^{*}\in \partial f(x)$ and $r\geq 0$ is real then using $z:=rx$ gives $\left\langle x^{*},x\right\rangle -\|x\|\geq \left\langle x^{*},rx\right\rangle -\|rx\|=r\left[\left\langle x^{*},x\right\rangle -\|x\|\right],$ where in particular, taking $r:=2$ gives $x^{*}(x)\geq \|x\|$ while taking $r:={\frac {1}{2}}$ gives $x^{*}(x)\leq \|x\|$ and thus $x^{*}(x)=\|x\|$ ; moreover, if in addition $x\neq 0$ then because $x^{*}\left({\frac {x}{\|x\|}}\right)=1,$ it follows from the definition of the dual norm that $\left\|x^{*}\right\|\geq 1.$ Because $\partial f(x)\subseteq \left\{x^{*}\in X^{*}~:~x^{*}(x)=\|x\|\right\},$ which is equivalent to $\partial f(x)=\partial f(x)\cap \left\{x^{*}\in X^{*}~:~x^{*}(x)=\|x\|\right\},$ it follows that $\partial f(x)=\left\{x^{*}\in X^{*}~:~x^{*}(x)=\|x\|{\text{ and }}\|z\|\geq \left\langle x^{*},z\right\rangle {\text{ for all }}z\in X\right\},$ which implies $\left\|x^{*}\right\|\leq 1$ for all $x^{*}\in \partial f(x).$ From these facts, the conclusion can now be reached. ∎

References

Bauschke, Heinz H.; Combettes, Patrick L. (28 February 2017). Convex Analysis and Monotone Operator Theory in Hilbert Spaces. CMS Books in Mathematics. Springer Science & Business Media. ISBN 978-3-319-48311-5. OCLC 1037059594.
Boyd, Stephen; Vandenberghe, Lieven (8 March 2004). Convex Optimization. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge, U.K. New York: Cambridge University Press. ISBN 978-0-521-83378-3. OCLC 53331084.
Hiriart-Urruty, J.-B.; Lemaréchal, C. (2001). Fundamentals of convex analysis. Berlin: Springer-Verlag. ISBN 978-3-540-42205-1.
Kusraev, A.G.; Kutateladze, Semen Samsonovich (1995). Subdifferentials: Theory and Applications. Dordrecht: Kluwer Academic Publishers. ISBN 978-94-011-0265-0.
Rockafellar, R. Tyrrell; Wets, Roger J.-B. (26 June 2009). Variational Analysis. Grundlehren der mathematischen Wissenschaften. Vol. 317. Berlin New York: Springer Science & Business Media. ISBN 9783642024313. OCLC 883392544.
Rudin, Walter (1991). Functional Analysis. International Series in Pure and Applied Mathematics. Vol. 8 (Second ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 978-0-07-054236-5. OCLC 21163277.
Singer, Ivan (1997). Abstract convex analysis. Canadian Mathematical Society series of monographs and advanced texts. New York: John Wiley & Sons, Inc. pp. xxii+491. ISBN 0-471-16015-6. MR 1461544.
Stoer, J.; Witzgall, C. (1970). Convexity and optimization in finite dimensions. Vol. 1. Berlin: Springer. ISBN 978-0-387-04835-2.
Zălinescu, Constantin (30 July 2002). Convex Analysis in General Vector Spaces. River Edge, N.J. London: World Scientific Publishing. ISBN 978-981-4488-15-0. MR 1921556. OCLC 285163112 – via Internet Archive.

External links

Media related to Convex analysis at Wikimedia Commons

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Rockafellar-1] Rockafellar, R. Tyrrell (1997) [1970]. Convex Analysis. Princeton, NJ: Princeton University Press. ISBN 978-0-691-01586-6.

[FOOTNOTERockafellarWets20091–28-2] Rockafellar & Wets 2009, pp. 1–28.

[FOOTNOTEZălinescu200275–79-3] Zălinescu 2002, pp. 75–79.

[BorweinLewis-5] Borwein, Jonathan; Lewis, Adrian (2006). Convex Analysis and Nonlinear Optimization: Theory and Examples (2 ed.). Springer. pp. 76–77. ISBN 978-0-387-29570-1.

[BWG-6] Boţ, Radu Ioan; Wanka, Gert; Grad, Sorin-Mihai (2009). Duality in Vector Optimization. Springer. ISBN 978-3-642-02885-4.

[FOOTNOTEZălinescu2002106–113-7] Zălinescu 2002, pp. 106–113.

[Csetnek_2010-8] Csetnek, Ernö Robert (2010). Overcoming the failure of the classical generalized interior-point regularity conditions in convex optimization. Applications of the duality theory to enlargements of maximal monotone operators. Logos Verlag Berlin GmbH. ISBN 978-3-8325-2503-3.

[borwein-9] Borwein, Jonathan; Lewis, Adrian (2006). Convex Analysis and Nonlinear Optimization: Theory and Examples (2 ed.). Springer. ISBN 978-0-387-29570-1.

[boyd-10] Boyd, Stephen; Vandenberghe, Lieven (2004). Convex Optimization (PDF). Cambridge University Press. ISBN 978-0-521-83378-3. Retrieved October 3, 2011.

[4] The conclusion is immediate if $X=\{0\}$ so assume otherwise. Fix $x\in X.$ Replacing $f$ with the norm gives $\partial f(x)=\left\{x^{*}\in X^{*}~:~\left\langle x^{*},x\right\rangle -\|x\|\geq \left\langle x^{*},z\right\rangle -\|z\|{\text{ for all }}z\in X\right\}.$ If $x^{*}\in \partial f(x)$ and $r\geq 0$ is real then using $z:=rx$ gives $\left\langle x^{*},x\right\rangle -\|x\|\geq \left\langle x^{*},rx\right\rangle -\|rx\|=r\left[\left\langle x^{*},x\right\rangle -\|x\|\right],$ where in particular, taking $r:=2$ gives $x^{*}(x)\geq \|x\|$ while taking $r:={\frac {1}{2}}$ gives $x^{*}(x)\leq \|x\|$ and thus $x^{*}(x)=\|x\|$ ; moreover, if in addition $x\neq 0$ then because $x^{*}\left({\frac {x}{\|x\|}}\right)=1,$ it follows from the definition of the dual norm that $\left\|x^{*}\right\|\geq 1.$ Because $\partial f(x)\subseteq \left\{x^{*}\in X^{*}~:~x^{*}(x)=\|x\|\right\},$ which is equivalent to $\partial f(x)=\partial f(x)\cap \left\{x^{*}\in X^{*}~:~x^{*}(x)=\|x\|\right\},$ it follows that $\partial f(x)=\left\{x^{*}\in X^{*}~:~x^{*}(x)=\|x\|{\text{ and }}\|z\|\geq \left\langle x^{*},z\right\rangle {\text{ for all }}z\in X\right\},$ which implies $\left\|x^{*}\right\|\leq 1$ for all $x^{*}\in \partial f(x).$ From these facts, the conclusion can now be reached. ∎

Convex analysis and variational analysis
Basic concepts	Convex combination Convex function Convex set
Topics (list)	Choquet theory Convex geometry Convex metric space Convex optimization Duality Lagrange multiplier Legendre transformation Locally convex topological vector space Simplex
Maps	Convex conjugate Concave (Closed K- Logarithmically Proper Pseudo- Quasi-) Convex function Invex function Legendre transformation Semi-continuity Subderivative
Main results (list)	Carathéodory's theorem Ekeland's variational principle Fenchel–Moreau theorem Fenchel-Young inequality Jensen's inequality Hermite–Hadamard inequality Krein–Milman theorem Mazur's lemma Shapley–Folkman lemma Robinson-Ursescu Simons Ursescu
Sets	Convex hull (Orthogonally, Pseudo-) Convex set Effective domain Epigraph Hypograph John ellipsoid Lens Radial set/Algebraic interior Zonotope
Series	Convex series related ((cs, lcs)-closed, (cs, bcs)-complete, (lower) ideally convex, (Hx), and (Hwx))
Duality	Dual system Duality gap Strong duality Weak duality
Applications and related	Convexity in economics