Solution concept
In game theory, a solution concept is a formal rule for predicting how a game will be played. These predictions are called "solutions", and describe which strategies will be adopted by players and, therefore, the result of the game. The most commonly used solution concepts are equilibrium concepts, most famously Nash equilibrium.
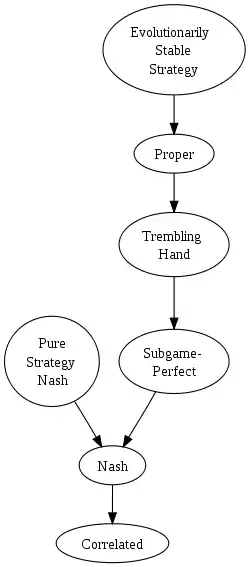
Many solution concepts, for many games, will result in more than one solution. This puts any one of the solutions in doubt, so a game theorist may apply a refinement to narrow down the solutions. Each successive solution concept presented in the following improves on its predecessor by eliminating implausible equilibria in richer games.
Formal definition
Let be the class of all games and, for each game , let be the set of strategy profiles of . A solution concept is an element of the direct product i.e., a function such that for all
Rationalizability and iterated dominance
In this solution concept, players are assumed to be rational and so strictly dominated strategies are eliminated from the set of strategies that might feasibly be played. A strategy is strictly dominated when there is some other strategy available to the player that always has a higher payoff, regardless of the strategies that the other players choose. (Strictly dominated strategies are also important in minimax game-tree search.) For example, in the (single period) prisoners' dilemma (shown below), cooperate is strictly dominated by defect for both players because either player is always better off playing defect, regardless of what his opponent does.
| Prisoner 2 Cooperate | Prisoner 2 Defect | |
|---|---|---|
| Prisoner 1 Cooperate | −0.5, −0.5 | −10, 0 |
| Prisoner 1 Defect | 0, −10 | −2, −2 |
Nash equilibrium
A Nash equilibrium is a strategy profile (a strategy profile specifies a strategy for every player, e.g. in the above prisoners' dilemma game (cooperate, defect) specifies that prisoner 1 plays cooperate and prisoner 2 plays defect) in which every strategy is a best response to every other strategy played. A strategy by a player is a best response to another player's strategy if there is no other strategy that could be played that would yield a higher pay-off in any situation in which the other player's strategy is played.
Backward induction
In some games, there are multiple Nash equilibria, but not all of them are realistic. In dynamic games, backward induction can be used to eliminate unrealistic Nash equilibria. Backward induction assumes that players are rational and will make the best decisions based on their future expectations. This eliminates noncredible threats, which are threats that a player would not carry out if they were ever called upon to do so.
For example, consider a dynamic game with an incumbent firm and a potential entrant to the industry. The incumbent has a monopoly and wants to maintain its market share. If the entrant enters, the incumbent can either fight or accommodate the entrant. If the incumbent accommodates, the entrant will enter and gain profit. If the incumbent fights, it will lower its prices, run the entrant out of business (incurring exit costs), and damage its own profits.
The best response for the incumbent if the entrant enters is to accommodate, and the best response for the entrant if the incumbent accommodates is to enter. This results in a Nash equilibrium. However, if the incumbent chooses to fight, the best response for the entrant is to not enter. If the entrant does not enter, it does not matter what the incumbent chooses to do. Hence, fight can be considered a best response for the incumbent if the entrant does not enter, resulting in another Nash equilibrium.
However, this second Nash equilibrium can be eliminated by backward induction because it relies on a noncredible threat from the incumbent. By the time the incumbent reaches the decision node where it can choose to fight, it would be irrational to do so because the entrant has already entered. Therefore, backward induction eliminates this unrealistic Nash equilibrium.
See also:
Subgame perfect Nash equilibrium
A generalization of backward induction is subgame perfection. Backward induction assumes that all future play will be rational. In subgame perfect equilibria, play in every subgame is rational (specifically a Nash equilibrium). Backward induction can only be used in terminating (finite) games of definite length and cannot be applied to games with imperfect information. In these cases, subgame perfection can be used. The eliminated Nash equilibrium described above is subgame imperfect because it is not a Nash equilibrium of the subgame that starts at the node reached once the entrant has entered.
Perfect Bayesian equilibrium
Sometimes subgame perfection does not impose a large enough restriction on unreasonable outcomes. For example, since subgames cannot cut through information sets, a game of imperfect information may have only one subgame – itself – and hence subgame perfection cannot be used to eliminate any Nash equilibria. A perfect Bayesian equilibrium (PBE) is a specification of players’ strategies and beliefs about which node in the information set has been reached by the play of the game. A belief about a decision node is the probability that a particular player thinks that node is or will be in play (on the equilibrium path). In particular, the intuition of PBE is that it specifies player strategies that are rational given the player beliefs it specifies and the beliefs it specifies are consistent with the strategies it specifies.
In a Bayesian game a strategy determines what a player plays at every information set controlled by that player. The requirement that beliefs are consistent with strategies is something not specified by subgame perfection. Hence, PBE is a consistency condition on players’ beliefs. Just as in a Nash equilibrium no player's strategy is strictly dominated, in a PBE, for any information set no player's strategy is strictly dominated beginning at that information set. That is, for every belief that the player could hold at that information set there is no strategy that yields a greater expected payoff for that player. Unlike the above solution concepts, no player's strategy is strictly dominated beginning at any information set even if it is off the equilibrium path. Thus in PBE, players cannot threaten to play strategies that are strictly dominated beginning at any information set off the equilibrium path.
The Bayesian in the name of this solution concept alludes to the fact that players update their beliefs according to Bayes' theorem. They calculate probabilities given what has already taken place in the game.
Forward induction
Forward induction is so called because just as backward induction assumes future play will be rational, forward induction assumes past play was rational. Where a player does not know what type another player is (i.e. there is imperfect and asymmetric information), that player may form a belief of what type that player is by observing that player's past actions. Hence the belief formed by that player of what the probability of the opponent being a certain type is based on the past play of that opponent being rational. A player may elect to signal his type through his actions.
Kohlberg and Mertens (1986) introduced the solution concept of Stable equilibrium, a refinement that satisfies forward induction. A counter-example was found where such a stable equilibrium did not satisfy backward induction. To resolve the problem Jean-François Mertens introduced what game theorists now call Mertens-stable equilibrium concept, probably the first solution concept satisfying both forward and backward induction.
Forward induction yields a unique solution for the burning money game.
See also
References
- Cho, I-K.; Kreps, D. M. (1987). "Signaling Games and Stable Equilibria". Quarterly Journal of Economics. 102 (2): 179–221. CiteSeerX 10.1.1.407.5013. doi:10.2307/1885060. JSTOR 1885060. S2CID 154404556.
- Fudenberg, Drew; Tirole, Jean (1991). Game theory. Cambridge, Massachusetts: MIT Press. ISBN 9780262061414. Book preview.
- Harsanyi, J. (1973) Oddness of the number of equilibrium points: a new proof. International Journal of Game Theory 2:235–250.
- Govindan, Srihari & Robert Wilson, 2008. "Refinements of Nash Equilibrium," The New Palgrave Dictionary of Economics, 2nd Edition.
- Hines, W. G. S. (1987) Evolutionary stable strategies: a review of basic theory. Theoretical Population Biology 31:195–272.
- Kohlberg, Elon & Jean-François Mertens, 1986. "On the Strategic Stability of Equilibria," Econometrica, Econometric Society, vol. 54(5), pages 1003-37, September.
- Leyton-Brown, Kevin; Shoham, Yoav (2008). Essentials of Game Theory: A Concise, Multidisciplinary Introduction. San Rafael, CA: Morgan & Claypool Publishers. ISBN 978-1-59829-593-1.
- Mertens, Jean-François, 1989. "Stable Equilibria - A reformulation. Part 1 Basic Definitions and Properties," Mathematics of Operations Research, Vol. 14, No. 4, Nov.
- Noldeke, G. & Samuelson, L. (1993) An evolutionary analysis of backward and forward induction. Games & Economic Behaviour 5:425–454.
- Maynard Smith, J. (1982) Evolution and the Theory of Games. ISBN 0-521-28884-3
- Osborne, Martin J.; Rubinstein, Ariel (1994). A course in game theory. MIT Press. ISBN 978-0-262-65040-3..
- Selten, R. (1983) Evolutionary stability in extensive two-person games. Math. Soc. Sci. 5:269–363.
- Selten, R. (1988) Evolutionary stability in extensive two-person games – correction and further development. Math. Soc. Sci. 16:223–266
- Shoham, Yoav; Leyton-Brown, Kevin (2009). Multiagent Systems: Algorithmic, Game-Theoretic, and Logical Foundations. New York: Cambridge University Press. ISBN 978-0-521-89943-7.
- Thomas, B. (1985a) On evolutionary stable sets. J. Math. Biol. 22:105–115.
- Thomas, B. (1985b) Evolutionary stable sets in mixed-strategist models. Theor. Pop. Biol. 28:332–341