Feuerbach hyperbola
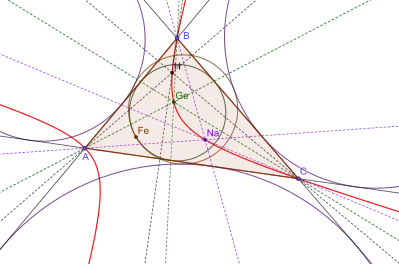
In geometry, the Feuerbach hyperbola is a rectangular hyperbola passing through important triangle centers such as the Orthocenter, Gergonne point, Nagel point and Shiffler point. The center of the hyperbola is the Feuerbach point, the point of tangency of the incircle and the nine-point circle.[1]
Equation
It has the trilinear equation (here are the angles at the respective vertices and is the barycentric coordinate).[2]
Properties
Like other rectangular hyperbolas, the orthocenter of any three points on the curve lies on the hyperbola. So, the orthocenter of the triangle lies on the curve.
The line is tangent to this hyperbola at .
Isogonal conjugate of OI
The hyperbola is the isogonal conjugate of , the line joining the circumcenter and the incenter.[3] This fact leads to a few interesting properties. Specifically all the points lying on the line have their isogonal conjugates lying on the hyperbola. The Nagel point lies on the curve since its isogonal conjugate is the point of concurrency of the lines joining the vertices and the opposite Mixtilinear incircle touchpoints, also the in-similitude of the incircle and the circumcircle. Similarly, the Gergonne point lies on the curve since its isogonal conjugate is the ex-similitude of the incircle and the circumcircle.
The pedal circle of any point on the hyperbola passes through the Feuerbach point, the center of the hyperbola.
Kariya's theorem
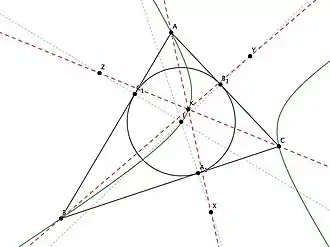
Given a triangle , let be the touchpoints of the incircle with the sides of the triangle opposite to vertices respectively. Let be points lying on the lines such that . Then, the lines are concurrent at a point lying on the Feuerbach hyperbola.
The Kariya's theorem has a long history.[4] It was proved independently by Auguste Boutin and V. Retali.,[5][6][7] but it became famous only after Kariya's paper.[8] Around that time, many generalizations of this result were given. Kariya's theorem can be used for the construction of the Feuerbach hyperbola.
Both Lemoine's theorem and Kariya's theorem are a special case of Jacobi's theorem.
See also
Other rectangular hyperbolas
- Kiepert hyperbola, the unique conic which passes through a triangle's three vertices, its centroid, and its orthocenter
- Jeřábek hyperbola, a rectangular hyperbola centered on a triangle's nine-point circle and passing through the triangle's three vertices as well as its circumcenter, orthocenter, and various other notable centers
References
- Boucher, H. (1893). "Essai de classification sur les races gallines". Annales de la Société linnéenne de Lyon. 40 (1): 89–100. doi:10.3406/linly.1893.4047. ISSN 1160-6398.
- Parry, C. F. (2001). "Triangle centers and central triangles, by Clark Kimberling (Congress Numerantium Vol. 129) Pp. 295. $42.50 1998. ISSN 0316-1282 (Utilitas Mathematica Publishing, Inc., Winnipeg)". The Mathematical Gazette. 85 (502): 172–173. doi:10.2307/3620531. ISSN 0025-5572. JSTOR 3620531. S2CID 227212286.
- Rigby, J. F. (1973). "A concentrated dose of old-fashioned geometry". The Mathematical Gazette. 57 (402): 296–298. doi:10.2307/3616051. ISSN 0025-5572. JSTOR 3616051. S2CID 126241645.
- "Problems and Solutions". The American Mathematical Monthly. 119 (8): 699. 2012. doi:10.4169/amer.math.monthly.119.08.699. S2CID 37903933.
- Kahane, J. (1961). "Problèmes et remarques sur les carrés de convolution". Colloquium Mathematicum. 8 (2): 263–265. doi:10.4064/cm-8-2-263-265. ISSN 0010-1354.
- Humbert, G. (1890). "Sur les coniques inscrites à une quartique". Annales de la faculté des sciences de Toulouse Mathématiques. 4 (3): 1–8. doi:10.5802/afst.55. ISSN 0996-0481.
- "Periodico di Matematica per ľinsegnamento secondario". Rendiconti del Circolo Matematico di Palermo. 3 (2): 56. 1889. doi:10.1007/bf03017173. ISSN 0009-725X. S2CID 184480136.
- Kariya, J. (1904). "Un probleme sur le triangle,"L'Enseignement mathematiques": 130–132, 236, 406.
{{cite journal}}: Cite journal requires|journal=(help)