Xcas
Xcas is a user interface to Giac, which is an open source[2] computer algebra system (CAS) for Windows, macOS and Linux among many other platforms. Xcas is written in C++.[3] Giac can be used directly inside software written in C++.
Xcas, the swiss knife for mathematics | |
 | |
| Developer(s) | Bernard Parisse |
|---|---|
| Initial release | 2000 |
| Stable release | |
| Repository | |
| Written in | C++ |
| Operating system | Windows, macOS, Linux, FreeBSD, Android, iOS |
| Type | Computer algebra system (CAS) |
| License | GNU GPL |
| Website | xcas |
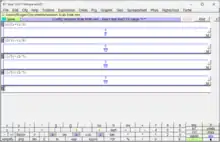


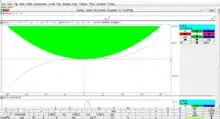
Xcas has compatibility modes with many popular algebra systems like WolframAlpha,[4] Mathematica,[5] Maple,[6] or MuPAD. Users can use Giac/Xcas to develop formal algorithms or use it in other software. Giac is used in SageMath[4] for calculus operations. Among other things, Xcas can solve equations (Figure 3) and differential equations (Figure 4) and draw graphs. There is a forum for questions about Xcas.[7]
CmathOOoCAS, an OpenOffice.org plugin which allows formal calculation in Calc spreadsheet and Writer word processing, uses Giac to perform calculations.[8]
Features
Here is a brief overview of what Xcas is able to do:[9][10]
- Xcas has the ability of a scientific calculator that provides show input and writes pretty print
- Xcas works also as a spreadsheet;[11]
- computer algebra;
- 2D geometry in the plane;[12]
- 3D geometry in space;[12]
- spreadsheet;[11]
- statistics;
- regression (exponential, linear, logarithmic, logistic, polynomial, power)
- programming;[13]
- solve equations even with complex roots (Figure 2);
- solving trigonometric equations
- solve differential equations[14][15] (Figure 3);
- draw graphs;
- calculate differential (or derivative) of functions (Figure 2);
- calculate antiderivative of functions (Figure 2);
- calculate area and integral calculus;
- linear algebra[16]
Example Xcas commands:
- Produce mixed fractions:
propfrac(42/15)gives 2 + 4/5 - Calculate square root:
sqrt(4)= 2 - Draw a vertical line in coordinate system:
line(x=1)draws the vertical line in the output window - Draw graph:
plot(function)(for example,plot(3 * x^2 - 5)produces a plot of y = 3x2 − 5 - Calculate average:
mean([3, 4, 2])is 3 - Calculate variance:
variance([3, 4, 2])is 2/3 - Calculate standard deviation:
stddev([3, 4, 2])is √6/3 - Calculate determinant of a matrix: {{code|det([[1,2], [3,4]])}} is −2
- Calculate local extrema of a function:
extrema(-2*cos(x)-cos(x)^2,x)is [0, π] - Calculate cross product of two vectors:
cross([1, 2, 3], [4, 3, 2])is [-5, 10, -5] - Calculate permutations:
nPr() - Calculate combinations:
nCr() - Solve equation:
solve(equation,x) - Factoring Polynomials:
factor(polynomial,x)orcfactor(polynomial,x) - Differentiation of function:
diff(function,x) - Calculate indefinite integrals/antiderivatives:
int(function,x) - Calculate definite integrals/area under the curve of a function:
int(function,x,lowerlimit,upperlimit)- Calculate definite integral aka solid of revolution - finding volume by rotation (around the x-axis):
int(pi*function^2,x,lowerlimit,upperlimit) - Calculate definite integral aka solid of revolution - finding volume by rotation (around the y-axis) for a decreasing function:
int(2*pi*x*function,x,lowerlimit,upperlimit)
- Calculate definite integral aka solid of revolution - finding volume by rotation (around the x-axis):
- Separation of variables:
split((x+1)*(y-2),[x,y])produces - desolve differential equation (the derivatives are written as y′ or y″):
desolve(differential equation,y)
Supported operating systems
History
Xcas and Giac are open-source projects developed and written by Bernard Parisse and Renée De Graeve at the former Joseph Fourier University of Grenoble (now the Grenoble Alpes University),[24] France since 2000.[25] Xcas and Giac are based on experiences gained with Parisse's former project Erable.[26] Pocket CAS and CAS Calc P11 utilize Giac.
The system was also chosen by Hewlett-Packard as the CAS for their HP Prime calculator, which utilizes the Giac/Xcas 1.5.0 engine under a dual-license scheme.
In 2013, the mathematical software Xcas was also integrated into GeoGebra's CAS view.[27]
Use in education
Since 2015, Xcas is used in the French education system.[28][29][30][31] Xcas is also[32] used in German[33] universities,[34][35] and in Spain and Mexico.[36] It is also used at the University of North Carolina Wilmington[37] and the University of New Mexico.[38] Xcas[39] is used in particular for learning algebra.[40]
χCAS
There is a port of Giac/Xcas for Casio graphing calculators: fx-CG10, fx-CG20, fx-CG50, fx-9750GIII, fx-9860GIII, called χCAS (KhiCAS). These calculators do not have their own computer algebra system. It is also available for TI Nspire CX, CX-II, and Numworks N0110[41]
References
- "Index of /~parisse/debian/dists/stable/main/source".
- "Giac/Xcas and Pari/GP" (PDF).
- "Elsevier Enhanced Reader". reader.elsevier.com. Retrieved 2022-06-08.
- Tõnisson, Eno (2017-11-09). Differences between expected answers and the answers offered by computer algebra systems to school mathematics equations (Thesis). hdl:10062/58398.
- "Computer Algebra in Education". math.unm.edu. Retrieved 2022-01-03.
- "xcas - Computer Algebra System - console and graphical calculator". reposcope.com. Retrieved 2020-04-12.
- "Le forum de XCAS - Page d'accueil". xcas.univ-grenoble-alpes.fr. Retrieved 2020-04-12.
- "An introduction to the Xcas interface" (PDF).
- "MATHEMATICS EDUCATION AS A SCIENCE AND A PROFESSION" (PDF). Josip Juraj Strossmayer University of Osijek. 2019-05-02. Retrieved 2017-10-05.
- Read more commands and features hear.
- "Xcas reference card".
- Gandit, Michèle (2009). Bardini, C.; Fortin, P.; Oldknow, A.; Vagost, D. (eds.). Experimenting and proof in mathematics with XCAS. Proceedings of the 9th International Conference on Technology in Mathematics Teaching. Metz, France. CiteSeerX 10.1.1.580.4878.
- Halkos, George E.; Tsilika, Kyriaki D. (2015). "Using Xcas in Calculus Curricula: a Plan of Lectures and Laboratory Projects". Computational and Applied Mathematics Journal. 1 (3). S2CID 58451849.
- Halkos, George E.; Tsilika, Kyriaki D.; Simos, Theodore E.; Psihoyios, George; Tsitouras, Ch.; Anastassi, Zacharias (2011). "Xcas as a Programming Environment for Stability Conditions for a Class of Differential Equation Models in Economics". Numerical Analysis and Applied Mathematics Icnaam 2011: International Conference on Numerical Analysis and Applied Mathematics. AIP Conference Proceedings. 1389 (1): 1769–1772. Bibcode:2011AIPC.1389.1769H. doi:10.1063/1.3636951.
- Fleurant, Cyril; Bodin-Fleurant, Sandrine (2019). "Integration and Differential Equations". Mathematics for Earth Science and Geography. Springer Textbooks in Earth Sciences, Geography and Environment. pp. 145–177. doi:10.1007/978-3-319-69242-5_6. ISBN 978-3-319-69241-8. S2CID 189288194.
- "Computeralgebra-Rundbrief Nr. 62: Fachgruppe Computeralgebra" (PDF). Gesellschaft für Informatik e.V. 2019-05-02. Retrieved 2018-03-02. (in German)
- "Xcas for Windows". logitheque. 2016-06-09. Retrieved 2018-12-05.
- "Installing Xcas". www-fourier.ujf-grenoble.fr. Retrieved 2021-11-14.
- "Symbolic Algebra Everywhere". Joey Bernard. 2015-12-15. Retrieved 2018-12-05.
- "Xcas Calcul Formel Lycee | PDF | Intégral | Variable (Mathématiques)".
- "Giac/Xcas, a free computer algebra system". www-fourier.ujf-grenoble.fr. Retrieved 2022-02-10.
- "Xcas Pad – Apps i Google Play". play.google.com (in Danish). Retrieved 2021-11-14.
- "Xcas en ligne". www.xcasenligne.fr. Retrieved 2022-03-18.
- "Planète MATHS - Liste des ressources par niveau". www.ac-grenoble.fr. Retrieved 2022-01-03.
- Fekih, Lassaad Ben; Verlinden, Olivier; Kouroussis, Georges (2011). Development of a user-friendly and open-source multibody framework with the help of symbolic tools. 4th International Congress Design and Modelling of Mechanical Systems. Sousse (Tunisia).
- MacCallum, Malcolm A. H. (December 2018). "Computer algebra in gravity research". Living Reviews in Relativity. 21 (1): 6. Bibcode:2018LRR....21....6M. doi:10.1007/s41114-018-0015-6. PMC 6105178. PMID 30174551.
- "Xcas | Semantic Scholar". www.semanticscholar.org. Retrieved 2022-02-10.
- "Liens mathématiques - Lycée Rosa Parks de Montgeron". www.lyc-rosaparks-montgeron.ac-versailles.fr. Retrieved 2022-01-03.
- "M@ths en LIgne". membres-ljk.imag.fr. Retrieved 2022-01-03.
- "Articles en ligne". www.epi.asso.fr. Retrieved 2022-01-03.
- "Quelles compétences mathématiques sont sollicitées en physique-chimie et SVT au lycée, et nécessaires pour la licence ?" (PDF).
- "Module 2 - Introduction". www.didaktik.mathematik.uni-wuerzburg.de. Retrieved 2022-01-03.
- Halkos, George; Tsilika, Kyriaki (November 2014). "Perspectives on integrating a computer algebra system into advanced calculus curricula". mpra.ub.uni-muenchen.de. Retrieved 2022-01-03.
- "Computeralgebra. Rundbrief" (PDF).
- "Abschlussbericht "Intelligentes Lernen"" (PDF).
- Salat Figols, Ramón Sebastián (2013). "La enseñanza de las matemáticas y la tecnología" [The teaching of mathematics and technology]. Revista Innovación Educativa (in Spanish). 13 (62): 61–74.
- "Xcas_session". people.uncw.edu. Retrieved 2022-01-03.
- "Computer Algebra in Education". math.unm.edu. Retrieved 2022-01-03.
- "Top PDF computer algebra - 1Library". 1library.net. Retrieved 2022-01-03.
- "THE DERIVE - NEWSLETTER #99" (PDF).
- https://www-fourier.ujf-grenoble.fr/~parisse/install_en
Further reading
- De Graeve, Renée (2018-01-19) [2013]. "Symbolic computation and Mathematics with the calculator HP Prime" (PDF). Translated by Lecointre, Jean Michel. Retrieved 2018-01-22.
- Parisse, Bernard (2007): "Symbolic algebra and Mathematics with Xcas" (list of commands) (PDF). Retrieved 2022-06-08.
- Parisse, B., University of Grenoble (January, 2016) "Giac/Xcas and Pari/GP" (PDF). Retrieved 2022-06-08.
- Halkos, George (2015-04-25) [2014]. "Perspectives on integrating a computer algebra system into advanced calculus curricula" (PDF). Retrieved 2019-09-06.
- Verlinden, Olivier (2013): "Symbolic generation of the kinematics of multibody systems in EasyDyn: From MuPAD to Xcas/Giac.". Retrieved 2022-06-08.
- http://www.mathsaulycee.sitew.com/fs/premiere_s/8uoow-xcas_commande_utile.pdf (French)
- http://briand-lyc.spip.ac-rouen.fr/IMG/pdf/xcas_fonctions.pdf (French)
- Barnard Parisse: Mathématiques avec Xcas. (French)
- Les Maths et Mes Tics (French)
- Fabian Reimers (editor): "Computeralgebra-Rundbrief Nr. 62: Fachgruppe Computeralgebra" (PDF). (German)