SymPy
SymPy is an open-source Python library for symbolic computation. It provides computer algebra capabilities either as a standalone application, as a library to other applications, or live on the web as SymPy Live[2] or SymPy Gamma.[3] SymPy is simple to install and to inspect because it is written entirely in Python with few dependencies.[4][5][6] This ease of access combined with a simple and extensible code base in a well known language make SymPy a computer algebra system with a relatively low barrier to entry.
 | |
| Developer(s) | SymPy Development Team |
|---|---|
| Initial release | 2007 |
| Stable release | 1.12[1]
/ 10 May 2023 |
| Repository | |
| Written in | Python |
| Operating system | Cross-platform |
| Type | Computer algebra system |
| License | New BSD License |
| Website | www |
SymPy includes features ranging from basic symbolic arithmetic to calculus, algebra, discrete mathematics, and quantum physics. It is capable of formatting the result of the computations as LaTeX code.[4][5]
SymPy is free software and is licensed under the New BSD license. The lead developers are Ondřej Čertík and Aaron Meurer. It was started in 2005 by Ondřej Čertík.[7]
Features
The SymPy library is split into a core with many optional modules.
Currently, the core of SymPy has around 260,000 lines of code[8] (it also includes a comprehensive set of self-tests: over 100,000 lines in 350 files as of version 0.7.5), and its capabilities include:[4][5][9][10][11]
Core capabilities
- Basic arithmetic: *, /, +, -, **
- Simplification
- Expansion
- Functions: trigonometric, hyperbolic, exponential, roots, logarithms, absolute value, spherical harmonics, factorials and gamma functions, zeta functions, polynomials, hypergeometric, special functions, etc.
- Substitution
- Arbitrary precision integers, rationals and floats
- Noncommutative symbols
- Pattern matching
Polynomials
- Basic arithmetic: division, gcd, etc.
- Factorization
- Square-free factorization
- Gröbner bases
- Partial fraction decomposition
- Resultants
Calculus
- Limits
- Differentiation
- Integration: Implemented Risch–Norman heuristic
- Taylor series (Laurent series)
Solving equations
Discrete math
- Binomial coefficients
- Summations
- Products
- Number theory: generating Prime numbers, primality testing, integer factorization, etc.
- Logic expressions[12]
Matrices
- Basic arithmetic
- Eigenvalues and their eigenvectors when the characteristic polynomial is solvable by radicals
- Determinants
- Inversion
- Solving
Geometry
- Points, lines, rays, ellipses, circles, polygons, etc.
- Intersections
- Tangency
- Similarity
Plotting
Note, plotting requires the external Matplotlib or Pyglet module.
- Coordinate models
- Plotting Geometric Entities
- 2D and 3D
- Interactive interface
- Colors
- Animations
Physics
Statistics
Combinatorics
- Permutations
- Combinations
- Partitions
- Subsets
- Permutation group: Polyhedral, Rubik, Symmetric, etc.
- Prufer sequence and Gray codes
Printing
- Pretty-printing: ASCII/Unicode pretty-printing, LaTeX
- Code generation: C, Fortran, Python
Related projects
- SageMath: an open source alternative to Mathematica, Maple, MATLAB, and Magma (SymPy is included in Sage)
- SymEngine: a rewriting of SymPy's core in C++, in order to increase its performance. Work is currently in progress to make SymEngine the underlying engine of Sage too.[14]
- mpmath: a Python library for arbitrary-precision floating-point arithmetic[15]
- SympyCore: another Python computer algebra system[16]
- SfePy: Software for solving systems of coupled partial differential equations (PDEs) by the finite element method in 1D, 2D and 3D.[17]
- GAlgebra: Geometric algebra module (previously sympy.galgebra).[18]
- Quameon: Quantum Monte Carlo in Python.[19]
- Lcapy: Experimental Python package for teaching linear circuit analysis.[20]
- LaTeX Expression project: Easy LaTeX typesetting of algebraic expressions in symbolic form with automatic substitution and result computation.[21]
- Symbolic statistical modeling: Adding statistical operations to complex physical models.[22]
- Diofant: a fork of SymPy, started by Sergey B Kirpichev[23]
Dependencies
Since version 1.0, SymPy has the mpmath package as a dependency.
There are several optional dependencies that can enhance its capabilities:
- gmpy: If gmpy is installed, SymPy's polynomial module will automatically use it for faster ground types. This can provide a several times boost in performance of certain operations.
- matplotlib: If matplotlib is installed, SymPy can use it for plotting.
- Pyglet: Alternative plotting package.
Usage examples
Pretty-printing
Sympy allows outputs to be formatted into a more appealing format through the pprint function. Alternatively, the init_printing() method will enable pretty-printing, so pprint need not be called. Pretty-printing will use unicode symbols when available in the current environment, otherwise it will fall back to ASCII characters.
>>> from sympy import pprint, init_printing, Symbol, sin, cos, exp, sqrt, series, Integral, Function
>>>
>>> x = Symbol("x")
>>> y = Symbol("y")
>>> f = Function("f")
>>> # pprint will default to unicode if available
>>> pprint(x ** exp(x))
⎛ x⎞
⎝ℯ ⎠
x
>>> # An output without unicode
>>> pprint(Integral(f(x), x), use_unicode=False)
/
|
| f(x) dx
|
/
>>> # Compare with same expression but this time unicode is enabled
>>> pprint(Integral(f(x), x), use_unicode=True)
⌠
⎮ f(x) dx
⌡
>>> # Alternatively, you can call init_printing() once and pretty-print without the pprint function.
>>> init_printing()
>>> sqrt(sqrt(exp(x)))
____
4 ╱ x
╲╱ ℯ
>>> (1/cos(x)).series(x, 0, 10)
2 4 6 8
x 5⋅x 61⋅x 277⋅x ⎛ 10⎞
1 + ── + ──── + ───── + ────── + O⎝x ⎠
2 24 720 8064
Expansion
>>> from sympy import init_printing, Symbol, expand
>>> init_printing()
>>>
>>> a = Symbol("a")
>>> b = Symbol("b")
>>> e = (a + b) ** 3
>>> e
(a + b)³
>>> e.expand()
a³ + 3⋅a²⋅b + 3⋅a⋅b² + b³
Arbitrary-precision example
>>> from sympy import Rational, pprint
>>> e = 2**50 / Rational(10) ** 50
>>> pprint(e)
1/88817841970012523233890533447265625
Differentiation
>>> from sympy import init_printing, symbols, ln, diff
>>> init_printing()
>>> x, y = symbols("x y")
>>> f = x**2 / y + 2 * x - ln(y)
>>> diff(f, x)
2⋅x
─── + 2
y
>>> diff(f, y)
2
x 1
- ── - ─
2 y
y
>>> diff(diff(f, x), y)
-2⋅x
────
2
y
Plotting
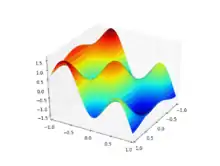
>>> from sympy import symbols, cos
>>> from sympy.plotting import plot3d
>>> x, y = symbols("x y")
>>> plot3d(cos(x * 3) * cos(y * 5) - y, (x, -1, 1), (y, -1, 1))
<sympy.plotting.plot.Plot object at 0x3b6d0d0>
Limits
>>> from sympy import init_printing, Symbol, limit, sqrt, oo
>>> init_printing()
>>>
>>> x = Symbol("x")
>>> limit(sqrt(x**2 - 5 * x + 6) - x, x, oo)
-5/2
>>> limit(x * (sqrt(x**2 + 1) - x), x, oo)
1/2
>>> limit(1 / x**2, x, 0)
∞
>>> limit(((x - 1) / (x + 1)) ** x, x, oo)
-2
ℯ
Differential equations
>>> from sympy import init_printing, Symbol, Function, Eq, dsolve, sin, diff
>>> init_printing()
>>>
>>> x = Symbol("x")
>>> f = Function("f")
>>>
>>> eq = Eq(f(x).diff(x), f(x))
>>> eq
d
──(f(x)) = f(x)
dx
>>>
>>> dsolve(eq, f(x))
x
f(x) = C₁⋅ℯ
>>>
>>> eq = Eq(x**2 * f(x).diff(x), -3 * x * f(x) + sin(x) / x)
>>> eq
2 d sin(x)
x ⋅──(f(x)) = -3⋅x⋅f(x) + ──────
dx x
>>>
>>> dsolve(eq, f(x))
C₁ - cos(x)
f(x) = ───────────
x³
Integration
>>> from sympy import init_printing, integrate, Symbol, exp, cos, erf
>>> init_printing()
>>> x = Symbol("x")
>>> # Polynomial Function
>>> f = x**2 + x + 1
>>> f
2
x + x + 1
>>> integrate(f, x)
3 2
x x
── + ── + x
3 2
>>> # Rational Function
>>> f = x / (x**2 + 2 * x + 1)
>>> f
x
────────────
2
x + 2⋅x + 1
>>> integrate(f, x)
1
log(x + 1) + ─────
x + 1
>>> # Exponential-polynomial functions
>>> f = x**2 * exp(x) * cos(x)
>>> f
2 x
x ⋅ℯ ⋅cos(x)
>>> integrate(f, x)
2 x 2 x x x
x ⋅ℯ ⋅sin(x) x ⋅ℯ ⋅cos(x) x ℯ ⋅sin(x) ℯ ⋅cos(x)
──────────── + ──────────── - x⋅ℯ ⋅sin(x) + ───────── - ─────────
2 2 2 2
>>> # A non-elementary integral
>>> f = exp(-(x**2)) * erf(x)
>>> f
2
-x
ℯ ⋅erf(x)
>>> integrate(f, x)
___ 2
╲╱ π ⋅erf (x)
─────────────
4
Series
>>> from sympy import Symbol, cos, sin, pprint
>>> x = Symbol("x")
>>> e = 1 / cos(x)
>>> pprint(e)
1
──────
cos(x)
>>> pprint(e.series(x, 0, 10))
2 4 6 8
x 5⋅x 61⋅x 277⋅x ⎛ 10⎞
1 + ── + ──── + ───── + ────── + O⎝x ⎠
2 24 720 8064
>>> e = 1/sin(x)
>>> pprint(e)
1
──────
sin(x)
>>> pprint(e.series(x, 0, 4))
3
1 x 7⋅x ⎛ 4⎞
─ + ─ + ──── + O⎝x ⎠
x 6 360
Example 1
>>> from sympy import *
>>> x = Symbol("x")
>>> y = Symbol("y")
>>> facts = Q.positive(x), Q.positive(y)
>>> with assuming(*facts):
... print(ask(Q.positive(2 * x + y)))
True
Example 2
>>> from sympy import *
>>> x = Symbol("x")
>>> # Assumption about x
>>> fact = [Q.prime(x)]
>>> with assuming(*fact):
... print(ask(Q.rational(1 / x)))
True
References
- "Releases - sympy/sympy". Retrieved 6 September 2022 – via GitHub.
- "SymPy Live". live.sympy.org. Retrieved 2021-08-25.
- "SymPy Gamma". www.sympygamma.com. Retrieved 2021-08-25.
- "SymPy homepage". Retrieved 2014-10-13.
- Joyner, David; Čertík, Ondřej; Meurer, Aaron; Granger, Brian E. (2012). "Open source computer algebra systems: SymPy". ACM Communications in Computer Algebra. 45 (3/4): 225–234. doi:10.1145/2110170.2110185. S2CID 44862851.
- Meurer, Aaron; Smith, Christopher P.; Paprocki, Mateusz; Čertík, Ondřej; Kirpichev, Sergey B.; Rocklin, Matthew; Kumar, AMiT; Ivanov, Sergiu; Moore, Jason K. (2017-01-02). "SymPy: symbolic computing in Python" (PDF). PeerJ Computer Science. 3: e103. doi:10.7717/peerj-cs.103. ISSN 2376-5992.
- "SymPy vs. Mathematica · sympy/Sympy Wiki". GitHub.
- "Sympy project statistics on Open HUB". Retrieved 2014-10-13.
- Gede, Gilbert; Peterson, Dale L.; Nanjangud, Angadh; Moore, Jason K.; Hubbard, Mont (2013). Constrained multibody dynamics with Python: From symbolic equation generation to publication. ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers. pp. V07BT10A051. doi:10.1115/DETC2013-13470. ISBN 978-0-7918-5597-3.
- Rocklin, Matthew; Terrel, Andy (2012). "Symbolic Statistics with SymPy". Computing in Science & Engineering. 14 (3): 88–93. Bibcode:2012CSE....14c..88R. doi:10.1109/MCSE.2012.56. S2CID 18307629.
- Asif, Mushtaq; Olaussen, Kåre (2014). "Automatic code generator for higher order integrators". Computer Physics Communications. 185 (5): 1461–1472. arXiv:1310.2111. Bibcode:2014CoPhC.185.1461M. doi:10.1016/j.cpc.2014.01.012. S2CID 42041635.
- "Assumptions Module — SymPy 1.4 documentation". docs.sympy.org. Retrieved 2019-07-05.
- "Continuum Mechanics — SymPy 1.4 documentation". docs.sympy.org. Retrieved 2019-07-05.
- "GitHub - symengine/symengine: SymEngine is a fast symbolic manipulation library, written in C++". GitHub. Retrieved 2021-08-25.
- "mpmath - Python library for arbitrary-precision floating-point arithmetic". mpmath.org. Retrieved 2021-08-25.
- "GitHub - pearu/sympycore: Automatically exported from code.google.com/p/sympycore". GitHub. January 2021. Retrieved 2021-08-25.
- Developers, SfePy. "SfePy: Simple Finite Elements in Python — SfePy version: 2021.2+git.13ca95f1 documentation". sfepy.org. Retrieved 2021-08-25.
- "GitHub - pygae/galgebra: Symbolic Geometric Algebra/Calculus package for SymPy". GitHub. Retrieved 2021-08-25.
- "Quameon - Quantum Monte Carlo in Python". quameon.sourceforge.net. Retrieved 2021-08-25.
- "Welcome to Lcapy's documentation! — Lcapy 0.76 documentation". 2021-01-16. Archived from the original on 2021-01-16. Retrieved 2021-08-25.
- "LaTeX Expression project documentation — LaTeX Expression 0.3.dev documentation". mech.fsv.cvut.cz. Retrieved 2021-08-25.
- "Symbolic Statistics with SymPy". ResearchGate. Retrieved 2021-08-25.
- "Diofant's documentation — Diofant 0.13.0a4.dev13+g8c5685115 documentation". diofant.readthedocs.io. Retrieved 2021-08-25.