Gravity anomaly
The gravity anomaly at a location on the Earth's surface is the difference between the observed value of gravity and the value predicted by a theoretical model. If the Earth were an ideal oblate spheroid of uniform density, then the gravity measured at every point on its surface would be given precisely by a simple algebraic expression. However, the Earth has a rugged surface and non-uniform composition, which distorts its gravitational field. The theoretical value of gravity can be corrected for altitude and the effects of nearby terrain, but it usually still differs slightly from the measured value. This gravity anomaly can reveal the presence of subsurface structures of unusual density. For example, a mass of dense ore below the surface will give a positive anomaly due to the increased gravitational attraction of the ore.
Different theoretical models will predict different values of gravity, and so a gravity anomaly is always specified with reference to a particular model. The Bouguer, free-air, and isostatic gravity anomalies are each based on different theoretical corrections to the value of gravity.
A gravity survey is conducted by measuring the gravity anomaly at many locations in a region of interest, using a portable instrument called a gravimeter. Careful analysis of the gravity data allows geologists to make inferences about the subsurface geology.
Definition
The gravity anomaly is the difference between the observed acceleration of an object in free fall (gravity) near a planet's surface, and the corresponding value predicted by a model of the planet's gravitational field.[1] Typically the model is based on simplifying assumptions, such as that, under its self-gravitation and rotational motion, the planet assumes the figure of an ellipsoid of revolution.[2] Gravity on the surface of this reference ellipsoid is then given by a simple formula which only contains the latitude. For Earth, the reference ellipsoid is the International Reference Ellipsoid, and the value of gravity predicted for points on the ellipsoid is the normal gravity, gn.[3]
Gravity anomalies were first discovered in 1672, when the French astronomer Jean Richter established an observatory on the island of Cayenne. Richter was equipped with a highly precise pendulum clock which had been carefully calibrated at Paris before his departure. However, he found that the clock ran too slowly in Cayenne, compared with the apparent motion of the stars. Fifteen years later, Isaac Newton used his newly formulated universal theory of gravitation to explain the anomaly. Newton showed that the measured value of gravity was affected by the rotation of the Earth, which caused the Earth's equator to bulge out slightly relative to its poles. Cayenne, being nearer the equator than Paris, would be both further from the center of Earth (reducing the Earth's bulk gravitational attraction slightly) and subject to stronger centrifugal acceleration from the Earth's rotation. Both these effects reduce the value of gravity, explaining why Richter's pendulum clock, which depended on the value of gravity, ran too slowly. Correcting for these effects removed most of this anomaly.[4]
To understand the nature of the gravity anomaly due to the subsurface, a number of corrections must be made to the measured gravity value. Different theoretical models will include different corrections to the value of gravity, and so a gravity anomaly is always specified with reference to a particular model. The Bouguer, free-air, and isostatic gravity anomalies are each based on different theoretical corrections to the value of gravity.[5]
The model field and corrections
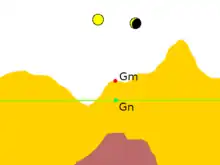
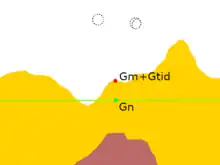
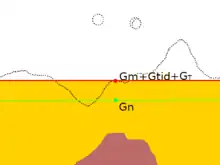
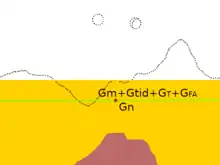
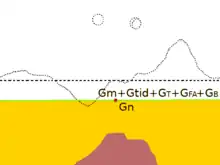
The starting point for the model field is the International Reference Ellipsoid, which gives the normal gravity gn for every point on the Earth's idealized shape. Further refinements of the model field are usually expressed as corrections added to the measured gravity or (equivalently) subtracted from the normal gravity. At a minimum, these include the tidal correction △gtid, the terrain correction △gT, and the free air correction △gFA. Other corrections are added for various gravitational models. The difference between the corrected measured gravity and the normal gravity is the gravity anomaly.[6]
The normal gravity
The normal gravity accounts for the bulk gravitation of the entire Earth, corrected for its idealized shape and rotation. It is given by the formula:
where = 9.780327 m⋅s−2; = 5.30244×10−3; and = −5.8×10−6. This is accurate to 0.1 mgal at any latitude . When greater precision is needed, a more elaborate formula gives the normal gravity with an accuracy of 0.0001 mgal.[7]
The tidal correction
The Sun and Moon create time-dependent tidal forces that affect the measured value of gravity by about 0.3 mgal. Two-thirds of this is from the Moon. This effect is very well understood and can be calculated precisely for a given time and location using astrophysical data and formulas, to yield the tidal correction △gtid.[8]
The terrain correction
The local topography of the land surface affects the gravity measurement. Both terrain higher than the measurement point and valleys lower than the measurement point reduce the measured value of gravity. This is taken into account by the terrain correction △gT. The terrain correction is calculated from knowledge of the local topography and estimates of the density of the rock making up the high ground. In effect, the terrain correction levels the terrain around the measurement point.[9]
The terrain correction must be calculated for every point at which gravity is measured, taking into account every hill or valley whose difference in elevation from the measurement point is greater than about 5% of its distance from the measurement point. This is tedious and time-consuming but necessary for obtaining a meaningful gravity anomaly.[10]
The free-air correction
The next correction is the free-air correction. This takes into account the fact that the measurement is usually at a different elevation than the reference ellipsoid at the measurement latitude and longitude. For a measurement point above the reference ellipsoid, this means that the gravitational attraction of the bulk mass of the earth is slightly reduced. The free-air correction is simply 0.3086 mgal m−1 times the elevation above the reference ellipsoid.[11]
The remaining gravity anomaly at this point in the reduction is called the free-air anomaly. That is, the free-air anomaly is:[12]
Bouguer plate correction
The free-air anomaly does not take into account the layer of material (after terrain leveling) outside the reference ellipsoid. The gravitational attraction of this layer or plate is taken into account by the Bouguer plate correction, which is −0.0419×10−3 ρ h mgal m2 kg−1. The density of crustal rock, ρ, is usually taken to be 2670 kg m3 so the Bouguer plate correction is usually taken as −0.1119 mgal m−1 h. Here h is the elevation above the reference ellipsoid.[13]
The remaining gravity anomaly at this point in the reduction is called the Bouguer anomaly. That is, the Bouguer anomaly is:[12]
Isostatic correction
The Bouguer anomaly is positive over ocean basins and negative over high continental areas. This shows that the low elevation of ocean basins and high elevation of continents is compensated by the thickness of the crust at depth. The higher terrain is held up by the buoyancy of thicker crust "floating" on the mantle.[14]
The isostatic anomaly is defined as the Bouger anomaly minus the gravity anomaly due to the subsurface compensation, and is a measure of the local departure from isostatic equilibrium, due to dynamic processes in the viscous mantle. At the center of a level plateau, it is approximately equal to the free air anomaly.[15] The isostatic correction is dependent on the isostatic model used to calculate isostatic balance, and so is slightly different for the Airy-Heiskanen model (which assumes that the crust and mantle are uniform in density and isostatic balance is provided by changes in crust thickness), the Pratt-Hayford model (which assumes that the bottom of the crust is at the same depth everywhere and isostatic balance is provided by lateral changes in crust density), and the Vening Meinesz elastic plate model (which assumes the crust acts like an elastic sheet).[16]
Forward modelling is the process of computing the detailed shape of the compensation required by a theoretical model and using this to correct the Bouguer anomaly to yield an isostatic anomaly.[17]
Causes
Lateral variations in gravity anomalies are related to anomalous density distributions within the Earth. Local measurements of the gravity of Earth help us to understand the planet's internal structure.
Regional causes
The Bouguer anomaly over continents is generally negative, especially over mountain ranges.[18] For example, typical Bouguer anomalies in the Central Alps are −150 milligals.[19] By contrast, the Bouguer anomaly is positive over oceans. These anomalies reflect the varying thickness of the Earth's crust. The higher continental terrain is supported by thick, low-density crust that "floats" on the denser mantle, while the ocean basins are floored by much thinner oceanic crust. The free-air and isostatic anomalies are small near the centers of ocean basins or continental plateaus, showing that these are approximately in isostatic equilibrium. The gravitational attraction of the high terrain is balanced by the reduced gravitational attraction of its underlying low-density roots. This brings the free-air anomaly, which omits the correction terms for either, close to zero. The isostatic anomaly includes correction terms for both effects, which reduces it nearly to zero as well. The Bouguer anomaly includes only the negative correction for the high terrain and so is strongly negative.[18]
More generally, the Airy isostatic anomaly is zero over regions where there is complete isostatic compensation. The free-air anomaly is also close to zero except near boundaries of crustal blocks. The Bouger anomaly is very negative over elevated terrain. The opposite is true for the theoretical case of terrain that is completely uncompensated: The Bouger anomaly is zero while the free-air and Airy isostatic anomalies are very positive.[15]
The Bouger anomaly map of the Alps shows additional features besides the expected deep mountain roots. A positive anomaly is associated with the Ivrea body, a wedge of dense mantle rock caught up by an ancient continental collision. The low-density sediments of the Molasse basin produce a negative anomaly. Larger surveys across the region provide evidence of a relict subduction zone.[20] Negative isostatic anomalies in Switzerland correlate with areas of active uplift, while positive anomalies are associated with subsidence.[21]
Over mid-ocean ridges, the free-air anomalies are small and correlate with the ocean bottom topography. The ridge and its flanks appear to be fully isostatically compensated. There is a large Bouger positive, of over 350 mgal, beyond 1,000 kilometers (620 mi) from the ridge axis, which drops to 200 over the axis. This is consistent with seismic data and suggests the presence of a low-density magma chamber under the ridge axis.[22]
There are intense isostatic and free-air anomalies along island arcs. These are indications of strong dynamic effects in subduction zones. The free-air anomaly is around +70 mgal along the Andes coast, and this is attributed to the subducting dense slab. The trench itself is very negative,[23] with values more negative than −250 mgal. This arises from the low-density ocean water and sediments filling the trench.[24]
Gravity anomalies provide clues on other processes taking place deep in the lithosphere. For example, the formation and sinking of a lithospheric root may explain negative isostatic anomalies in eastern Tien Shan.[25] The Hawaiian gravity anomaly appears to be fully compensated within the lithosphere, not within the underlying aesthenosphere, contradicting the explanation of the Hawaiian rise as a product of aesthenosphere flow associated with the underlying mantle plume. The rise may instead be a result of lithosphere thinning: The underlying aesthenosphere is less dense than the lithosphere and it rises to produce the swell. Subsequent cooling thickens the lithosphere again and subsidence takes place.[26]
Local anomalies
Local anomalies are used in applied geophysics. For example, a local positive anomaly may indicate a body of metallic ores. Salt domes are typically expressed in gravity maps as lows, because salt has a low density compared to the rocks the dome intrudes.[27]
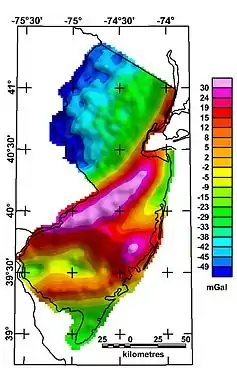
At scales between entire mountain ranges and ore bodies, Bouguer anomalies may indicate rock types. For example, the northeast-southwest trending high across central New Jersey represents a graben of Triassic age largely filled with dense basalts.[28]
Satellite measurements

Currently, the static and time-variable Earth's gravity field parameters are being determined using modern satellite missions, such as GOCE, CHAMP, Swarm, GRACE and GRACE-FO.[29][30] The lowest-degree parameters, including the Earth's oblateness and geocenter motion are best determined from Satellite laser ranging.[31]
Large-scale gravity anomalies can be detected from space, as a by-product of satellite gravity missions, e.g., GOCE. These satellite missions aim at the recovery of a detailed gravity field model of the Earth, typically presented in the form of a spherical-harmonic expansion of the Earth's gravitational potential, but alternative presentations, such as maps of geoid undulations or gravity anomalies, are also produced.
The Gravity Recovery and Climate Experiment (GRACE) consists of two satellites that can detect gravitational changes across the Earth. Also these changes can be presented as gravity anomaly temporal variations. The Gravity Recovery and Interior Laboratory (GRAIL) also consisted of two spacecraft orbiting the Moon, which orbited for three years before their deorbit in 2015.See also
References
- Jackson, Julia A., ed. (1997). "gravity anomaly". Glossary of geology (Fourth ed.). Alexandria, Virginia: American Geological Institute. ISBN 0922152349.
- Lowrie, William (2007). "2". Fundamentals of geophysics (2nd ed.). Cambridge: Cambridge University Press. ISBN 978-1-60119-744-3.
- Lowrie 2007, p. 65.
- Lowrie 2007, p. 44.
- Allaby, Michael (2013). "gravity anomaly". A dictionary of geology and earth sciences (Fourth ed.). Oxford: Oxford University Press. ISBN 9780199653065.
- Lowrie 2007, pp. 77–78.
- Lowrie 2007, pp. 65–66.
- Lowrie 2007, p. 54.
- Lowrie 2007, p. 77.
- Lowrie 2007, p. 79.
- Lowrie 2007, pp. 79–80.
- Lowrie 2007, pp. 83–84.
- Lowrie 2007, p. 80.
- Kearey, P.; Klepeis, K.A.; Vine, F.J. (2009). Global tectonics (3rd ed.). Oxford: Wiley-Blackwell. p. 42. ISBN 9781405107778.
- Kearey, Klepeis & Vine 2009, pp. 45–48.
- Lowrie 2007, pp. 103–104.
- Kearey, Klepeis & Vine 2009, p. 46.
- Lowrie 2007, p. 95.
- Werner, Dietrich; Kissling, Eduard (August 1985). "Gravity anomalies and dynamics of the Swiss Alps". Tectonophysics. 117 (1–2): 97–108. Bibcode:1985Tectp.117...97W. doi:10.1016/0040-1951(85)90239-2.
- Lowrie 2007, p. 97.
- Lowrie 2007, p. 103–105.
- Lowrie 2007, pp. 97–99.
- Monroe, James S.; Wicander, Reed (1992). Physical geology : exploring the Earth. St. Paul: West Pub. Co. p. 326. ISBN 0314921958.
- Lowrie 2007, p. 99.
- Burov, E. V.; Kogan, M. G.; Lyon-Caen, Hélène; Molnar, Peter (1 January 1990). "Gravity anomalies, the deep structure, and dynamic processes beneath the Tien Shan". Earth and Planetary Science Letters. 96 (3): 367–383. Bibcode:1990E&PSL..96..367B. doi:10.1016/0012-821X(90)90013-N.
- Detrick, Robert S.; Crough, S. Thomas (1978). "Island subsidence, hot spots, and lithospheric thinning". Journal of Geophysical Research. 83 (B3): 1236. Bibcode:1978JGR....83.1236D. doi:10.1029/JB083iB03p01236.
- Monroe & Wicander 1992, pp. 302–303.
- Herman, G.C.; Dooley, J.H.; Monteverde, D.H. (2013). "Structure of the CAMP bodies and positive Bouger gravity anomalies of the New York Recess". Igneous processes during the assembly and breakup of Pangaea: Northern New Jersey and New York City: 30th Annual Meeting of the Geological Association of New Jersey. New York: College of Staten Island. pp. 103–142. Retrieved 29 January 2022.
- Meyer, Ulrich; Sosnica, Krzysztof; Arnold, Daniel; Dahle, Christoph; Thaller, Daniela; Dach, Rolf; Jäggi, Adrian (22 April 2019). "SLR, GRACE and Swarm Gravity Field Determination and Combination". Remote Sensing. 11 (8): 956. Bibcode:2019RemS...11..956M. doi:10.3390/rs11080956.
- Tapley, Byron D.; Watkins, Michael M.; Flechtner, Frank; Reigber, Christoph; Bettadpur, Srinivas; Rodell, Matthew; Sasgen, Ingo; Famiglietti, James S.; Landerer, Felix W.; Chambers, Don P.; Reager, John T.; Gardner, Alex S.; Save, Himanshu; Ivins, Erik R.; Swenson, Sean C.; Boening, Carmen; Dahle, Christoph; Wiese, David N.; Dobslaw, Henryk; Tamisiea, Mark E.; Velicogna, Isabella (May 2019). "Contributions of GRACE to understanding climate change". Nature Climate Change. 9 (5): 358–369. Bibcode:2019NatCC...9..358T. doi:10.1038/s41558-019-0456-2. PMC 6750016. PMID 31534490.
- Sośnica, Krzysztof; Jäggi, Adrian; Meyer, Ulrich; Thaller, Daniela; Beutler, Gerhard; Arnold, Daniel; Dach, Rolf (October 2015). "Time variable Earth's gravity field from SLR satellites". Journal of Geodesy. 89 (10): 945–960. Bibcode:2015JGeod..89..945S. doi:10.1007/s00190-015-0825-1.
Further reading
- Heiskanen, Weikko Aleksanteri; Moritz, Helmut (1967). Physical Geodesy. W.H. Freeman.
