Gyroelongated bipyramid
In geometry, the gyroelongated bipyramids are an infinite set of polyhedra, constructed by elongating an n-gonal bipyramid by inserting an n-gonal antiprism between its congruent halves.
| Gyroelongated bipyramid | |
|---|---|
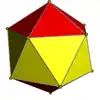 The pentagonal gyroelongated bipyramid is the regular icosahedron. | |
| Faces | 4n triangles |
| Edges | 6n |
| Vertices | 2n + 2 |
| Symmetry group | Dnd, [2+,2n], (2*n), order 4n |
| Rotation group | Dn, [2,n]+, (22n), order 2n |
| Dual polyhedron | truncated trapezohedra |
| Properties | convex |
Forms
Two members of the set can be deltahedra, that is, constructed entirely of equilateral triangles: the gyroelongated square bipyramid, a Johnson solid, and the icosahedron, a Platonic solid. The gyroelongated triangular bipyramid can be made with equilateral triangles, but is not a deltahedron because it has coplanar faces, i.e. is not strictly convex. With pairs of triangles merged into rhombi, it can be seen as a trigonal trapezohedron. The other members can be constructed with isosceles triangles.
| n | 3 | 4 | 5 | 6 | n |
|---|---|---|---|---|---|
| Type | Coplanar | Equilateral | Regular | Coplanar | |
| Shape | Gyroelongated triangular bipyramid | Gyroelongated square bipyramid | Gyroelongated pentagonal bipyramid (icosahedron) |
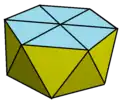
Gyroelongated hexagonal bipyramid | Gyroelongated bipyramid |
| Image | 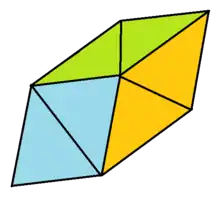 |
 |
 |
 |
|
| Faces | 12 | 16 | 20 | 24 | 4n |
| Dual | Triangular truncated trapezohedron | Square truncated trapezohedron | Pentagonal truncated trapezohedron (Dodecahedron) |
Hexagonal truncated trapezohedron | Truncated trapezohedra |
External links
- Conway Notation for Polyhedra Try: "knAn", where n=4,5,6... example "k5A5" is an icosahedron.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.