Harmonic major scale

In music theory, the harmonic major scale is a musical scale found in some music from the common practice era and now used occasionally, most often in jazz. In George Russell's Lydian Chromatic Concept it is the fifth mode (V) of the Lydian Diminished scale.[1] It corresponds to the Raga Sarasangi in Indian Carnatic music.

Harmonic major scale on C Play^ⓘ.

It can be considered a major scale with the sixth degree lowered, Ionian ♭6,[2] or the harmonic minor scale with the third degree raised. The intervals between the notes of a harmonic major scale follow the sequence below:

whole, whole, half, whole, half, augmented second, half

The harmonic major scale may be used to construct the following chords, which also may be thought of as borrowed from the parallel minor: the dominant minor ninth chord, the fully diminished seventh leading tone chord, the supertonic diminished triad, the supertonic half-diminished seventh chord, and the minor subdominant. It also contains an augmented triad.

V7♭9: G-B–D–F–A♭ viio7: B–D–F–A♭ iio: D–F–A♭ iiø7: D–F–A♭–C iv: F–A♭–C ♭VI+: A♭–C–E

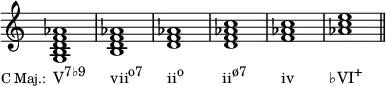The harmonic major scale has its own set of modes, distinct from the harmonic minor, melodic minor, and major modes, depending on which note serves as the tonic. Below are the mode names, their degrees, and the following seventh chords that can be built using each modal tonic or degree of the parent mode as the root: a major seventh chord, a half-diminished seventh chord, a minor seventh chord, a minor major seventh chord, a dominant seventh chord, an augmented major seventh chord, and a diminished seventh chord. Harmonic minor contains the same types of seventh chords, but in a different order.

Mode	I	II	III	IV	V	VI	VII
Name	Harmonic Major	Locrian ♮2 ♮6 / Dorian ♭5	Altered Dominant ♮5 / Phrygian ♭4	Melodic Minor ♯4 / Lydian ♭3	Mixolydian ♭2	Lydian Augmented ♯2	Locrian 7
Notes	1 2 3 4 5 ♭6 7	1 2 ♭3 4 ♭5 6 ♭7	1 ♭2 ♭3 ♭4 5 ♭6 ♭7	1 2 ♭3 ♯4 5 6 7	1 ♭2 3 4 5 6 ♭7	1 ♯2 3 ♯4 ♯5 6 7	1 ♭2 ♭3 4 ♭5 ♭6 7
Triads	C	Do	Em (or E since the ♭4 can be respelled as 3 (enharmonic equivalent) ; 1, ♭4, 5)	Fm	G	A♭+	Bo
Seventh Chords	CΔ	Dø7	E–7 or E7	F–Δ	G7	A♭+Δ	Bo7

A progression in harmonic major Play^ⓘ.

For example, a D-flat major scale consists of the notes: D♭ E♭ F G♭ A♭ B♭ C; whereas a D-flat harmonic major scale consists of the notes: D♭ E♭ F G♭ A♭ B C. Notice the sixth note in the sequence is lowered, from B♭ to B. The C-sharp harmonic major scale can also be obtained from the C-sharp harmonic minor scale, which is C♯ D♯ E F♯ G♯ A B♯, by raising the E to E♯. The C harmonic major scale may be derived from the F melodic minor scale with a raised fourth: F G A♭ B C D E.[3]

Harmonic major scale on C

The harmonic major scale may also be considered a synthetic scale, primarily used for implying and relating to various altered chords, with major and minor qualities in each tetrachord.[4] Thus the musical effect of the harmonic major scale is a sound intermediate between harmonic minor and diatonic major, and partaking of both. The harmonic major scale may be used in any system of meantone tuning, such as 19 equal temperament or 31 equal temperament, as well as 12 equal temperament.

One interesting property of this scale is that for any diatonic scale, there is a relative major or minor mode, and if each of these is made harmonic major or harmonic minor, the accidental required in each "harmonic" scale is actually the same note spelled enharmonically. For example, the added accidental in C harmonic major, A♭ (shown in first image), is enharmonically equivalent to the added accidental, G♯, in the relative harmonic minor of C major, A harmonic minor. Also, another enharmonic mode of the scale is the Jazz Minor b5 scale (Jeths's mode) (B in C Harmonic Major, Cb in F Jazz Minor b5).

Harmonic major scale in thirds

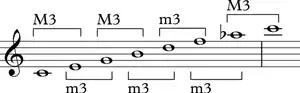
Like the familiar major, melodic minor, and harmonic minor scales, the harmonic major scale has the diatonic thirds property, which means that the interval between notes two steps apart (e.g. the second and fourth note, or the third and fifth note, etc..) are separated by a major or minor third, i.e. the interval of three or four semitones.[5] There are only seven such scales in equal temperament, including whole tone, hexatonic from alternating minor thirds and semitones, diatonic, ascending melodic minor, harmonic minor, harmonic major, and octatonic (diminished). This property implies that chords formed by taking every other note from some consecutive subset of the scale are triadic, raising the possibility of using tertian harmony together with melodic material from such a scale.

The harmonic major scale is also one of the five proper seven-note scales of equal temperament. Like five of those other six scales, it is a complete circle of thirds; starting from the tonic the pattern is MmmmMMm, where M is a major third and m is a minor third.

Harmonic major is not commonly taught as a tonality, so chords borrowed from this diatonic tonality are not recognized as readily as those from the tonalities of major, harmonic minor, and melodic minor. Many popular songs have borrowed chords from the tonality of harmonic major but have not been recognized as doing so. Examples are 'After You've Gone', 'Blackbird', 'Sleep Walk', 'Dream A Little Dream Of Me'.