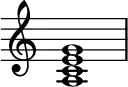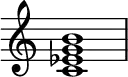Minor seventh chord

minor/minor seventh chord
Component intervals from root
	minor seventh
	perfect fifth
	minor third
	root
Tuning
	10:12:15:18[1]
Forte no. / Complement
	4-26 / 8-26

In music, a minor seventh chord is a seventh chord composed of a root note, together with a minor third, a perfect fifth, and a minor seventh (1, ♭3, 5, ♭7).

For example, the minor seventh chord built on A, commonly written as A–⁷, has pitches A-C-E-G:

${ \new Staff \with{ \magnifyStaff #1.5 } \relative c' { \override Score.TimeSignature #'stencil = ##f <a c e g>1 } }$

Minor/minor seventh chord

A seventh chord with a minor third, perfect fifth, and minor seventh is commonly called a minor seventh chord, but also sometimes a minor/minor seventh chord to distinguish it from the minor/major seventh chord discussed below. It can be represented as either as m⁷ or −⁷, or in integer notation, {0, 3, 7, 10}.

This chord occurs on different scale degrees in different diatonic scales:

In a major scale, it is on the supertonic, mediant, and submediant degrees (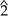, , 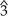and 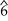).[2] This is why the ii in a ii–V–I turnaround is a minor seventh chord (ii⁷).

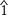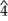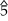In a natural minor scale, it is on the tonic, subdominant, and dominant degrees (, , and ).[3]
In a harmonic minor scale, it is only on the subdominant degree (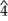).[3]
In an ascending melodic minor scale, it is only on the supertonic degree (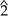).[3]

Example of tonic minor seventh chords include LaBelle's "Lady Marmalade", Roberta Flack's "Killing Me Softly with His Song", The Doobie Brothers' "Long Train Runnin'", Chic's "Le Freak", Lipps Inc.'s "Funkytown", and the Eagles' "One Of These Nights".[4]

The major sixth chord (major triad with an added major sixth) is an inversion of this chord.

Minor/major seventh chord

When the seventh note is a major seventh above the root, it is called a minor/major seventh chord. For example, the minor/major seventh chord built on C, commonly written as Cm^M7, has pitches C–E♭–G–B:

${ \new Staff \with{ \magnifyStaff #1.5 } \relative c' { \override Score.TimeSignature #'stencil = ##f <c es g b>1 } }$

Its harmonic function is similar to that of a "normal" minor seventh, as is the minor seven flat five or half-diminished chord – but in each case, the altered tone (seventh or fifth, respectively) creates a different feeling which is exploited in modulations and to use leading-tones.

Minor seventh as virtual augmented sixth chord

The minor seventh chord may also have its interval of minor seventh (between root and seventh degree, i.e.: C–B♭ in C–E♭–G–B♭) rewritten as an augmented sixth C–E♭–G–A♯.[5] Rearranging and transposing, this gives A♭–C♭–E♭–F♯, a virtual minor version of the German augmented sixth chord.[6] Again like the typical augmented sixth, this enharmonic interpretation gives on a resolution irregular for the minor seventh but normal for the augmented sixth chord, where the 2 voices at the enharmonic major second converge to unison or diverge to octave.[7]

Minor seventh chord table

Chord	Root	Minor third	Perfect fifth	Minor seventh
Cm⁷	C	E♭	G	B♭
C♯m⁷	C♯	E	G♯	B
D♭m⁷	D♭	F♭ (E)	A♭	C♭ (B)
Dm⁷	D	F	A	C
D♯m⁷	D♯	F♯	A♯	C♯
E♭m⁷	E♭	G♭	B♭	D♭
Em⁷	E	G	B	D
Fm⁷	F	A♭	C	E♭
F♯m⁷	F♯	A	C♯	E
G♭m⁷	G♭	B 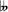(A)	D♭	F♭ (E)
Gm⁷	G	B♭	D	F
G♯m⁷	G♯	B	D♯	F♯
A♭m⁷	A♭	C♭ (B)	E♭	G♭
Am⁷	A	C	E	G
A♯m⁷	A♯	C♯	E♯ (F)	G♯
B♭m⁷	B♭	D♭	F	A♭
Bm⁷	B	D	F♯	A

The just minor seventh chord is tuned in the ratios 10:12:15:18.[8] Play^ⓘ This may be found on iii, vi, and vii.[9] Another tuning may be in the ratios 48:40:32:27.[10] Play^ⓘ

Minor seventh chords for guitar

In standard tuning, the left is the low E string, the number is the fret, and x means mute the string.

Am⁷: x02010
Bm⁷: xx7777
Cm⁷: xx1313
Dm⁷: xx0211
Em⁷: xx0987
Fm⁷: xx1111
Gm⁷: xx3333[11] [12] [13]

References

Shirlaw, Matthew (1900). The Theory of Harmony, p.86. ISBN 978-1-4510-1534-8.
Benward & Saker (2003), p.229.
Benward & Saker (2003). Music: In Theory and Practice, Vol. I, p.230. Seventh Edition. ISBN 978-0-07-294262-0.
Stephenson, Ken (2002). What to Listen for in Rock: A Stylistic Analysis, p.83. ISBN 978-0-300-09239-4.
Ouseley, Frederick. A. Gore (1868). A Treatise on Harmony, pg. 137, Oxford, Clarendon Press.
Ouseley, Frederick. A. Gore (1868). A Treatise on Harmony, pg. 143ff, Oxford, Clarendon Press.
Christ, William (1966). Materials and Structure of Music, v.2, p. 154. Englewood Cliffs: Prentice-Hall. LOC 66-14354.
David Wright (2009). Mathematics and Music, p.141. ISBN 978-0-8218-4873-9.
Wright, David (2009). Mathematics and Music, p.140-41. ISBN 978-0-8218-4873-9.
François-Joseph Fétis and Mary I. Arlin (1994). Esquisse de l'histoire de l'harmonie, p.97n55. ISBN 0-945193-51-3.
"Reverse Guitar Chord Name Finder With Sound, Vertical Fretboard".
"Minor 7th Chords".
"Music | audiopologie". Archived from the original on 2017-12-10. Retrieved 2017-12-17.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Shirlaw, Matthew (1900). The Theory of Harmony, p.86. ISBN 978-1-4510-1534-8.

[2] Benward & Saker (2003), p.229.

[B&S-3] Benward & Saker (2003). Music: In Theory and Practice, Vol. I, p.230. Seventh Edition. ISBN 978-0-07-294262-0.

[Stephenson-4] Stephenson, Ken (2002). What to Listen for in Rock: A Stylistic Analysis, p.83. ISBN 978-0-300-09239-4.

[5] Ouseley, Frederick. A. Gore (1868). A Treatise on Harmony, pg. 137, Oxford, Clarendon Press.

[6] Ouseley, Frederick. A. Gore (1868). A Treatise on Harmony, pg. 143ff, Oxford, Clarendon Press.

[7] Christ, William (1966). Materials and Structure of Music, v.2, p. 154. Englewood Cliffs: Prentice-Hall. LOC 66-14354.

[8] David Wright (2009). Mathematics and Music, p.141. ISBN 978-0-8218-4873-9.

[9] Wright, David (2009). Mathematics and Music, p.140-41. ISBN 978-0-8218-4873-9.

[10] François-Joseph Fétis and Mary I. Arlin (1994). Esquisse de l'histoire de l'harmonie, p.97n55. ISBN 0-945193-51-3.

[11] "Reverse Guitar Chord Name Finder With Sound, Vertical Fretboard".

[12] "Minor 7th Chords".

[13] "Music | audiopologie". Archived from the original on 2017-12-10. Retrieved 2017-12-17.