Highest median voting rules

Let ${\displaystyle {\mathcal {C}}}$ be the set of candidates, ${\displaystyle {\mathcal {V}}}$ the set of voters, and ${\displaystyle {\mathcal {G}}}$ an ordered finite set of ratings (e.g. the following ratings: "Very good", "Good", "Average", "Bad").

For any candidate ${\displaystyle c\in {\mathcal {C}}}$, ${\displaystyle c}$'s median rating ${\displaystyle \alpha _{c}\in {\mathcal {G}}}$ is the median rating among the ratings that ${\displaystyle c}$ received from voters. For example, if there are ten voters and if candidate ${\displaystyle A}$ receives three ratings "Good", six ratings "Average", and one rating "Bad", its median rating ${\displaystyle \alpha _{A}}$ is "Average".

If, for any candidate ${\displaystyle i\neq c}$, ${\displaystyle \alpha _{i}<\alpha _{c}}$, then ${\displaystyle c}$ obtained a higher median rating than all other candidates, and ${\displaystyle c}$ is elected, regardless of which highest median rule was chosen.

When different candidates share the same median rating, a tie-breaking rule is required. This tie-breaking rule characterizes the highest median rule at use.

Tie-breaking rules often make use of two additional statistics about a candidate ${\displaystyle c}$'s ratings:[1]

• The share of proponents to ${\displaystyle c}$, noted ${\displaystyle p_{c}}$, which is the share of voters attributing to ${\displaystyle c}$ a rating greater than its median ${\displaystyle \alpha _{c}}$. In the example above, the three ratings "Good" are above ${\displaystyle A}$'s median "Average", so ${\displaystyle p_{A}={\frac {3}{10}}}$.
• The share of opponents to ${\displaystyle c}$, noted ${\displaystyle q_{c}}$, which is the share of voters attributing to ${\displaystyle c}$ a rating lesser than its median ${\displaystyle \alpha _{c}}$. In the example above, this correspond to the rating "Bad", so ${\displaystyle q_{A}={\frac {1}{10}}}$.

Examples

Example of vote outcome where each choice (or candidate) A, B, C or D wins according to one of the four tie-breaking rules studied: respectively typical judgment (${\displaystyle d}$), central judgment (${\displaystyle s}$), usual judgment (${\displaystyle n}$), and majority judgment (${\displaystyle mj}$).[1]

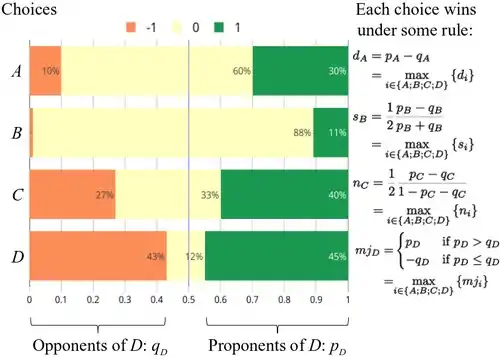
• The typical judgment orders the candidates according to the largest difference between their share of proponents and opponents, i.e. according to the formula:[1] ${\displaystyle d=\alpha +p-q}$ (the indices ${\displaystyle c}$ are omitted for simplicity). In the above example, and identifying "Average" with the grade ${\displaystyle 0}$, we have ${\displaystyle d_{A}=0+0.3-0.1=+0.2}$.
• The usual judgment is the rule said to offer the best properties,[1] but it orders the candidates according to a slightly more complex formula: ${\displaystyle n=\alpha +{\frac {1}{2}}{\frac {p-q}{1-p-q}}}$; compared to the typical judgment, this leads to a more prominent score difference in small changes of number of proponents and opponents when the median share is low, as the equation approaches 0.5 both as either ${\displaystyle p}$ or ${\displaystyle q}$ approaches 0.5 (neither can actually be 0.5, as the median lies at the halfway point by definition).
• The central judgment orders the candidates according to the highest ratio between the shares of proponents and opponents, that is to say according to the formula: ${\displaystyle s=\alpha +{\frac {1}{2}}{\frac {p-q}{p+q+\epsilon }}}$ (where ${\displaystyle \epsilon }$ is an arbitrarily small number that simply allows the denominator to remain positive); compared to the typical judgment, this leads to a more prominent score difference in small changes of number of proponents and opponents when the median share is high, as the equation approaches 0.5 both as either ${\displaystyle p}$ or ${\displaystyle q}$ approaches 0.5. In fact, the usual judgment ${\displaystyle U(p,q)}$ is equivalent to the central judgment ${\displaystyle C(0.5-q,0.5-p)}$.
• The majority judgment considers the candidate who is closest to having a rating other than its median and breaks the tie based on that rating. This is equivalent to ordering the candidates according to their score ${\displaystyle mj}$,[1] defined by the following formula (the symbol ${\displaystyle \mathbf {1} }$ denotes the indicator function) : ${\displaystyle mj=\alpha +\mathbf {1} _{p>q}p-\mathbf {1} _{p\leq q}q}$.
• The Bucklin rules are close to the highest median rules but have been developed for ranked rules. They order the candidates according to the formula: ${\displaystyle b=\alpha -q}$. In a ranked rule, this is equivalent to counting first choice votes first. If one candidate has a majority, that candidate wins. Otherwise the second choices are added to the first choices. If a candidate with a majority vote is found, the winner is the candidate with the most votes accumulated. Lower rankings are added as needed.[2]
• Approval voting corresponds to the degenerate case where there are only two possible ratings: approval and disapproval. In this particular case, all the tie-breaking rules are equivalent, and the Condorcet criterion is satisfied.[3]

• Cardinal voting
• Majority judgment
• Bucklin voting
• Electoral System
• Comparison of electoral systems

• Baujard, Antoinette; Gavrel, Frédéric; Igersheim, Herrade; Laslier, Jean-François; Lebon, Isabelle (September 2017). "How voters use grade scales in evaluative voting" (PDF). European Journal of Political Economy. 55: 14–28. doi:10.1016/j.ejpoleco.2017.09.006. ISSN 0176-2680.

• R package implementing different highest median rules, as well as range voting: HighestMedianRules.