Integral of the secant function
In calculus, the integral of the secant function can be evaluated using a variety of methods and there are multiple ways of expressing the antiderivative, all of which can be shown to be equivalent via trigonometric identities,

| Part of a series of articles about |
| Calculus |
|---|
This formula is useful for evaluating various trigonometric integrals. In particular, it can be used to evaluate the integral of the secant cubed, which, though seemingly special, comes up rather frequently in applications.[1]
The definite integral of the secant function starting from is the inverse Gudermannian function, For numerical applications, all of the above expressions result in loss of significance for some arguments. An alternative expression in terms of the inverse hyperbolic sine arsinh is numerically well behaved for real arguments :[2]
The integral of the secant function was historically one of the first integrals of its type ever evaluated, before most of the development of integral calculus. It is important because it is the vertical coordinate of the Mercator projection, used for marine navigation with constant compass bearing.
Proof that the different antiderivatives are equivalent
Trigonometric forms
Three common expressions for the integral of the secant,
are equivalent because
Proof: we can separately apply the tangent half-angle substitution to each of the three forms, and show them equivalent to the same expression in terms of Under this substitution and
First,
Second,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/en.wikipedia.org/v1/":): {\displaystyle \begin{align} \bigl|\sec\theta + \tan\theta\,\bigr| &= \left|\frac1{\cos\theta} + \frac{\sin\theta}{\cos\theta}\right| = \left|\frac{1 + t^2}{1 - t^2} + \frac{2t}{1 - t^2}\right| = \left|\frac{(1 + t)^2}{(1 + t)(1 - t)}\right| \\[5mu] &= \left|\frac{1 + t}{1 - t}\right|. \end{align}}
Third, using the tangent addition identity
So all three expressions describe the same quantity.
The conventional solution for the Mercator projection ordinate may be written without the absolute value signs since the latitude lies between and ,
Hyperbolic forms
Let
Therefore,
History
The integral of the secant function was one of the "outstanding open problems of the mid-seventeenth century", solved in 1668 by James Gregory.[3] He applied his result to a problem concerning nautical tables.[1] In 1599, Edward Wright evaluated the integral by numerical methods – what today we would call Riemann sums.[4] He wanted the solution for the purposes of cartography – specifically for constructing an accurate Mercator projection.[3] In the 1640s, Henry Bond, a teacher of navigation, surveying, and other mathematical topics, compared Wright's numerically computed table of values of the integral of the secant with a table of logarithms of the tangent function, and consequently conjectured that[3]
This conjecture became widely known, and in 1665, Isaac Newton was aware of it.[5]
Evaluations
By a standard substitution (Gregory's approach)
A standard method of evaluating the secant integral presented in various references involves multiplying the numerator and denominator by sec θ + tan θ and then using the substitution u = sec θ + tan θ. This substitution can be obtained from the derivatives of secant and tangent added together, which have secant as a common factor.[6]
Starting with
adding them gives
The derivative of the sum is thus equal to the sum multiplied by sec θ. This enables multiplying sec θ by sec θ + tan θ in the numerator and denominator and performing the following substitutions:
The integral is evaluated as follows:
as claimed. This was the formula discovered by James Gregory.[1]
By partial fractions and a substitution (Barrow's approach)
Although Gregory proved the conjecture in 1668 in his Exercitationes Geometricae,[7] the proof was presented in a form that renders it nearly impossible for modern readers to comprehend; Isaac Barrow, in his Lectiones Geometricae of 1670,[8] gave the first "intelligible" proof, though even that was "couched in the geometric idiom of the day."[3] Barrow's proof of the result was the earliest use of partial fractions in integration.[3] Adapted to modern notation, Barrow's proof began as follows:
Substituting u = sin θ, du = cos θ dθ, reduces the integral to
Therefore,
as expected. Taking the absolute value is not necessary because and are always non-negative for real values of
Standard
Under the tangent half-angle substitution [9]
Therefore the integral of the secant function is
as before.
Non-standard
The integral can also be derived by using a somewhat non-standard version of the tangent half-angle substitution, which is simpler in the case of this particular integral, published in 2013,[10] is as follows:
Substituting:
By two successive substitutions
The integral can also be solved by manipulating the integrand and substituting twice. Using the definition sec θ = 1/cos θ and the identity cos2 θ + sin2 θ = 1, the integral can be rewritten as
Substituting u = sin θ, du = cos θ dθ reduces the integral to
The reduced integral can be evaluated by substituting u = tanh t, du = sech2 t dt, and then using the identity 1 − tanh2 t = sech2 t.
The integral is now reduced to a simple integral, and back-substituting gives
which is one of the hyperbolic forms of the integral.
A similar strategy can be used to integrate the cosecant, hyperbolic secant, and hyperbolic cosecant functions.
Other hyperbolic forms
It is also possible to find the other two hyperbolic forms directly, by again multiplying and dividing by a convenient term:
where stands for because Substituting u = tan θ, du = sec2 θ dθ, reduces to a standard integral:
where sgn is the sign function.
Likewise:
Substituting u = |sec θ|, du = |sec θ| tan θ dθ, reduces to a standard integral:
Using complex exponential form
Under the substitution
So the integral can be solved as:
Because the constant of integration can be anything, the additional constant term can be absorbed into it. Finally, if theta is real-valued, we can indicate this with absolute value brackets in order to get the equation into its most familiar form:
Gudermannian and Lambertian
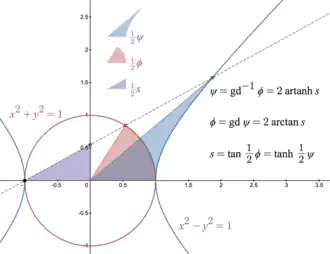
The integral of the hyperbolic secant function defines the Gudermannian function:
The integral of the secant function defines the Lambertian function, which is the inverse of the Gudermannian function:
These functions are encountered in the theory of map projections: the Mercator projection of a point on the sphere with longitude λ and latitude ϕ may be written[11] as:
See also
Notes
- Stewart, James (2012). "Section 7.2: Trigonometric Integrals". Calculus - Early Transcendentals. Cengage Learning. pp. 475–6. ISBN 978-0-538-49790-9.
- For example this form is used in Karney, Charles F.F. (2011). "Transverse Mercator with an accuracy of a few nanometers". Journal of Geodesy. 85: 475–485.
- V. Frederick Rickey and Philip M. Tuchinsky, An Application of Geography to Mathematics: History of the Integral of the Secant in Mathematics Magazine, volume 53, number 3, May 1980, pages 162–166.
- Edward Wright, Certaine Errors in Navigation, Arising either of the ordinaire erroneous making or vsing of the sea Chart, Compasse, Crosse staffe, and Tables of declination of the Sunne, and fixed Starres detected and corrected, Valentine Simms, London, 1599.
- H. W. Turnbull, editor, The Correspondence of Isaac Newton, Cambridge University Press, 1959–1960, volume 1, pages 13–16 and volume 2, pages 99–100.
D. T. Whiteside, editor, The Mathematical Papers of Isaac Newton, Cambridge University Press, 1967, volume 1, pages 466–467 and 473–475.
-
Feldman, Joel. "Integration of sec x and sec3 x" (PDF). University of British Columbia Mathematics Department.
"Integral of Secant". MIT OpenCourseWare.
- Gregory, James (1668). "Analogia Inter Lineam Meridianam Planispherii Nautici & Tangentes Artificiales Geometricè Demonstrata, &c." [Analogy Between the Meridian Line of the Nautical Planisphere & Artificial Tangents Geometrically Demonstrated, &c.]. Exercitationes Geometricae [Geometrical Exercises] (in Latin). Moses Pitt. pp. 14–24.
- Barrow, Isaac (1674) [1670]. "Lectiones geometricae: XII, Appendicula I". Lectiones Opticae & Geometricae (in Latin). Typis Guilielmi Godbid. pp. 110–114. In English, "Lecture XII, Appendix I". The Geometrical Lectures of Isaac Barrow. Translated by Child, James Mark. Open Court. 1916. pp. 165–169.
- Stewart, James (2012). "Section 7.4: Integration of Rational Functions by Partial Fractions". Calculus: Early Transcendentals (7th ed.). Belmont, CA, USA: Cengage Learning. pp. 493. ISBN 978-0-538-49790-9.
- Hardy, Michael (2013). "Efficiency in Antidifferentiation of the Secant Function". American Mathematical Monthly. 120 (6): 580.
- Lee, Laurence Patrick (1976). Conformal Projections Based on Elliptic Functions. Cartographica Monograph. Vol. 16. University of Toronto Press. ISBN 9780919870161.
References
- Maseres, Francis, ed. (1791). Scriptores Logarithmici; Or, A Collection of Several Curious Tracts on the Nature and Construction of Logarithms. Vol. 2. J. Davis.
- Strauss, Simon W. (1980). "The Integrals and Revisited". Journal of the Washington Academy of Sciences. 70 (4): 137–143. JSTOR 24537231.