Interstitial defect

The idea of interstitial compounds was started in the late 1930s and they are often called Hagg phases after Hägg.[1] Transition metals generally crystallise in either the hexagonal close packed or face centered cubic structures, both of which can be considered to be made up of layers of hexagonally close packed atoms. In both of these very similar lattices there are two sorts of interstice, or hole:

• Two tetrahedral holes per metal atom, i.e. the hole is between four metal atoms
• One octahedral hole per metal atom, i.e. the hole is between six metal atoms

It was suggested by early workers that:

• the metal lattice was relatively unaffected by the interstitial atom
• the electrical conductivity was comparable to that of the pure metal
• there was a range of composition
• the type of interstice occupied was determined by the size of the atom

These were not viewed as compounds, but rather as solutions, of say carbon, in the metal lattice, with a limiting upper “concentration” of the smaller atom that was determined by the number of interstices available.

A more detailed knowledge of the structures of metals, and binary and ternary phases of metals and non metals shows that:

• generally at low concentrations of the small atom, the phase can be described as a solution, and this approximates to the historical description of an interstitial compound above.
• at higher concentrations of the small atom, phases with different lattice structures may be present, and these may have a range of stoichiometries.

One example is the solubility of carbon in iron. The form of pure iron stable between 910 °C and 1390 °C, γ-iron, forms a solid solution with carbon termed austenite which is also known as steel.

Self-interstitial defects are interstitial defects which contain only atoms which are the same as those already present in the lattice.

Structure of self-interstitial in some common metals. The left-hand side of each crystal type shows the perfect crystal and the right-hand side the one with a defect.

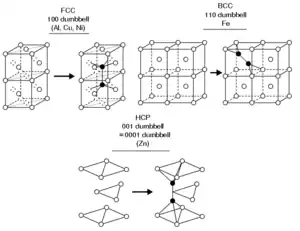
The structure of interstitial defects has been experimentally determined in some metals and semiconductors.

Contrary to what one might intuitively expect, most self-interstitials in metals with a known structure have a 'split' structure, in which two atoms share the same lattice site.[2][3] Typically the center of mass of the two atoms is at the lattice site, and they are displaced symmetrically from it along one of the principal lattice directions. For instance, in several common face-centered cubic (fcc) metals such as copper, nickel and platinum, the ground state structure of the self-interstitial is the split [100] interstitial structure, where two atoms are displaced in a positive and negative [100] direction from the lattice site. In body-centered cubic (bcc) iron the ground state interstitial structure is similarly a [110] split interstitial.

These split interstitials are often called dumbbell interstitials, because plotting the two atoms forming the interstitial with two large spheres and a thick line joining them makes the structure resemble a dumbbell weight-lifting device.

In other bcc metals than iron, the ground state structure is believed based on recent density-functional theory calculations to be the [111] crowdion interstitial,[4] which can be understood as a long chain (typically some 10–20) of atoms along the [111] lattice direction, compressed compared to the perfect lattice such that the chain contains one extra atom.

Structure of dumbbell self-interstitial in silicon. Note that the structure of the interstitial in silicon may depend on charge state and doping level of the material.

In semiconductors the situation is more complex, since defects may be charged and different charge states may have different structures. For instance, in silicon, the interstitial may either have a split [110] structure or a tetrahedral truly interstitial one.[5]

Carbon, notably in graphite and diamond, has a number of interesting self-interstitials - recently discovered using Local-density approximation-calculations is the "spiro-interestitial" in graphite, named after spiropentane, as the interstitial carbon atom is situated between two basal planes and bonded in a geometry similar to spiropentane.[6]

Small impurity interstitial atoms are usually on true interstitial sites between the lattice atoms. Large impurity interstitials can also be in split interstitial configurations together with a lattice atom, similar to those of the self-interstitial atom.

Interstitials modify the physical and chemical properties of materials.

• Interstitial carbon atoms have a crucial role for the properties and processing of steels, in particular carbon steels.
• Impurity interstitials can be used e.g. for storage of hydrogen in metals.
• The crystal lattice can expand with the concentration of impurity interstitials
• The amorphization of semiconductors such as silicon during ion irradiation is often explained by the build up of a high concentration of interstitials leading eventually to the collapse of the lattice as it becomes unstable.[7][8]
• Creation of large amounts of interstitials in a solid can lead to a significant energy buildup, which on release can even lead to severe accidents in certain old types of nuclear reactors (Wigner effect). The high-energy states can be released by annealing.
• At least in fcc lattice, interstitials have a large diaelastic softening effect on the material.[9]
• It has been proposed that interstitials are related to the onset of melting and the glass transition.[10][11][12]