Lemniscate constant

Gauss's constant ${\displaystyle G}$ is named after Carl Friedrich Gauss, who calculated it via the arithmetic–geometric mean as ${\displaystyle 1/M(1,{\sqrt {2}})}$.[6] By 1799, Gauss had two proofs of the theorem that ${\displaystyle M(1,{\sqrt {2}})=\pi /\varpi }$ where ${\displaystyle \varpi }$ is the lemniscate constant.[2][lower-alpha 1]

The lemniscate constant ${\displaystyle \varpi }$ and first lemniscate constant ${\displaystyle A}$ were proven transcendental by Theodor Schneider in 1937 and the second lemniscate constant ${\displaystyle B}$ and Gauss's constant ${\displaystyle G}$ were proven transcendental by Theodor Schneider in 1941.[11][17][lower-alpha 2] In 1975, Gregory Chudnovsky proved that the set ${\displaystyle \{\pi ,\varpi \}}$ is algebraically independent over ${\displaystyle \mathbb {Q} }$, which implies that ${\displaystyle A}$ and ${\displaystyle B}$ are algebraically independent as well.[18][19] But the set ${\displaystyle \{\pi ,M(1,1/{\sqrt {2}}),M'(1,1/{\sqrt {2}})\}}$ (where the prime denotes the derivative with respect to the second variable) is not algebraically independent over ${\displaystyle \mathbb {Q} }$. In fact,[20]

$${\displaystyle \pi =2{\sqrt {2}}{\frac {M^{3}(1,1/{\sqrt {2}})}{M'(1,1/{\sqrt {2}})}}={\frac {1}{G^{3}M'(1,1/{\sqrt {2}})}}.}$$

Usually, ${\displaystyle \varpi }$ is defined by the first equality below.[2][21][22]

$${\displaystyle {\begin{aligned}\varpi &=2\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}={\sqrt {2}}\int _{0}^{\infty }{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}=\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {t-t^{3}}}}=\int _{1}^{\infty }{\frac {\mathrm {d} t}{\sqrt {t^{3}-t}}}\\[6mu]&=4\int _{0}^{\infty }{\Bigl (}{\sqrt[{4}]{1+t^{4}}}-t{\Bigr )}\,\mathrm {d} t=2{\sqrt {2}}\int _{0}^{1}{\sqrt[{4}]{1-t^{4}}}\mathop {\mathrm {d} t} =3\int _{0}^{1}{\sqrt {1-t^{4}}}\,\mathrm {d} t\\[2mu]&=2K(i)={\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}={\frac {\Gamma (1/4)^{2}}{2{\sqrt {2\pi }}}}={\frac {2-{\sqrt {2}}}{4}}{\frac {\zeta (3/4)^{2}}{\zeta (1/4)^{2}}}\\[5mu]&=2.62205\;75542\;92119\;81046\;48395\;89891\;11941\ldots ,\end{aligned}}}$$

where K is the complete elliptic integral of the first kind with modulus k, Β is the beta function, Γ is the gamma function and ζ is the Riemann zeta function.

The lemniscate constant can also be computed by the arithmetic–geometric mean ${\displaystyle M}$,

$${\displaystyle \varpi ={\frac {\pi }{M(1,{\sqrt {2}})}}.}$$

Moreover,

$${\displaystyle e^{\beta '(0)}={\frac {\varpi }{\sqrt {\pi }}}}$$

which is analogous to

$${\displaystyle e^{\zeta '(0)}={\frac {1}{\sqrt {2\pi }}}}$$

where ${\displaystyle \beta }$ is the Dirichlet beta function and ${\displaystyle \zeta }$ is the Riemann zeta function.[23]

Gauss's constant is typically defined as the reciprocal of the arithmetic–geometric mean of 1 and the square root of 2, after his calculation of ${\displaystyle M(1,{\sqrt {2}})}$ published in 1800:[24]

$${\displaystyle G={\frac {1}{M(1,{\sqrt {2}})}}}$$

Gauss's constant is equal to

$${\displaystyle G={\frac {1}{2\pi }}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}}$$

where Β denotes the beta function. A formula for G in terms of Jacobi theta functions is given by

$${\displaystyle G=\vartheta _{01}^{2}\left(e^{-\pi }\right)}$$

Gauss's constant may be computed from the gamma function at argument 1/4:

$${\displaystyle G={\frac {\Gamma {\bigl (}{\tfrac {1}{4}}{\bigr )}{}^{2}}{2{\sqrt {2\pi ^{3}}}}}}$$

John Todd's lemniscate constants may be given in terms of the beta function B:

$${\displaystyle {\begin{aligned}A&={\tfrac {1}{2}}\pi G={\tfrac {1}{2}}\varpi ={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )},\\[3mu]B&={\frac {1}{2G}}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{2}},{\tfrac {3}{4}}{\bigr )}.\end{aligned}}}$$

Viète's formula for π can be written:

$${\displaystyle {\frac {2}{\pi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}}}\cdots }$$

An analogous formula for ϖ is:[25]

$${\displaystyle {\frac {2}{\varpi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\Bigg /}\!{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}}}\cdots }$$

The Wallis product for π is:

$${\displaystyle {\frac {\pi }{2}}=\prod _{n=1}^{\infty }\left(1+{\frac {1}{n}}\right)^{(-1)^{n+1}}=\prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right)={\biggl (}{\frac {2}{1}}\cdot {\frac {2}{3}}{\biggr )}{\biggl (}{\frac {4}{3}}\cdot {\frac {4}{5}}{\biggr )}{\biggl (}{\frac {6}{5}}\cdot {\frac {6}{7}}{\biggr )}\cdots }$$

An analogous formula for ϖ is:[26]

$${\displaystyle {\frac {\varpi }{2}}=\prod _{n=1}^{\infty }\left(1+{\frac {1}{2n}}\right)^{(-1)^{n+1}}=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n-2}}\cdot {\frac {4n}{4n+1}}\right)={\biggl (}{\frac {3}{2}}\cdot {\frac {4}{5}}{\biggr )}{\biggl (}{\frac {7}{6}}\cdot {\frac {8}{9}}{\biggr )}{\biggl (}{\frac {11}{10}}\cdot {\frac {12}{13}}{\biggr )}\cdots }$$

A related result for Gauss's constant (${\displaystyle G=\varpi /\pi }$) is:[27]

$${\displaystyle G=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n}}\cdot {\frac {4n+2}{4n+1}}\right)={\biggl (}{\frac {3}{4}}\cdot {\frac {6}{5}}{\biggr )}{\biggl (}{\frac {7}{8}}\cdot {\frac {10}{9}}{\biggr )}{\biggl (}{\frac {11}{12}}\cdot {\frac {14}{13}}{\biggr )}\cdots }$$

An infinite series of Gauss's constant discovered by Gauss is:[28]

$${\displaystyle G=\sum _{n=0}^{\infty }(-1)^{n}\prod _{k=1}^{n}{\frac {(2k-1)^{2}}{(2k)^{2}}}=1-{\frac {1^{2}}{2^{2}}}+{\frac {1^{2}\cdot 3^{2}}{2^{2}\cdot 4^{2}}}-{\frac {1^{2}\cdot 3^{2}\cdot 5^{2}}{2^{2}\cdot 4^{2}\cdot 6^{2}}}+\cdots }$$

The Machin formula for π is ${\textstyle {\tfrac {1}{4}}\pi =4\arctan {\tfrac {1}{5}}-\arctan {\tfrac {1}{239}},}$ and several similar formulas for π can be developed using trigonometric angle sum identities, e.g. Euler's formula ${\textstyle {\tfrac {1}{4}}\pi =\arctan {\tfrac {1}{2}}+\arctan {\tfrac {1}{3}}}$. Analogous formulas can be developed for ϖ, including the following found by Gauss: ${\displaystyle {\tfrac {1}{2}}\varpi =2\operatorname {arcsl} {\tfrac {1}{2}}+\operatorname {arcsl} {\tfrac {7}{23}}}$, where ${\displaystyle \operatorname {arcsl} }$ is the lemniscate arcsine.[29]

The lemniscate constant can be rapidly computed by the series[30][31]

${\displaystyle \varpi =2^{-1/2}\pi \left(\sum _{n\in \mathbb {Z} }e^{-\pi n^{2}}\right)^{2}=2^{1/4}\pi e^{-\pi /12}\left(\sum _{n\in \mathbb {Z} }(-1)^{n}e^{-\pi p_{n}}\right)^{2}}$

where ${\displaystyle p_{n}=(3n^{2}-n)/2}$ (these are the generalized pentagonal numbers).

In a spirit similar to that of the Basel problem,

${\displaystyle \sum _{z\in \mathbb {Z} [i]\setminus \{0\}}{\frac {1}{z^{4}}}=G_{4}(i)={\frac {\varpi ^{4}}{15}}}$

where ${\displaystyle \mathbb {Z} [i]}$ are the Gaussian integers and ${\displaystyle G_{4}}$ is the Eisenstein series of weight ${\displaystyle 4}$ (see Lemniscate elliptic functions § Hurwitz numbers for a more general result).[32]

A related result is

${\displaystyle \sum _{n=1}^{\infty }\sigma _{3}(n)e^{-2\pi n}={\frac {\varpi ^{4}}{80\pi ^{4}}}-{\frac {1}{240}}}$

where ${\displaystyle \sigma _{3}}$ is the sum of positive divisors function.[33]

In 1842, Malmsten found

${\displaystyle \sum _{n=1}^{\infty }(-1)^{n+1}{\frac {\log(2n+1)}{2n+1}}={\frac {\pi }{4}}\left(\gamma +2\log {\frac {\pi }{\varpi {\sqrt {2}}}}\right)}$

where ${\displaystyle \gamma }$ is Euler's constant.

Gauss's constant is given by the rapidly converging series

$${\displaystyle G={\sqrt[{4}]{32}}e^{-{\frac {\pi }{3}}}\left(\sum _{n=-\infty }^{\infty }(-1)^{n}e^{-2n\pi (3n+1)}\right)^{2}.}$$

The constant is also given by the infinite product

${\displaystyle G=\prod _{m=1}^{\infty }\tanh ^{2}\left({\frac {\pi m}{2}}\right).}$

A (generalized) continued fraction for π is

$${\displaystyle {\frac {\pi }{2}}=1+{\cfrac {1}{1+{\cfrac {1\cdot 2}{1+{\cfrac {2\cdot 3}{1+{\cfrac {3\cdot 4}{1+\ddots }}}}}}}}}$$

An analogous formula for ϖ is[12]

$${\displaystyle {\frac {\varpi }{2}}=1+{\cfrac {1}{2+{\cfrac {2\cdot 3}{2+{\cfrac {4\cdot 5}{2+{\cfrac {6\cdot 7}{2+\ddots }}}}}}}}}$$

Define Brouncker's continued fraction by[34]

$${\displaystyle b(s)=s+{\cfrac {1^{2}}{2s+{\cfrac {3^{2}}{2s+{\cfrac {5^{2}}{2s+\ddots }}}}}},\quad s>0.}$$

Let ${\displaystyle n\geq 0}$ except for the first equality where ${\displaystyle n\geq 1}$. Then[35][36]

$${\displaystyle {\begin{aligned}b(4n)&=(4n+1)\prod _{k=1}^{n}{\frac {(4k-1)^{2}}{(4k-3)(4k+1)}}{\frac {\pi }{\varpi ^{2}}}\\b(4n+1)&=(2n+1)\prod _{k=1}^{n}{\frac {(2k)^{2}}{(2k-1)(2k+1)}}{\frac {4}{\pi }}\\b(4n+2)&=(4n+1)\prod _{k=1}^{n}{\frac {(4k-3)(4k+1)}{(4k-1)^{2}}}{\frac {\varpi ^{2}}{\pi }}\\b(4n+3)&=(2n+1)\prod _{k=1}^{n}{\frac {(2k-1)(2k+1)}{(2k)^{2}}}\,\pi .\end{aligned}}}$$

For example,

$${\displaystyle {\begin{aligned}b(1)&={\frac {4}{\pi }}\\b(2)&={\frac {\varpi ^{2}}{\pi }}\\b(3)&=\pi \\b(4)&={\frac {9\pi }{\varpi ^{2}}}.\end{aligned}}}$$

Simple continued fractions[37][38]

$${\displaystyle {\begin{aligned}\varpi &=[2,1,1,1,1,1,4,1,2,\ldots ]\\2\varpi &=[5,4,10,2,1,2,3,29,\ldots ]\\{\frac {\varpi }{2}}&=[1,3,4,1,1,1,5,2,\ldots ]\\G&=[0,1,5,21,3,4,14,\ldots ]\end{aligned}}}$$

A geometric representation of ${\displaystyle \varpi /2}$ and ${\displaystyle \varpi /{\sqrt {2}}}$

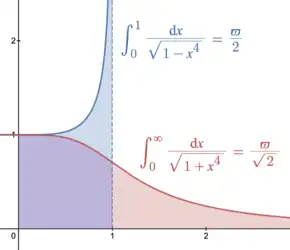
ϖ is related to the area under the curve ${\displaystyle x^{4}+y^{4}=1}$. Defining ${\displaystyle \pi _{n}\mathrel {:=} \mathrm {B} {\bigl (}{\tfrac {1}{n}},{\tfrac {1}{n}}{\bigr )}}$, twice the area in the positive quadrant under the curve ${\displaystyle x^{n}+y^{n}=1}$ is ${\textstyle 2\int _{0}^{1}{\sqrt[{n}]{1-x^{n}}}\mathop {\mathrm {d} x} ={\tfrac {1}{n}}\pi _{n}.}$ In the quartic case, ${\displaystyle {\tfrac {1}{4}}\pi _{4}={\tfrac {1}{\sqrt {2}}}\varpi .}$

In 1842, Malmsten discovered that[39]

$${\displaystyle \int _{0}^{1}{\frac {\log(-\log x)}{1+x^{2}}}\,dx={\frac {\pi }{2}}\log {\frac {\pi }{\varpi {\sqrt {2}}}}.}$$

Furthermore,

$${\displaystyle \int _{0}^{\infty }{\frac {\tanh x}{x}}e^{-x}\,dx=\log {\frac {\varpi ^{2}}{\pi }}}$$

and[40]

$${\displaystyle \int _{0}^{\infty }e^{-x^{4}}\,dx={\frac {\sqrt {2\varpi {\sqrt {2\pi }}}}{4}},\quad {\text{analogous to}}\,\int _{0}^{\infty }e^{-x^{2}}\,dx={\frac {\sqrt {\pi }}{2}},}$$

a form of Gaussian integral.

Gauss's constant appears in the evaluation of the integrals

$${\displaystyle {\frac {1}{G}}=\int _{0}^{\frac {\pi }{2}}{\sqrt {\sin(x)}}\,dx=\int _{0}^{\frac {\pi }{2}}{\sqrt {\cos(x)}}\,dx}$$

$${\displaystyle G=\int _{0}^{\infty }{\frac {dx}{\sqrt {\cosh(\pi x)}}}}$$

The first and second lemniscate constants are defined by integrals:[11]

$${\displaystyle A=\int _{0}^{1}{\frac {dx}{\sqrt {1-x^{4}}}}}$$

$${\displaystyle B=\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}$$

Circumference of an ellipse

Gauss's constant satisfies the equation[41]

$${\displaystyle {\frac {1}{G}}=2\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}$$

Euler discovered in 1738 that for the rectangular elastica (first and second lemniscate constants)[42][41]

$${\displaystyle {\textrm {arc}}\ {\textrm {length}}\cdot {\textrm {height}}=A\cdot B=\int _{0}^{1}{\frac {\mathrm {d} x}{\sqrt {1-x^{4}}}}\cdot \int _{0}^{1}{\frac {x^{2}\mathop {\mathrm {d} x} }{\sqrt {1-x^{4}}}}={\frac {\varpi }{2}}\cdot {\frac {\pi }{2\varpi }}={\frac {\pi }{4}}}$$

Now considering the circumference ${\displaystyle C}$ of the ellipse with axes ${\displaystyle {\sqrt {2}}}$ and ${\displaystyle 1}$, satisfying ${\displaystyle 2x^{2}+4y^{2}=1}$, Stirling noted that[43]

$${\displaystyle {\frac {C}{2}}=\int _{0}^{1}{\frac {dx}{\sqrt {1-x^{4}}}}+\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}$$

Hence the full circumference is

$${\displaystyle C={\frac {1}{G}}+G\pi \approx 3.820197789\ldots }$$

This is also the arc length of the sine curve on half a period:[44]

$${\displaystyle C=\int _{0}^{\pi }{\sqrt {1+\cos ^{2}(x)}}\,dx}$$

• Weisstein, Eric W. "Gauss's Constant". MathWorld.
• Sequences A014549, A053002, and A062539 in OEIS
• Cox, David A. (January 1984). "The Arithmetic-Geometric Mean of Gauss" (PDF). L'Enseignement Mathématique. 30 (2): 275–330. doi:10.5169/seals-53831. Retrieved 25 June 2022.

• "Gauss's constant and where it occurs". www.johndcook.com. 2021-10-17.