Looming and similar refraction phenomena

While mirages are the best known atmospheric refraction phenomena, looming and similar refraction phenomena do not produce mirages. Mirages show an extra image or images of the miraged object, while looming, towering, stooping, and sinking do not. No inverted image is present in those phenomena either. Depending on atmospheric conditions, the objects can appear to be elevated or lowered, stretched or stooped. These phenomena can occur together, changing the appearance of different parts of the objects in different ways. Sometimes these phenomena can occur together with a true mirage.[1][2]

The distant boats appear to be floating in the sky as a result of looming and other refraction phenomena.

Looming
Looming of the Canadian coast as seen from Rochester, New York, on April 16, 1871

Looming is the most noticeable and most often observed of these refraction phenomena. It is an abnormally large refraction of the object that increases the apparent elevation of the distant objects and sometimes allows an observer to see objects that are located below the horizon under normal conditions. One of the most famous looming observations was made by William Latham in 1798, who wrote:

I could very plainly see the cliffs on the opposite coast; which, at the nearest part, are between forty and fifty miles distant, and are not to be discerned, from that low situation, by the aid of the best glasses. They appeared to be only a few miles off, and seemed to extend for some leagues along the coast.[3]

Thomas Jefferson noted the phenomenon of looming in his book Notes on the State of Virginia:

There is a solitary mountain about 40 miles off, in the South, whose natural shape as presented to view there, is a regular cone; but, by the effect of looming it sometimes subsides almost totally into the horizon; sometimes it rises more acute and more elevated, its top flat, and as broad as its base. In short it assumes at times the most whimsical shapes, and all these perhaps successively in the same morning.[4]

He was unable to explain this phenomenon and did not think refraction could account from the perceived changes of shape of the object in question.

Other famous observations that were called "mirages" may actually be referring to looming. One of those was described in Scientific American on August 25, 1894, as "a remarkable mirage seen by the citizens of Buffalo, New York".[5][6][7] Such looming—sometimes with apparent magnification of opposite shores—have been reported over the Great Lakes. Canadian shorelines have been observed from Rochester, New York, across Lake Ontario, and from Cleveland across Lake Erie. The landforms over 50 miles (80 km) distant, normally beyond the horizon, were sometimes perceived as 6 miles (10 km) away.

Looming is most commonly seen in the polar regions. Looming was sometimes responsible for the errors made by polar explorers; for example, Charles Wilkes charted the coast of Antarctica, where later only water was found.

The larger the size of the sphere (the planet where an observer is located) the less curved the horizon is. William Jackson Humphreys' calculations showed that an observer may be able to see all the way around a planet of sufficient size and with sufficient atmospheric density gradient.[8]

Sinking

Sinking is the opposite of looming. In sinking, stationary objects that are normally seen above the horizon appear to be lowered, or may even disappear below the horizon. In looming, the curvature of the rays is increasing, while sinking produces the opposite effect.[9] In general, looming is more noticeable than sinking because objects that appear to grow stand out more than those that appear to shrink.

Towering and stooping

Towering and stooping are more complex forms of atmospheric refraction than looming and sinking. While looming and sinking change the apparent elevation of an object, towering and stooping change the apparent shape of the object itself. With towering, objects appear stretched; with stooping, objects seem to be shortened. The apparent stretching and shortening of the objects are not symmetrical and depends on the thermal profile of the atmosphere. The curvature of the rays changes more rapidly in some places because the thermal profile is curved.[2][9]

Image example and explanation
Three photos showing a looming, towering, and Fata Morgana of the Farallon Islands

These three images were taken from the same place on different days under different atmospheric conditions. The top frame shows looming. The island shape is not distorted, but is elevated. The middle frame shows looming with towering. The lowest frame is a 5-image superior mirage of the islands. As the image shows, the different refraction phenomena are not independent from each other and may occur together as a combination, depending on atmospheric conditions.[2]

See also

References
  1. Heidorn, Keith (July 15, 1999). "The Superior Mirage: Seeing Beyond". The Weather Doctor. Retrieved April 23, 2010.
  2. Young, Andrew. "Looming, Towering, Stooping, and Sinking". San Diego State University. Retrieved April 23, 2010.
  3. Latham, William (1798). "Account of a Singular Instance of Atmospherical Refraction". Philosophical Transactions. 88: 357–360. JSTOR 106981.
  4. Jefferson, Thomas (1955). Notes on the State of Virginia. Chapel Hill, Published for the Institute of Early American History and Culture, Williamsburg, Va., by the University of North Carolina Press.
  5. "A mirage at Buffalo". Scientific American. 71: 115. August 25, 1894 – via Google Books. open access
  6. Miscellaneous notes and queries. Vol. 12. Manchester, New Hampshire: S. C. and L. M. Gould. 1894. p. 314. OCLC 448141550.
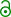
  7. "Mirage seen: Toronto Bay and City brought close to Buffalo". The Buffalo Commercial. August 16, 1894. p. 9. Retrieved July 1, 2018 – via Newspapers.com. icon of an open green padlock
  8. Humphreys, William Jackson (1920). Physics of the Air. Philadelphia: Pub. for the Franklin Institute of the State of Pennsylvania by J.B. Lippincott company. pp. 447–448.
    If, now, the density of the air at the place in question decreases with increase of elevation, as it nearly always does, the upper portion of the wave front will travel faster than the lower, and the path will be bent down towards the earth along a curve whose radius depends upon the rate of this density decrease. For example, let the corrected height of the barometer be 760 mm., the temperature 17 °C., and the rate of temperature decrease with elevation 5 °C. per kilometre; conditions that not infrequently obtain at sea level. On substituting these values in the density elevation equation, it appears that the density gradient would be such that if continuous the limit of the atmosphere would be reached at an elevation of about 10 kilometres. Hence, under these circumstances, the velocity of light at an elevation of 10 kilometres would be to its velocity at the surface in the ratio of 1,000,276 to 1,000,000, approximately, since the refractive index of the lower air would be 1.000,276, about. The radius of curvature, r, therefore, is closely given in kilometres by the equation, Hence, r = 36,232 kilometres, or approximately 5.7 times the radius of the earth. It is conceivable, therefore, that the size of a planet and the vertical density gradient of its atmosphere might be such that one's horizon on it would include the entire surface—that he could look all the way round and, as some one has said, see his own back.
  9. Humphreys, William Jackson (1920). Physics of the air. J. B. Lippincott Company. p. 449. OCLC 569637. looming.
Wikimedia Commons has media related to Mirage.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.