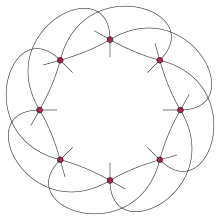
Möbius–Kantor configuration

August Ferdinand Möbius (1828) asked whether there exists a pair of polygons with p sides each, having the property that the vertices of one polygon lie on the lines through the edges of the other polygon, and vice versa. If so, the vertices and edges of these polygons would form a projective configuration. For ${\displaystyle p=4}$ there is no solution in the Euclidean plane, but Seligmann Kantor (1882) found pairs of polygons of this type, for a generalization of the problem in which the points and edges belong to the complex projective plane. That is, in Kantor's solution, the coordinates of the polygon vertices are complex numbers. Kantor's solution for ${\displaystyle p=4}$, a pair of mutually-inscribed quadrilaterals in the complex projective plane, is called the Möbius–Kantor configuration.

Seven of the lines of the configuration can be made straight, but not all eight

H. S. M. Coxeter (1950) supplies the following simple complex projective coordinates for the eight points of the Möbius–Kantor configuration:

(1,0,0), (0,0,1), (ω, −1, 1), (−1, 0, 1),

(−1,ω²,1), (1,ω,0), (0,1,0), (0,−1,1),

where ω denotes a complex cube root of 1.

The eight points and eight lines of the Möbius–Kantor configuration, with these coordinates, form the eight vertices and eight 3-edges of the complex polygon 3{3}3.[1] Coxeter named it a Möbius–Kantor polygon.

The Möbius–Kantor graph, the Levi graph of the Möbius–Kantor configuration. Vertices of one color represent the points of the configuration, and vertices of the other color represent the lines.

More abstractly, the Möbius–Kantor configuration can be described as a system of eight points and eight triples of points such that each point belongs to exactly three of the triples. With the additional conditions (natural to points and lines) that no pair of points belong to more than one triple and that no two triples have more than one point in their intersection, any two systems of this type are equivalent under some permutation of the points. That is, the Möbius–Kantor configuration is the unique projective configuration of type (8₃8₃).

The Möbius–Kantor graph derives its name from being the Levi graph of the Möbius–Kantor configuration. It has one vertex per point and one vertex per triple, with an edge connecting two vertices if they correspond to a point and to a triple that contains that point.

The points and lines of the Möbius–Kantor configuration can be described as a matroid, whose elements are the points of the configuration and whose nontrivial flats are the lines of the configuration. In this matroid, a set S of points is independent if and only if either ${\displaystyle |S|\leq 2}$ or S consists of three non-collinear points. As a matroid, it has been called the MacLane matroid, after the work of Saunders MacLane (1936) proving that it cannot be oriented; it is one of several known minor-minimal non-orientable matroids.[2]

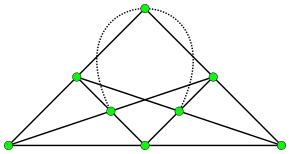
The solution to Möbius' problem of mutually inscribed polygons for values of p greater than four is also of interest. In particular, one possible solution for ${\displaystyle p=5}$ is the Desargues configuration, a set of ten points and ten lines, three points per line and three lines per point, that does admit a Euclidean realization. The Möbius configuration is a three-dimensional analogue of the Möbius–Kantor configuration consisting of two mutually inscribed tetrahedra.

The Möbius–Kantor configuration can be augmented by adding four lines through the four pairs of points not already connected by lines, and by adding a ninth point on the four new lines. The resulting configuration, the Hesse configuration, shares with the Möbius–Kantor configuration the property of being realizable with complex coordinates but not with real coordinates.[3] Deleting any one point from the Hesse configuration produces a copy of the Möbius–Kantor configuration. Both configurations may also be described algebraically in terms of the abelian group ${\displaystyle \mathbb {Z} _{3}\times \mathbb {Z} _{3}}$ with nine elements. This group has four subgroups of order three (the subsets of elements of the form ${\displaystyle (i,0)}$, ${\displaystyle (i,i)}$, ${\displaystyle (i,2i)}$, and ${\displaystyle (0,i)}$ respectively), each of which can be used to partition the nine group elements into three cosets of three elements per coset. These nine elements and twelve cosets form the Hesse configuration. Removing the zero element and the four cosets containing zero gives rise to the Möbius–Kantor configuration.

• Coxeter, H. S. M. (1950), "Self-dual configurations and regular graphs", Bulletin of the American Mathematical Society, 56 (5): 413–455, doi:10.1090/S0002-9904-1950-09407-5, MR 0038078.
• Coxeter, H. S. M.; Shephard, G. C. (1992), "Portraits of a family of complex polytopes", Leonardo, 25 (3/4): 239, doi:10.2307/1575843, JSTOR 1575843. Reprinted in The Visual Mind, MIT Press, 1993, pp. 19–26, MR1255836.
• Dolgachev, Igor V. (2004), "Abstract configurations in algebraic geometry", The Fano Conference, Turin: University of Torino, pp. 423–462, arXiv:math.AG/0304258, MR 2112585.
• Kantor, Seligmann (1882), "Über die Configurationen (3, 3) mit den Indices 8, 9 und ihren Zusammenhang mit den Curven dritter Ordnung", Sitzungsberichte der Mathematisch-Naturwissenschaftlichen Classe der Kaiserlichen Akademie der Wissenschaften, Wien, 84 (1): 915–932.
• MacLane, Saunders (1936), "Some Interpretations of Abstract Linear Dependence in Terms of Projective Geometry", American Journal of Mathematics, 58 (1): 236–240, doi:10.2307/2371070, MR 1507146.
• Möbius, August Ferdinand (1828), "Kann von zwei dreiseitigen Pyramiden eine jede in Bezug auf die andere um- und eingeschrieben zugleich heissen?" (PDF), Journal für die reine und angewandte Mathematik, 3: 273–278. In Gesammelte Werke (1886), vol. 1, pp. 439–446.
• Ziegler, Günter M. (1991), "Some minimal non-orientable matroids of rank three", Geometriae Dedicata, 38 (3): 365–371, doi:10.1007/BF00181199, MR 1112674.

• Weisstein, Eric W., "Möbius-Kantor Configuration", MathWorld