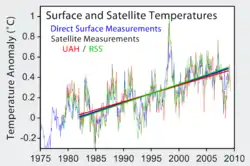
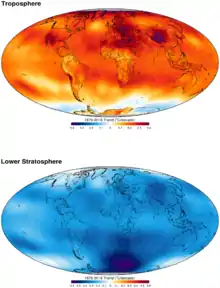
Microwave Sounding Unit temperature measurements
Microwave Sounding Unit temperature measurements refers to temperature measurement using the Microwave Sounding Unit instrument and is one of several methods of measuring Earth atmospheric temperature from satellites. Microwave measurements have been obtained from the troposphere since 1979, when they were included within NOAA weather satellites, starting with TIROS-N. By comparison, the usable balloon (radiosonde) record begins in 1958 but has less geographic coverage and is less uniform.
Microwave brightness measurements do not directly measure temperature. They measure radiances in various wavelength bands, which must then be mathematically inverted to obtain indirect inferences of temperature.[1][2] The resulting temperature profiles depend on details of the methods that are used to obtain temperatures from radiances. As a result, different groups that have analyzed the satellite data have obtained different temperature trends. Among these groups are Remote Sensing Systems (RSS) and the University of Alabama in Huntsville (UAH). The satellite series is not fully homogeneous – the record is constructed from a series of satellites with similar but not identical instrumentation. The sensors deteriorate over time, and corrections are necessary for satellite drift in orbit. Particularly large differences between reconstructed temperature series occur at the few times when there is little temporal overlap between successive satellites, making intercalibration difficult.
Creation of the satellite temperature record
From 1979 to 2005 the microwave sounding units (MSUs) and since 1998 the Advanced Microwave Sounding Units on NOAA polar orbiting satellites have measured the intensity of upwelling microwave radiation from atmospheric oxygen. The intensity is proportional to the temperature of broad vertical layers of the atmosphere, as demonstrated by theory and direct comparisons with atmospheric temperatures from radiosonde (balloon) profiles.
Different frequencies sample a different weighted range of the atmosphere, depending on the absorption depth (i.e., optical depth) of the microwaves through the atmosphere.[3][4] To derive data of the temperature profile at lower altitudes and remove the stratospheric influence, researchers have developed synthetic products by subtracting signals at different altitude and view angles; such as "2LT", which has a maximum at about 650 hPa. However this process amplifies noise,[5] increases inter-satellite calibration biases and enhances surface contamination.[6]
Records have been created by merging data from nine different MSUs and AMSU data, each with peculiarities that must be calculated and removed because they can have substantial impacts on the resulting trend.[7] The process of constructing a temperature record from a radiance record is difficult and some of the required corrections are as large as the trend itself: [8]
Analysis technique
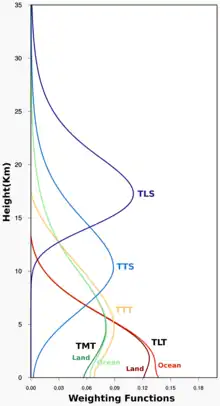
Upwelling radiance is measured at different frequencies; these different frequency bands sample a different weighted range of the atmosphere.[3] Since the atmosphere is partially but not completely opaque, the brightness measured is an average across a band of atmosphere, depending on the penetration depth of the microwaves.[4] The brightness temperature (TB) measured by satellite is given by:[9]
where is the surface weight, and are the temperatures at the surface and at the atmospheric level and is the atmospheric weighting function.
Both the surface and atmospheric weights are dependent on the surface emissivity , the absorption coefficient and the earth incidence angle ; the surface weight is the product of and an attenuation factor:
where the secant theta term accounts for the dependence of optical path length on the vertical angle, and is the optical depth:
The atmospheric weighting functions can be written as:
The first term in this equation is related to the radiation emitted upward from the level and attenuated along the path to the top of the atmosphere (∞), the second include the radiation emitted downward from the level z to the surface (0) and the radiation reflected back by the surface (proportional to ) to the top of the atmosphere, the exact form of is dependent upon the temperature, water vapor and liquid water content of the atmosphere.
Channels
MSU Channel 1 is not used to monitor atmospheric temperature because it's too much sensitive to the emission from the surface, furthermore it is heavily contaminated by water vapor/liquid water in the lowermost troposphere.[10]
Channel 2 or TMT is broadly representative of the troposphere, albeit with a significant overlap with the lower stratosphere; the weighting function has its maximum at 350 hPa (corresponding to about 8 km altitude)[11] and half-power at about 40 and 800 hPa (roughly 2–22 km).
Figure 3 (right) shows the atmospheric levels sampled by different wavelength from the satellite measurements, where TLS, TTS, and TTT represent three different wavelengths. Note that the lowest measurement, TTT, includes brightness from both atmospheric and surface emission. TMT and TLT represent the altitude range computed lower troposphere temperature calculated using an atmospheric model as discussed below.
The T4 or TLS channel in representative of the temperature in the lower stratosphere with a peak weighting function at around 17 km above the earth surface.
- Calculation of lower troposphere temperature
In an attempt to derive data for lower altitudes and remove the stratospheric influence, several researchers have developed synthetic products that subtract the higher-altitude values from the lowest altitude (TMT) measurement. Such a data-analysis technique is dependent on modeling the effect of altitude on temperature. However, this process amplifies noise,[5] increases inter-satellite calibration biases and enhances surface contamination.[6] Spencer and Christy developed the synthetic "2LT" (later renamed "TLT") product by subtracting signals at different view angles; this has a maximum at about 650 hPa. The 2LT product has gone through numerous versions as various corrections have been applied. Another such methodology has been developed by Fu and Johanson,[12] the TTT(Total Troposphere Temperature) channel is a linear combination of the TMT and TLS channel: TTT=1.156*TMT-0.153*TLS for the global average and TTT=1.12*TMT-0.11*TLS at tropical latitudes
Measurement corrections
- Diurnal sampling
All the MSU instruments and to a lesser extent AMSU drift slowly from the sun-synchronous equatorial crossing time changing the local time observed by the instrument, therefore the natural diurnal cycle may be aliased into the long term trend. The diurnal sampling correction is in the order of a few hundredths °C/decade for TLT and TMT.
- Orbit decay
All Polar orbiting satellite lose height after launch, the orbital decay is stronger during period of elevated solar activity when the enhanced ultraviolet radiation warm the upper atmosphere and increase the frictional drag over the spacecraft.
The orbital decay change the instrument view angle relative to the surface and thus the observed microwave emissivity, furthermore the long term time-series is constructed by sequential merging of the inter-calibrated satellite data so that the error is summed up over time, the required correction is in the order of 0.1 °C/decade for TLT.
- Calibration changes
Once every earth scan MSU instrument use the deep space (2.7K) and on-board warm targets to make calibration measures, however as the spacecraft drifts through the diurnal cycle the calibration target temperature may change due to varying solar shadowing effect, the correction is in the order of 0.1 °C/decade for TLT and TMT.
One widely reported satellite temperature record is that developed by Roy Spencer and John Christy at the University of Alabama in Huntsville (UAH). The record comes from a succession of different satellites and problems with inter-calibration between the satellites are important, especially NOAA-9, which accounts for most of the difference between the RSS and UAH analyses.[13] NOAA-11 played a significant role in a 2005 study by Mears et al. identifying an error in the diurnal correction that leads to the 40% jump in Spencer and Christy's trend from version 5.1 to 5.2.[14]
Trends
Records have been created by merging data from nine different MSUs, each with peculiarities (e.g., time drift of the spacecraft relative to the local solar time) that must be calculated and removed because they can have substantial impacts on the resulting trend.[7]
The process of constructing a temperature record from a radiance record is difficult. The satellite temperature record comes from a succession of different satellites and problems with inter-calibration between the satellites are important, especially NOAA-9, which accounts for most of the difference between various analyses.[15] NOAA-11 played a significant role in a 2005 study by Mears et al. identifying an error in the diurnal correction that leads to the 40% jump in Spencer and Christy's trend from version 5.1 to 5.2.[14] There are ongoing efforts to resolve differences in satellite temperature datasets.
Comparison with surface trends
To compare the MSU retrievals to the trend from the surface temperature record it is most appropriate to derive trends for the part of the atmosphere nearest the surface, i.e., the lower troposphere. As discussed earlier, the lowest of the temperature retrievals, TLT, is not a direct measurement, but a value calculated by subtracting higher altitude brightness temperature from the lower measurements. The trends found from the UAH and the RSS groups, shown in the table below, are calculated by slightly different methods, and result in different values for the trends.
Using the T2 or TMT channel (which include significant contributions from the stratosphere, which has cooled), Mears et al. of Remote Sensing Systems (RSS) find (through January 2017) a trend of +0.140 °C/decade.[16] Spencer and Christy of the University of Alabama in Huntsville (UAH), find a smaller trend of +0.08 °C/decade.[17]
In comparing these measurements to surface temperature models, it is important to note that resulting values for the lower troposphere measurements taken by the MSU is a weighted average of temperatures over multiple altitudes (roughly 0 to 12 km), and not a surface temperature (see TLT in figure 3 above). The results are thus not precisely comparable to surface temperature models.
Trends from the record
| Channel | Start | End Date | RSS v4.0 | UAH v6.0
Global Trend |
STAR v3.0
Global Trend |
UW UAH
Global Trend |
UW RSS
Global Trend |
|---|---|---|---|---|---|---|---|
| TLT | 1979 | 2017-05 | 0.184 | 0.12[22] | |||
| TTT | 1979 | 2017-01 | 0.180 | 0.13 | 0.14 | ||
| TMT | 1979 | 2017-01 | 0.140 | 0.08[23] | 0.129 | ||
| TLS | 1979 | 2017-01 | −0.260 | −0.31[24] | −0.263 | ||
Another satellite temperature analysis is provided by NOAA/NESDIS STAR Center for Satellite Application and Research and use simultaneous nadir overpasses (SNO) [25] to remove satellite intercalibration biases yielding more accurate temperature trends. The STAR-NOAA analysis finds a 1979–2016 trend of +0.129 °C/decade for TMT channel.[20]
Using an alternative adjustment to remove the stratospheric contamination,[26] 1979–2011 trends of +0.14 °C/decade when applied to the RSS data set and +0.11 °C/decade when applied to the UAH data set were found.[27]
A University of Washington analysis finds 1979–2012 trends of +0.13 °C/decade when applied to the RSS data set and +0.10 °C/decade when applied to the UAH data set.[28]
Combined surface and satellite data
In 2013, Cowtan and Way suggested[29][30] that global temperature averages based on surface temperature data had a possible source of bias due to incomplete global coverage if the unsampled regions are not uniformly distributed over the planet's surface. They addressed this problem by combining the surface temperature measurements with satellite data to fill in the coverage. Over the time period 1979-2016, combining the HadCRUT4 surface data with UAH satellite coverage, they show a global surface-warming trend of 0.188 °C/decade.[31]
History of satellite temperature data interpretation
The early (1978 to early 2000s) disagreement between the surface temperature record and the satellite records was a subject of research and debate. A lack of warming then seen in the UAH retrieval trends 1978-1998 was noted by Christy and Spencer[32] and commented on in a 2000 report by the National Research Council[33][34] and the 2001 IPCC Third Assessment Report[35]
Christy et al. (2007) claimed that tropical temperature trends from radiosondes matches closest with his v5.2 UAH dataset.[36] Furthermore, they asserted there was a discrepancy between RSS and sonde trends beginning in 1992, when the NOAA-12 satellite was launched.[37]
In 1998 the UAH data had showed a cooling of 0.05K per decade (at 3.5 km – mid to low troposphere). Wentz & Schabel at RSS in their 1998 paper showed this (along with other discrepancies) was due to the orbital decay of the NOAA satellites.[38] Once the orbital changes had been allowed for the data showed a 0.07K per decade increase in temperature at this level of the atmosphere.
Another important critique of the early satellite record was its shortness—adding a few years on to the record or picking a particular time frame could change the trends considerably.
Through early 2005, even though they began with the same data, each of the major research groups had interpreted it with different results. Most notably, Mears et al. at RSS found 0.193 °C/decade for lower troposphere up to July 2005, compared to +0.123 °C/decade found by UAH for the same period.
There were ongoing efforts to resolve these differences. Much of the disparity in early results was resolved by the three papers in Science, 11 August 2005, which pointed out errors in the UAH 5.1 record and the radiosonde record in the tropics.
An alternative adjustment to remove the stratospheric contamination has been introduced by Fu et al. (2004).[26] After the correction the vertical weighting function is nearly the same of the T2(TMT) channel in the troposphere.[39]
Another re-analysis, by Vinnikov et al. in 2006, found +0.20 °C per decade (1978–2005).[40]
Analysis over a longer time period has resolved some, but not all, of the discrepancy in the data. The IPCC Fifth Assessment Report (2014) stated: "based on multiple independent analyses of measurements from radiosondes and satellite sensors it is virtually certain that globally the troposphere has warmed and the stratosphere has cooled since the mid-20th century. Despite unanimous agreement on the sign of the trends, substantial disagreement exists among available estimates as to the rate of temperature changes, particularly outside the NH extratropical troposphere, which has been well sampled by radiosondes,[41] and concluded "Although there have been substantial methodological debates about the calculation of trends and their uncertainty, a 95% confidence interval of around ±0.1 °C per decade has been obtained consistently for both LT and MT (e.g., Section 2.4.4; McKitrick et al., 2010).[42]
Corrections to UAH data trends
As well as the correction by Wentz and Schabel,[38] doubts had been raised as early as 2000 about the UAH analysis by the work of Prabhakara et al.,[43] which minimised errors due to satellite drift. They found a trend of 0.13 °C/decade, in reasonable agreement with surface trends.
Since the earliest releast of results in the 1990s, a number of adjustments to the algorithm computing the UAH TLT dataset have been made.[44][8] A table of the corrections can be found in the UAH satellite temperature dataset article.
Recent trend summary
To compare to the trend from the surface temperature record (+0.161±0.033 °C/decade from 1979 to 2012 according to NASA GISS[45]) it is most appropriate to derive trends for the part of the atmosphere nearest the surface, i.e., the lower troposphere. Doing this, through December 2019:
Comparison of data with climate models
For some time the only available satellite record was the UAH version, which (with early versions of the processing algorithm) showed a global cooling trend for its first decade. Since then, a longer record and a number of corrections to the processing have revised this picture, with both UAH and RSS measurements showing a warming trend.
A detailed analysis produced in 2005 by dozens of scientists as part of the US Climate Change Science Program (CCSP) identified and corrected errors in a variety of temperature observations, including the satellite data. Their report stated:
- "Previously reported discrepancies between the amount of warming near the surface and higher in the atmosphere have been used to challenge the reliability of climate models and the reality of human induced global warming. Specifically, surface data showed substantial global-average warming, while early versions of satellite and radiosonde data showed little or no warming above the surface. This significant discrepancy no longer exists because errors in the satellite and radiosonde data have been identified and corrected. New data sets have also been developed that do not show such discrepancies."[48]
The 2007 IPCC Fourth Assessment Report[48] states:
- "New analyses of balloon-borne and satellite measurements of lower- and mid-tropospheric temperature show warming rates that are similar to those of the surface temperature record and are consistent within their respective uncertainties, largely reconciling a discrepancy noted in the TAR."
Tropical Troposphere
Climate models predict that as the surface warms, so should the global troposphere. Globally, the troposphere (at the TLT altitude at which the MSU sounder measure) is predicted to warm about 1.2 times more than the surface; in the tropics, the troposphere should warm about 1.5 times more than the surface. However, in the 2005 CCSP report it was noted that the use of fingerprinting techniques on data yielded that "Volcanic and human-caused fingerprints were not consistently identifiable in observed patterns of lapse rate change." (Where "lapse rate" refers to the change in temperature iwith altitude). In particular, a possible inconsistency was noted in the tropics, the area in which tropospheric amplification should be most clearly seen. They stated:
- "In the tropics, the agreement between models and observations depends on the time scale considered. For month-to-month and year-to-year variations, models and observations both show amplification (i.e., the month-to-month and year-to-year variations are larger aloft than at the surface). This is a consequence of relatively simple physics, the effects of the release of latent heat as air rises and condenses in clouds. The magnitude of this amplification is very similar in models and observations. On decadal and longer time scales, however, while almost all model simulations show greater warming aloft (reflecting the same physical processes that operate on the monthly and annual time scales), most observations show greater warming at the surface.
- "These results could arise either because “real world” amplification effects on short and long time scales are controlled by different physical mechanisms, and models fail to capture such behavior; or because non-climatic influences remaining in some or all of the observed tropospheric data sets lead to biased long-term trends; or a combination of these factors. The new evidence in this Report favors the second explanation."
The most recent climate model simulations give a range of results for changes in global average temperature. Some models show more warming in the troposphere than at the surface, while a slightly smaller number of simulations show the opposite behavior. There is no fundamental inconsistency among these model results and observations at the global scale,[48] with the trends now being similar.
Globally, most climate models used by the IPCC in preparation of their third assessment in 2007 show a slightly greater warming at the TLT level than at the surface (0.03 °C/decade difference) for 1979–1999[48][49][50] while the GISS trend is +0.161 °C/decade for 1979 to 2012,[45] the lower troposphere trends calculated from satellite data by UAH and RSS are +0.130 °C/decade[22] and +0.206 °C/decade.[18]
The lower troposphere trend derived from UAH satellites (+0.128 °C/decade) is currently lower than both the GISS and Hadley Centre surface station network trends (+0.161 and +0.160 °C/decade respectively), while the RSS trend (+0.158 °C/decade) is similar. However, if the expected trend in the lower troposphere is indeed higher than the surface, then given the surface data, the troposphere trend would be around 0.194 °C/decade, making the UAH and RSS trends 66% and 81% of the expected value respectively.
Reconciliation with climate models
While the satellite data now show global warming, there is still some difference between what climate models predict and what the satellite data show for warming of the lower troposphere, with the climate models predicting slightly more warming than what the satellites measure.[51]
Both the UAH dataset and the RSS dataset have shown an overall warming trend since 1998, although the UAH retrieval shows slightly less warming than the RSS. In June 2017, RSS released v4 which significantly increased the trend seen in their data, increasing the difference between RSS and UAH trends.[52]
Atmospheric measurements taken by a different satellite measurement technique, the Atmospheric Infrared Sounder on the Aqua satellite, show close agreement with surface data.[53]
References
- "Atmospheric Soundings". Issues in the Integration of Research and Operational Satellite Systems for Climate Research: Part I. Science and Design. Washington, D.C.: National Academy Press. 2000. pp. 17–24. doi:10.17226/9963. ISBN 978-0-309-51527-6.
- Uddstrom, Michael J. (1988). "Retrieval of Atmospheric Profiles from Satellite Radiance Data by Typical Shape Function Maximum a Posteriori Simultaneous Retrieval Estimators". Journal of Applied Meteorology. 27 (5): 515–549. Bibcode:1988JApMe..27..515U. doi:10.1175/1520-0450(1988)027<0515:ROAPFS>2.0.CO;2.
- Mears, C. A. and Wentz, F. J. Upper Air Temperature, Remote Sensing Systems. Retrieved 3 Feb. 2020
- Dudhia, A. (2015). "Temperature Soundings," Encyclopedia of Atmospheric Sciences (Second Edition). Retrieved 12 January 2019.
- Christy, John R.; Spencer, Roy W.; Lobl, Elena S. (1998). "Analysis of the Merging Procedure for the MSU Daily Temperature Time Series". Journal of Climate. 11 (8): 2016–2041. Bibcode:1998JCli...11.2016.. doi:10.1175/1520-0442(1998)011<2016:AOTMPF>2.0.CO;2.
- Fu, Qiang; Johanson, Celeste M. (2005). "Satellite-derived vertical dependence of tropical tropospheric temperature trends". Geophysical Research Letters. 32 (10): L10703. Bibcode:2005GeoRL..3210703F. CiteSeerX 10.1.1.211.3632. doi:10.1029/2004GL022266. S2CID 8721786.
- The Satellite Temperature Records: Parts 1 and 2 May 1996
- Christy, John R. (2006). "Temperature Trends in the Lower Atmosphere" (PDF). CCSP sap 1.1. US Climate Change Science Program. Archived from the original (PDF) on December 24, 2010. Retrieved January 15, 2011.
- Mears, Carl A.; Wentz, Frank J. (2009). "Construction of the Remote Sensing Systems V3.2 Atmospheric Temperature Records from the MSU and AMSU Microwave Sounders". Journal of Atmospheric and Oceanic Technology. 26 (6): 1040–56. Bibcode:2009JAtOT..26.1040M. doi:10.1175/2008JTECHA1176.1.
- Spencer, Roy. "A TOVS Pathfinder Path C Product Daily 2.5 Degree Gridpoint Layer Temperatures and Oceanic Rainfall for 1979–93". Retrieved 30 April 2014.
- American Vacuum Society, Atmospheric Pressure at Different Altitudes. Retrieved 11 Jan. 2020.
- Fu, Qiang; Johanson, Celeste M. (2004). "Stratospheric Influences on MSU-Derived Tropospheric Temperature Trends: A Direct Error Analysis". Journal of Climate. 17 (24): 4636–40. Bibcode:2004JCli...17.4636F. doi:10.1175/JCLI-3267.1.
- Remote Sensing Systems Archived 2012-11-23 at the Wayback Machine
- Mears, Carl A.; Wentz, Frank J. (2005). "The Effect of Diurnal Correction on Satellite-Derived Lower Tropospheric Temperature". Science. 309 (5740): 1548–1551. Bibcode:2005Sci...309.1548M. doi:10.1126/science.1114772. PMID 16141071. S2CID 17118845.
- Remote Sensing Systems Archived 23 November 2012 at the Wayback Machine
- "RSS / MSU and AMSU Data / Description". Remote Sensing Systems. Retrieved 6 February 2017.
- "MONTHLY MEANS OF MID-TROPOSPHERE MT5.4". UAH. Archived from the original on 17 July 2012. Retrieved 13 February 2012.
- "Upper Air Temperature: Decadal Trends". remss.com. Remote Sensing Systems. Retrieved 3 February 2017.
- "RSS / MSU and AMSU Data / Time Series Trend Browser". remss.com. Retrieved 9 April 2018.
- National Environmental Satellite, Data, and Information Service (December 2010). "Microwave Sounding Calibration and Trend". National Oceanic and Atmospheric Administration. Retrieved 2012-02-13.
{{cite web}}: CS1 maint: multiple names: authors list (link) - "UW satellite trends". NOAA. Retrieved 6 February 2017.
- "UAH v6.0 TLT" (trend data at bottom of file). nsstc.uah.edu. The National Space Science & Technology Center. Retrieved 3 February 2017.
- "UAH 6.0 TMT data" (trend data at bottom of file). nsstc.uah.edu. The National Space Science and Technology Center. January 2017. Retrieved 3 February 2017.
- "MONTHLY MEANS OF LOWER STRATOSPHERE LS5.6". UAH. Retrieved 27 July 2016.
- Zou, C.; M. Goldberg; Z. Cheng; N. Grody; J. Sullivan; C. Cao; D. Tarpley (2006). "Recalibration of Microwave Sounding Unit for climate studies using simultaneous nadir overpasses". Journal of Geophysical Research. 111 (D19): D19114. Bibcode:2006JGRD..11119114Z. doi:10.1029/2005JD006798.
- Fu, Qiang; et al. (2004). "Contribution of stratospheric cooling to satellite-inferred tropospheric temperature trends" (PDF). Nature. 429 (6987): 55–58. Bibcode:2004Natur.429...55F. doi:10.1038/nature02524. PMID 15129277. S2CID 4327487.
- "State of the Climate Upper Air Annual 2011". National Oceanic and Atmospheric Administration. Retrieved 2012-02-21.
- "Climate of 2012 Annual Review". National Oceanic and Atmospheric Administration. Retrieved 30 August 2013.
- Cowtan, Kevin; Way, Robert G. (July 2014). "Coverage bias in the HadCRUT4 temperature series and its impact on recent temperature trends" (PDF). Quarterly Journal of the Royal Meteorological Society. 140 (683): 1935–1944. Bibcode:2014QJRMS.140.1935C. doi:10.1002/qj.2297. S2CID 55667548.
- Cowtan, Kevin C. and Way, Robert G. (January 6th, 2014). "Coverage bias in the HadCRUT4 temperature series and its impact on recent temperature trends. UPDATE Temperature reconstruction by domain: version 2.0 temperature series". Retrieved 15 Jan 2020.
- Cowtan, Kevin C. and Way, Robert G. Coverage bias in the HadCRUT4 temperature record, University of York, Department of Chemistry. Retrieved 15 Jan 2020.
- "Christy and Spencer Respond to Critics; Water Vapor Still Not Resolved". Cooler Heads Coalition. October 1998. Archived from the original on 2007-09-11.
- Lindzen, Richard S. (2002). "Reconciling observations of global temperature change". Geophysical Research Letters. 29 (12): 1583. Bibcode:2002GeoRL..29.1583L. doi:10.1029/2001GL014074. S2CID 2164754.
- Llanos, Miguel (2000-01-13). "Panel weighs in on global warming: Earth's surface is warmer, they say, even if upper air isn't". MSNBC. Archived from the original on 2006-04-27.
- Intergovernmental Panel on Climate Change (2001).Third Assessment Report Archived 2011-01-12 at the Wayback Machine Section 2.2.4.
- Christy, John R.; Norris, William B.; Spencer, Roy W.; Hnilo, Justin J. (2007). "Tropospheric temperature change since 1979 from tropical radiosonde and satellite measurements". Journal of Geophysical Research. 112 (D6): D06102. Bibcode:2007JGRD..112.6102C. doi:10.1029/2005JD006881.
- Climate Science: Roger Pielke Sr. Research Group Weblog Archived 2008-05-12 at the Wayback Machine
- "Archived copy" (PDF). Archived from the original (PDF) on 2010-01-15. Retrieved 2014-01-07.
{{cite web}}: CS1 maint: archived copy as title (link) - Johanson, Celeste M.; Fu, Qiang (2006). "Robustness of Tropospheric Temperature Trends from MSU Channels 2 and 4". Journal of Climate. 19 (17): 4234–42. Bibcode:2006JCli...19.4234J. CiteSeerX 10.1.1.470.3010. doi:10.1175/JCLI3866.1.
- Vinnikov, Konstantin Y.; Grody, Norman C.; Robock, Alan; Stouffer, Ronald J.; Jones, Philip D.; Goldberg, Mitchell D. (2006). "Temperature trends at the surface and in the troposphere" (PDF). Journal of Geophysical Research. 111 (D3): D03106. Bibcode:2006JGRD..111.3106V. CiteSeerX 10.1.1.143.4699. doi:10.1029/2005JD006392.
- IPCC AR5 WG1 Chapter 2, page 196.
- IPCC AR5 WG1 Chapter 9, page 772.
- "AGU – American Geophysical Union".
- "UAH adjustment". Retrieved January 15, 2011.
- "IPCC AR5 WG1 Chapter 2: Observations Atmosphere and Surface" (PDF). ipcc.ch. Intergovernmental Panel on Climate Change. 2013. p. 193. Retrieved 3 February 2017.
- Remote Sensing Services, Earth Microwave Data Center, MSU & AMSU Time Series Trend Browse Tool. Retrieved 15 Jan. 2020.
- Spencer, Roy W. (January 3, 2020). "UAH Global Temperature Update for December 2019: +0.56 deg. C". www.drroyspencer.com. Retrieved January 11, 2017.
- Tom M. L. Wigley; V. Ramaswamy; J. R. Christy; J. R. Lanzante; C. A. Mears; B. D. Santer; C. K. Folland (2 May 2006). "Executive Summary: Temperature Trends in the Lower Atmosphere – Understanding and Reconciling Differences" (PDF). United States Global Climate Change Research Program. Retrieved 26 April 2015.
- Intergovernmental Panel on Climate Change Working Group 1 (2007). "IPCC Fourth Assessment Report Summary for Policymakers" (PDF). Cambridge University Press. Retrieved 14 January 2011.
- Santer, Benjamin D.; Penner, J.E.; Thorne, P.W.; Collins, W.; Dixon, K.; Delworth, T.L.; Doutriaux, C.; Folland, C.K.; Forest, C.E.; Hansen, J.E.; Lanzante, J.R.; Meehl, G.A.; Ramaswamy, V.; Seidel, D.J.; Wehner, M.F.; Wigley, T.M.L. (April 2006). "How well can the observed vertical temperature changes be reconciled with our understanding of the causes of these changes?". In Karl, Thomas R.; Hassol, Susan J.; Miller, Christopher D.; et al. (eds.). Temperature Trends in the Lower Atmosphere: Steps for Understanding and Reconciling Differences. pp. 89–118.
- "Climate Analysis: Tropospheric Temperature". remss.com. Remote Sensing Systems. 2017. Retrieved 3 February 2017.
- Major correction to satellite data shows 140% faster warming since 1998 Carbon Brief 30 June 2017
- Harvey, Chelsea (April 18, 2019). "It's A Match: Satellite and Ground Measurements Agree on Warming", Scientific American. Retrieved 8 Jan 2019.