Mathematics education in the United States
Mathematics education in the United States varies considerably from one state to the next, and even within a single state. However, with the adoption of the Common Core Standards in most states and the District of Columbia beginning in 2010, mathematics content across the country has moved into closer agreement for each grade level. The SAT, a standardized university entrance exam, has been reformed to better reflect the contents of the Common Core.[1] However, many students take alternatives to the traditional pathways, including accelerated tracks. As of 2023, twenty-seven states require students to pass three math courses before graduation from high school, and seventeen states and the District of Columbia require four.[2]
.jpg.webp)
| This article is part of a series on |
| Education in the United States |
|---|
| Summary |
|
| Issues |
| Levels of education |
|
|
|
Compared to other developed countries in the Organisation for Economic Co-operation and Development (OECD), the average level of mathematical literacy of American students is mediocre.[3][4][5][6][7] As in many other countries, math scores dropped even further during the COVID-19 pandemic.[8] Secondary-school algebra proves to be the turning point of difficulty many students struggle to surmount,[3][9][10][11] and as such, many students are ill-prepared for collegiate STEM programs,[10][11][12] or future high-skilled careers.[13][14] Meanwhile, the number of eighth-graders enrolled in Algebra I has fallen between the early 2010s and early 2020s.[15] Across the United States, there is a shortage of qualified mathematics instructors.[16][17] Despite their best intentions, parents may transmit their mathematical anxiety to their children, who may also have school teachers who fear mathematics.[18][19] About one in five American adults are functionally innumerate.[16] While an overwhelming majority agree that mathematics is important, many, especially the young, are not confident of their own mathematical ability.[16][20]
Curricular content and standards

Each U.S. state sets its own curricular standards, and details are usually set by each local school district. Although there are no federal standards, since 2015 most states have based their curricula on the Common Core State Standards in mathematics. The stated goal of the Common Core mathematics standards is to achieve greater focus and coherence in the curriculum.[21] This is largely in response to the criticism that American mathematics curricula are "a mile wide and an inch deep."[22] The National Council of Teachers of Mathematics published educational recommendations in mathematics education in 1989 and 2000 which have been highly influential, describing mathematical knowledge, skills and pedagogical emphases from kindergarten through high school. The 2006 NCTM Curriculum Focal Points have also been influential for its recommendations of the most important mathematical topics for each grade level through grade 8. Many states either did not accept, or never adopted, the Common Core standards, but instead brought their own state standards into closer alignment with the Common Core. There has been considerable disagreement on the style and content of mathematics teaching, including the question of whether or not there should be any national standards at all.[23][24][25]
In the United States, mathematics curriculum in elementary and middle school is integrated, while in high school it traditionally has been separated by topic, with each topic usually lasting for the whole school year. However, some districts have integrated curricula, or decided to try integrated curricula after Common Core was adopted.[26][27] However, most districts follow a sequence of mathematics courses in secondary school typically called Pre-algebra, Algebra 1, Geometry, Algebra 2, Pre-calculus, and Calculus. Some schools teach Algebra 2 before Geometry. Trigonometry is usually integrated into one or several of these courses.[28] Often a course in Statistics is also offered. Calculus is only taken by a select few.[16] This traditional sequence assumes that students will pursue STEM programs in college, though, in practice, only a minority are willing and able to take this option.[16]
While a majority of schoolteachers base their lessons on a core curriculum, they do not necessarily follow them to the letter. Many also take advantage of additional resources not provided to them by their school districts.[29]
Primary school

Primary schoolchildren learn counting, arithmetic and properties of operations, geometry, measurement, statistics and probability. They typically begin studying fractions in third grade.
Secondary school
Pre-algebra can be taken in middle school. Students typically begin by learning about real numbers and basic number theory (prime numbers, prime factorization, fundamental theorem of arithmetic, ratios, and percentages), topics needed for algebra (powers, roots, graphing, order of operations, variables, expressions, and scientific notation) and geometry (quadrilaterals, polygons, areas of plane figures, the Pythagorean theorem, distance formula, equations of a line, simple solids, their surface areas, and volumes), and sometimes introductory trigonometry (definitions of the trigonometric functions). Such courses usually then go into simple algebra with solutions of simple linear equations and inequalities.
Algebra I is the first course students take in algebra. Although some students take it as eighth graders, this class is most commonly taken in ninth or tenth grade,[30] after the students have taken Pre-algebra. Students learn about real numbers and the order of operations (PEMDAS), functions, linear equations, graphs, polynomials, the factor theorem, radicals, and quadratic equations (factoring, completing the square, and the quadratic formula), and power functions.
This course is considered a gatekeeper for those who want to pursue STEM[11] because taking Algebra I in eighth grade allows students to eventually take Calculus before graduating from high school.[31] As such, tracking students by their aptitude and deciding when they should take Algebra I has become topic of controversy in California[32] and Massachusetts.[33] Parents of high-performing students are among the most vocal critics of policies discouraging the taking of Algebra I in middle school.[32][33]
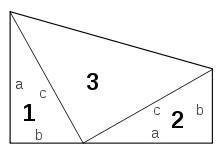
Geometry, usually taken in ninth or tenth grade, introduces students to the notion of rigor in mathematics by way of some basic concepts in mainly Euclidean geometry. Students learn the rudiments of propositional logic, methods of proof (direct and by contradiction), parallel lines, triangles (congruence and similarity), circles (secants, chords, central angles, and inscribed angles), the Pythagorean theorem, elementary trigonometry (angles of elevation and depression, the law of sines), basic analytic geometry (equations of lines, point-slope and slope-intercept forms, perpendicular lines, and vectors), and geometric probability. Students are traditionally taught to prove simple geometric theorems using two-column proofs, a method developed in the early 20th century in the U.S. specifically for this course, though other methods may also be used in some courses.[34] Depending on the curriculum and instructor, students may receive orientation towards calculus, for instance with the introduction of the method of exhaustion and Cavalieri's principle.

Algebra II has Algebra I as a prerequisite and is traditionally a high-school-level course. Course contents include inequalities, quadratic equations, power functions, exponential functions, logarithms, systems of linear equations, matrices (including matrix multiplication, matrix determinants, Cramer's rule, and the inverse of a matrix), the radian measure, graphs of trigonometric functions, trigonometric identities (Pythagorean identities, the sum-and-difference, double-angle, and half-angle formulas, the laws of sines and cosines), conic sections, among other topics.
Requiring Algebra II for high school graduation gained traction across the United States in the early 2010s.[35] The Common Core mathematical standards recognize both the sequential as well as the integrated approach to teaching high-school mathematics, which resulted in increased adoption of integrated math programs for high school. Accordingly, the organizations providing post-secondary education updated their enrollment requirements. For example, the University of California (UC) system requires three years of "college-preparatory mathematics that include the topics covered in elementary and advanced algebra and two- and three-dimensional geometry"[36] to be admitted. After the California Department of Education adopted the Common Core, the UC system clarified that "approved integrated math courses may be used to fulfill part or all"[36] of this admission requirement. On the other hand, in a controversial decision, the Texas Board of Education voted to remove Algebra II as a required course for high school graduation.[37]
In California, suggestions that Algebra II should be de-emphasized in favor of Data Science (a combination of algebra, statistics, and computer science) has faced severe criticism out of concerns that such a pathway would leave students ill-prepared for collegiate education. In 2023, the faculty of the University of California system voted to end an admissions policy that accepts Data Science in lieu of Algebra II.[32]

Precalculus follows from the above, and is usually taken by college-bound students. Pre-calculus combines algebra, analytic geometry, trigonometry, and analytic trigonometry. Topics in algebra include the binomial theorem, complex numbers, the Fundamental Theorem of Algebra, root extraction, polynomial long division, partial fraction decomposition, and matrix operations. In the chapters on analytic geometry, students are introduced to polar coordinates and deepen their knowledge of conic sections. In the components of (analytic) trigonometry, students learn the graphs of trigonometric functions, trigonometric functions on the unit circle, the dot product, the projection of one vector onto another, and how to resolve vectors. If time and aptitude permit, students might learn Heron's formula, how to calculate the determinant of a matrix via the rule of Sarrus, and the vector cross product. Students are introduced to the use of a graphing calculator to help them visualize the plots of equations and to supplement the traditional techniques for finding the roots of a polynomial, such as the rational root theorem and the Descartes rule of signs. Precalculus ends with an introduction to limits of a function. Some instructors might give lectures on mathematical induction and combinatorics in this course.[38][39][40]
AP Precalculus has only three required chapters. polynomial and rational functions, exponential and logarithmic functions, and trigonometric functions and polar curves. Optional materials include parametric equations, implicit functions, conic sections, vectors, and matrix algebra ( matrix inversion, determinants, and linear transformations).[41]
Depending on the school district, several courses may be compacted and combined within one school year, either studied sequentially or simultaneously. For example, in California, Algebra II and Precalculus may be taken as a single compressed course.[31] Without such acceleration, it may be not possible to take more advanced classes like calculus in high school.
In Oregon, high-school juniors and seniors may choose between three separate tracks, depending on their interests. Those aiming for a career in mathematics, the physical sciences, and engineering can pursue the traditional pathway, taking Algebra II and Precalculus. Those who want to pursue a career in the life sciences, the social sciences, or business can take Statistics and Mathematical Modelling. Students bound for technical training can take Applied Mathematics and Mathematical Modelling.[42] Students may also receive lessons on mathematical logic and set theory at various grade levels in high school, and this is the case in Florida, following the new 2020 reforms.[43] The new Floridian standards also promote financial literacy and emphasize how different mathematical topics from different grade levels are connected.[44]
College algebra is offered at many community colleges as remedial courses.[45] It should not be confused with abstract algebra and linear algebra, taken by students who major in mathematics and allied fields (such as computer science) in four-year colleges and universities.
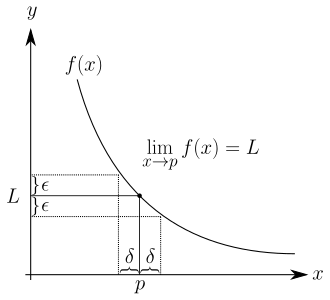
Calculus is usually taken by high-school seniors or university freshmen, but can occasionally be taken as early as tenth grade. Unlike many other countries from France to Israel to Singapore, which require high school students aiming for a career in STEM or placed in the track for advanced mathematics to study differential and integral calculus, the United States generally treats calculus as collegiate mathematics. A successfully completed college-level calculus course like one offered via Advanced Placement program (AP Calculus AB and AP Calculus BC) is a transfer-level course—that is, it can be accepted by a college as a credit towards graduation requirements. Prestigious colleges and universities are believed to require successful completion AP courses, including AP Calculus, for admissions.[46][47]
In this class, students learn about limits and continuity (the intermediate and mean value theorems), differentiation (the product, quotient, and chain rules) and its applications (implicit differentiation, logarithmic differentiation, related rates, optimization, concavity, Newton's method, L'Hôpital's rules), integration and the Fundamental Theorem of Calculus, techniques of integration (u-substitution, by parts, trigonometric and hyperbolic substitution, and by partial fractions decomposition), further applications of integration (calculating accumulated change, various problems in the sciences and engineering, separable ordinary differential equations, arc length of a curve, areas between curves, volumes and surface areas of solids of revolutions), improper integrals, numerical integration (the midpoint rule, the trapezoid rule, Simpson's rule), infinite sequences and series and their convergence (the nth-term, comparison, ratio, root, integral, p-series, and alternating series tests), Taylor's theorem (with the Lagrange remainder), Newton's generalized binomial theorem, Euler's complex identity, polar representation of complex numbers, parametric equations, and curves in polar coordinates.[48][49][50][51]
Depending on the course and instructor, special topics in introductory calculus might include the classical differential geometry of curves (arc-length parametrization, curvature, torsion, and the Frenet–Serret formulas), the epsilon-delta definition of the limit, first-order linear ordinary differential equations, Bernoulli differential equations.[48][50] Some American high schools today also offer multivariable calculus[52] (partial differentiation, the multivariable chain rule and Clairault's theorem; constrained optimization, Lagrange multipliers and the Hessian; multidimensional integration, Fubini's theorem, change of variables, and Jacobian determinants; gradients, directional derivatives, divergences, curls, the fundamental theorem of gradients, Green's theorem, Stokes' theorem, and Gauss' theorem).[48][50][51]
Other optional mathematics courses may be offered, such as statistics (including AP Statistics) or business math. Students learn to use graphical and numerical techniques to analyze distributions of data (including univariate, bivariate, and categorical data), the various methods of data collection and the sorts of conclusions one can draw therefrom, probability, and statistical inference (point estimation, confidence intervals, and significance tests).
High school students of exceptional ability may be selected to join a competition, such as the USA Mathematical Olympiad,[53][54] or the International Mathematical Olympiad.[55][56]
Tertiary school
All students in STEM, especially mathematics, physics, chemistry, computer science, and engineering must take single-variable calculus unless they have Advanced Placement credits (or equivalents, such as IB Math HL). Students majoring in mathematics, the physical sciences,[57][58] and engineering[59] then take multivariable calculus,[48][50][51] linear algebra,[60][61][62] complex variables,[63][64] ordinary differential equations,[65][66][67] and partial differential equations.[68][69][70] In addition, mathematics students study abstract algebra,[71][72] number theory,[73][74] real analysis,[75][76][77][78] advanced calculus,[79][80][81] complex analysis,[82][83][84][85] probability theory,[86] statistics,[87][88] and advanced topics, such as set theory and mathematical logic,[89][90][91][92] stochastic processes,[93] integration and measure theory,[94][95][96] Fourier analysis,[97][98] functional analysis,[99] differential geometry,[100][101][102] and topology.[103] They may further choose courses in applied mathematics, such as mathematical modelling, game theory, or mathematical optimization. The calculus of variations,[104][105][106] the history of mathematics,[107][108][109][110] and topics in theoretical or mathematical physics (such as classical mechanics,[111][105][112][113] electrodynamics,[114][115] fluid mechanics,[116][117] quantum mechanics,[118][119][120] or general relativity[121][122][123][124]) may be taken as electives. Computer science majors must take courses on discrete mathematics[125][126] (such as combinatorics and graph theory), information theory,[127] theory of computation,[128][129] and cryptography. Those who study biomedical and social sciences have to study elementary probability[130] and statistics.[131] Students in computer science and economics might have the option of taking algorithmic game theory.[132] Students in the physical sciences and engineering need to understand error analysis for their laboratory sessions and courses.[133][134] Advanced undergraduates and beginning graduate students in physics may take a course on advanced mathematical methods for physics.[135][136][137][138][139][140] Exact requirements and available courses will depend on the institution in question.
At many colleges and universities, confident students may compete in the Integration Bee.[141][142][143][144] Exceptional undergraduates may participate in the annual William Lowell Putnam Mathematical Competition.[145][146] Many successful competitors have gone on to fruitful research careers in mathematics. Although doing well on the Putnam is not a requirement for becoming a mathematician, it encourages students to develop skills and hone intuitions that could help them become successful researchers.[145][147] Besides the monetary prize, the winners are virtually guaranteed acceptance to a prestigious graduate school.[148] Such competitions are one way for mathematical talents to stand out.[149]
Attendance and completion rates
.png.webp)
For many students, passing algebra is often a Herculean challenge,[3][10][11] so much so that many students have dropped out of high school because of it.[3] The greatest obstacle for excelling in algebra is fluency with fractions, something many Americans do not have.[9] Without mastery of high-school algebra—Algebra I and II—students will not be able to pursue collegiate STEM courses.[11][10][150] From 1986 to 2012, though more students were completing Algebra II, their average performance has fallen. Indeed, students who had passed high-school courses, including those labeled "honors" courses, might still fail collegiate placement exams and had to take remedial courses.[151] As for Algebra I, the number of 13-year-olds enrolled fell from 34% in 2012 to 24% in 2023.[15]
Longitudinal analysis shows that the number of students completing high-school courses on calculus and statistics, including AP courses, have declined before 2019.[152][153] Data taken from students' transcripts () from the late 2000s to the mid-2010s reveals that majorities of students had completed Algebra I (96%), Geometry (76%), and Algebra II (62%). But not that many took Precalculus (34%), Trigonometry (16%), Calculus (19%), or Statistics (11%) and only an absolute minority took Integrated Mathematics (7%). Overall, female students were more likely to complete all mathematics courses, except Statistics and Calculus. Asian Americans were the most likely to take Precalculus (55%), Statistics (22%), and Calculus (47%) while African Americans were the least likely to complete Calculus (8%) but most likely to take Integrated Mathematics (10%) in high school.[154] Among students identified as mathematically proficient by the PSAT, Asians are much more likely than blacks to attend an honors or Advanced Placement course in mathematics.[155] Students of lower socioeconomic status were less likely to pass Precalculus, Calculus, and Statistics.[154] While boys and girls are equally likely to take AP Statistics and AP Calculus AB, boys are the majority in AP Calculus BC (59%), as well as some other highly mathematical subjects, such as AP Computer Science A (80%), AP Physics C: Mechanics (74%) and AP Physics C: Electricity and Magnetism (77%).[156] Although undergraduate men and women score the same grades in Calculus I (in college) on average, women are more likely than men to drop out because of mathematical anxiety.[157] Perceptions and stereotypes of girls being less mathematically able than boys begin as early as second grade, and they affect how girls actually perform in class or in a competition, such as the International Mathematical Olympiad.[158]
Depending on their programs, American community colleges require 60% of their students to pass at least one course in mathematics.[159] Around 80% fail to meet this requirement,[159] and 60% require remedial courses.[10] Many students at these schools drop out after failing even in remedial courses, such as (the equivalent of) Algebra II.[160]
Controversies and issues
.jpg.webp)
Mathematics education has been a topic of debate among academics, parents, as well as educators.[23][9][161][25] Majorities agree that mathematics is crucial, but there has been many divergent opinions on what kind of mathematics should be taught and whether relevance to the "real world" or rigor should be emphasized.[31][13] Another source of contention is the decentralized nature of American education, making it difficult to introduce standard curriculum implemented nationwide, despite the benefits of such a program as seen from the experience of other countries, such as Italy.[162] In the early 2020s, the decision by some educators to include the topics of race and sexuality into the mathematical curriculum has also met with stiff resistance.[163]
Progressive education
During the first half of the twentieth century, there was a movement aimed at systematically reforming American public education along more "progressive" grounds. William Heard Kilpatrick, one of the most vocal proponents of progressive education, advocated for the de-emphasis of intellectual "luxuries" such as algebra, geometry, and trigonometry, calling them "harmful rather than helpful to the kind of thinking necessary for ordinary living." He recommended that more advanced topics in mathematics should only be taught to the select few. Indeed, prior to the Second World War, it was common for educationists to argue against the teaching of academic subjects and in favor of more utilitarian concerns of "home, shop, store, citizenship, and health," presuming that a majority of high school students could not embark on a path towards higher education but were instead, destined to become unskilled laborers or their wives.[23]
By the 1940s, however, the deficiency in mathematical skills among military recruits became a public scandal. Admiral Chester Nimitz himself complained about the lack of skills that should have been taught in public schools among officers in training and volunteers. In order to address this issue, the military had to open courses to teach basic skills such as arithmetic for bookkeeping or gunnery.[23]
Indeed, many parents opposed the progressive reforms, criticizing the lack of contents. By mid-century, technological marvels, such as radar, nuclear energy, and the jet engine, made progressive education untenable.[23]
New Math

Under the 'New Math' initiative, created after the successful launch of the Soviet satellite Sputnik in 1957, conceptual abstraction rather than calculation gained a central role in mathematics education.[24] The educational status quo was severely criticized as a source of national humiliation and reforms were demanded, prompting Congress to introduce the National Defense Education Act of 1958.[23] The U.S. federal government under President Dwight D. Eisenhower realized it needed thousands of scientists and engineers to match the might of its ideological rival the Soviet Union and started pouring enormous sums of money into research and development as well as education.[164][165] Conceived in response to the lack of emphasis on content of the progressive education[23] and the technological advances of World War II,[166] New Math was part of an international movement influenced by the Nicholas Bourbaki school in France, attempting to bring the mathematics taught in schools closer to what research mathematicians actually use. Students received lessons in set theory, which is what mathematicians actually use to construct the set of real numbers, normally taught to advanced undergraduates in real analysis (see Dedekind cuts and Cauchy sequences). Arithmetic with bases other than ten was also taught (see binary arithmetic and modular arithmetic).[167] Other topics included number theory, probability theory, and analytic geometry.[166]
However, this educational initiative soon faced strong opposition, not just from teachers, who struggled to understand the new material, let alone teach it, but also from parents, who had problems helping their children with homework.[24] It was criticized by experts, too. In a 1965 essay, physicist Richard Feynman argued, "first there must be freedom of thought; second, we do not want to teach just words; and third, subjects should not be introduced without explaining the purpose or reason, or without giving any way in which the material could be really used to discover something interesting. I don't think it is worthwhile teaching such material."[168] In his 1973 book, Why Johnny Can't Add: the Failure of the New Math, mathematician and historian of mathematics Morris Kline observed that it was "practically impossible" to learn new mathematical creations without first understanding the old ones, and that "abstraction is not the first stage, but the last stage, in a mathematical development."[169] Kline criticized the authors of the 'New Math' textbooks, not for their mathematical faculty, but rather their narrow approach to mathematics, and their limited understanding of pedagogy and educational psychology.[170] Mathematician George F. Simmons wrote in the algebra section of his book Precalculus Mathematics in a Nutshell (1981) that the New Math produced students who had "heard of the commutative law, but did not know the multiplication table."[171]
By the early 1970s, this movement was defeated. Nevertheless, some of the ideas it promoted still lived on. One of the key contributions of the New Math initiative was the teaching of calculus in high school.[23]
Standards-based reforms and the NCTM
From the late twentieth century to the early twenty-first, there has been a fierce debate over how mathematics should be taught. On one hand, some campaign for a more traditional teacher-led curriculum, featuring algorithms and some memorization. On the other hand, some prefer a conceptual approach, with a focus on problem-solving and the sense of numbers.[172] However, as mathematician Hung-Hsi Wu explained, the apparent dichotomy between basic skills and understanding of mathematical concepts is a delusion.[173]
In 1989 the National Council for Teachers of Mathematics (NCTM) produced the Curriculum and Evaluation Standards for School Mathematics. Widespread adoption of the new standards notwithstanding, the pedagogical practice changed little in the United States during the 1990s.[174] In fact, mathematics education became a hotly debated subject in the 1990s and early 2000s. This debate pitted mathematicians (like UC Berkeley mathematician Hung-Hsi Wu) and parents, many of whom with substantial knowledge of mathematics (such as the Institute for Advanced Study physicist Chiara R. Nappi), who opposed the NCTM's reforms against educational professionals, who wanted to emphasized what they called "conceptual understanding." In many cases, however, educational professionals did not understand mathematics as well as their critics. This became apparent with the publication of the book Knowing and Teaching Elementary Mathematics (1999) by Liping Ma. The author gave evidence that even though most Chinese teachers had only 11 or 12 years of formal education, they understood basic mathematics better than did their U.S. counterparts, many of whom were working on their master's degrees.[23]
In 1989, the more radical NCTM reforms were eliminated. Instead, greater emphasis was put on substantive mathematics.[23] In some large school districts, this came to mean requiring some algebra of all students by ninth grade, compared to the tradition of tracking only the college-bound and the most advanced junior high school students to take algebra. A challenge with implementing the Curriculum and Evaluation Standards was that no curricular materials at the time were designed to meet the intent of the Standards. In the 1990s, the National Science Foundation funded the development of curricula such as the Core-Plus Mathematics Project. In the late 1990s and early 2000s, the so-called math wars erupted in communities that were opposed to some of the more radical changes to mathematics instruction. Some students complained that their new math courses placed them into remedial math in college.[175] However, data provided by the University of Michigan registrar at this same time indicate that in collegiate mathematics courses at the University of Michigan, graduates of Core-Plus did as well as or better than graduates of a traditional mathematics curriculum, and students taking traditional courses were also placed in remedial mathematics courses.[176] Mathematics instructor Jaime Escalante dismissed the NCTM standards as something written by a PE teacher.[23]
In 2001 and 2009, NCTM released the Principles and Standards for School Mathematics (PSSM) and the Curriculum Focal Points which expanded on the work of the previous standards documents. Particularly, the PSSM reiterated the 1989 standards, but in a more balanced way, while the Focal Points suggested three areas of emphasis for each grade level. Refuting reports and editorials[177] that it was repudiating the earlier standards, the NCTM claimed that the Focal Points were largely re-emphasizing the need for instruction that builds skills and deepens student mathematical understanding. These documents repeated the criticism that American mathematics curricula are a "mile wide and an inch deep" in comparison to the mathematics of most other nations, a finding from the Second and Third International Mathematics and Science Studies.
Integrated mathematics
Most countries teach mathematics according to what Americans call an integrated curriculum. Various aspects of calculus and prerequisites are taught throughout secondary school.[46][47] In fact, many topics in algebra and geometry that Americans typically learn in high school are taught in middle school in Europe,[162] making it possible for European countries to require and to teach calculus in high school. In France and Germany, calculus was brought into the secondary-school curriculum thanks to the advocacy of famous mathematicians, such as Henri Poincaré and Felix Klein, respectively.[46][47] However, as the Singaporean case demonstrates, early exposure to the concepts of calculus does not necessarily translates to actual understanding among high school students.[178][47] Proponents of teaching the integrated curriculum believe that students would better understand the connections between the different branches of mathematics. On the other hand, critics—including parents and teachers—prefer the traditional American approach both because of their familiarity with it and because of their concern that certain key topics might be omitted, leaving the student ill-prepared for college.[26] As mentioned above, only 7% of American high school students take Integrated mathematics.[154]
Preparation for college
Beginning in 2011, most states have adopted the Common Core Standards for mathematics, which were partially based on NCTM's previous work. Controversy still continues as critics point out that Common Core standards do not fully prepare students for college and as some parents continue to complain that they do not understand the mathematics their children are learning. Indeed, even though they may have expressed an interest in pursuing science, technology, engineering, and mathematics (STEM) in high school, many university students find themselves ill-equipped for rigorous STEM education in part because of their inadequate preparation in mathematics.[12][179] Meanwhile, Chinese, Indian, and Singaporean students are exposed to high-level mathematics and science at a young age.[12] About half of STEM students in the U.S. dropped out of their programs between 2003 and 2009.[179] On top of that, many mathematics schoolteachers were not as well-versed in their subjects as they should be, and might well be uncomfortable with mathematics themselves.[18][179][180] An emphasis on speed and rote memorization gives as many as one-third of students aged five and over mathematical anxiety.[6]
Parents and high school counselors consider it crucial that students pass Calculus if they aim to be admitted to a competitive university. Private school counselors are especially likely to make this recommendation while admissions officers are generally less inclined to consider it a requirement.[31] Moreover, there has been a movement to de-emphasize the traditional pathway with Calculus as the final mathematics class in high school in favor of Statistics and Data Science for those not planning to major in a STEM subject in college.[181] Nevertheless, Calculus remains the most recommended course for ambitious students.[181]
By the mid-2010s, only a quarter of American high school seniors are able to do grade-level math,[182] yet about half graduate from high school as A students, prompting concerns of grade inflation.[183] Strong performance in Algebra I, Geometry, and Algebra II predict good grades in university-level Calculus even better than taking Calculus in high school.[30]
Another issue with mathematics education has been integration with science education. This is difficult for public schools to do because science and math are taught independently. The value of the integration is that science can provide authentic contexts for the math concepts being taught and further, if mathematics is taught in synchrony with science, then the students benefit from this correlation.[184]
Enrichment programs and accelerated tracks

Growing numbers of parents have opted to send their children to enrichment and accelerated learning after-school or summer programs in mathematics, leading to friction with school officials who are concerned that their primary beneficiaries are affluent white and Asian families, prompting parents to pick private institutions or math circles. Some public schools serving low-income neighborhoods even denied the existence of mathematically gifted students.[179] In fact, American educators tend to focus on poorly performing students rather than those at the top, unlike their Asian counterparts.[185] Parents' proposal for an accelerated track for their children are oftentimes met with hostility by school administrators.[186] Conversely, initiatives aimed at de-emphasizing certain core subjects, such as Algebra I, triggered strong backlash from parents and university faculty members.[32][33] Students identified by the Study of Mathematically Precocious Youth as top scorers on the mathematics (and later, verbal) sections of the SAT often became highly successful in their fields.[187] By the mid-2010s, some public schools have begun offering enrichment programs to their students.[179]
Similarly, while some school districts have proposed to stop separating students by mathematical ability in order to ensure they begin high school at the same level, parents of gifted children have pushed back against this initiative, fearing that it would jeopardize their children's future college admissions prospects, especially in the STEM fields.[31][181] In San Francisco, for example, such a plan was dropped due to a combination of mixed results and public backlash.[31]
Shortage of instructors
A shortage of qualified mathematics schoolteachers has been a serious problem in the United States for many years.[16][17] In order to rectify this problem, the amount of instructional hours dedicated towards mathematical contents has been increased in undergraduate programs aimed at training elementary teachers.[188] Teachers oftentimes unknowingly transmit their own negative attitude towards mathematics to their students, damaging the quality of instruction.[180]
Standardized tests
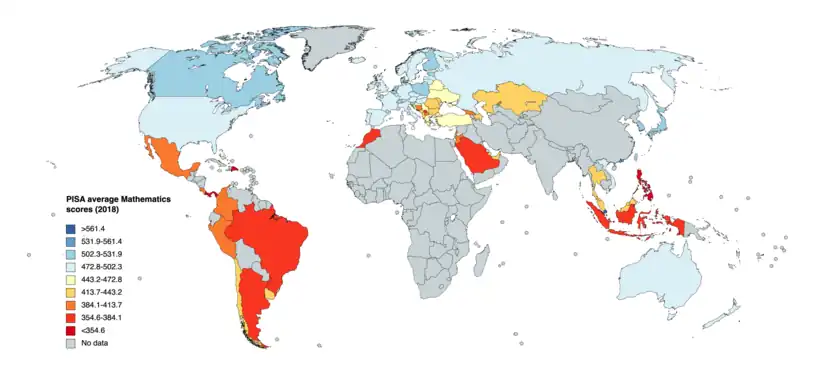
The Program for International Student Assessment (PISA) conducted the 2015 assessment test which is held every three years for 15-year-old students worldwide.[189] In 2012, the United States earned average scores in science and reading. It performed better than other progressive nations in mathematics, ranking 36 out of 65 other countries. The PISA assessment examined the students’ understanding of mathematics as well as their approach to this subject and their responses. These indicated three approaches to learning. Some of the students depended mainly on memorization. Others were more reflective on newer concepts. Another group concentrated more on principles that they have not yet studied. The U.S. had a high proportion of memorizers compared to other developed countries.[6] During the latest testing, the United States failed to make it to the top 10 in all categories including mathematics. More than 540,000 teens from 72 countries took the exam. Their average score in mathematics declined by 11 points.[5]
U.S. PISA scores broken down by race or ethnicity is shown in the table below.
| Mathematics | ||||||
|---|---|---|---|---|---|---|
| Race | 2018[190] | 2015 | 2012 | 2009 | 2006 | 2003 |
| Score | Score | Score | Score | Score | Score | |
| Asian | 539 | 498 | 549 | 524 | 494 | 506 |
| White | 503 | 499 | 506 | 515 | 502 | 512 |
| US Average | 478 | 470 | 481 | 487 | 474 | 483 |
| More than one race | 474 | 475 | 492 | 487 | 482 | 502 |
| Hispanic | 452 | 446 | 455 | 453 | 436 | 443 |
| Other | — | 423 | 436 | 460 | 446 | 446 |
| Black | 419 | 419 | 421 | 423 | 404 | 417 |
According to a 2021 report by the National Science Foundation (NSF), American students' mathematical literacy ranks 25th out of 37 nations of the Organization for Economic Cooperation and Development (OECD).[191]
During the 2000s and 2010s, as more and more college-bound students take the SAT, scores have gone down.[192][7][4] (See chart below.) This is in part because some states have required all high school students to take the SAT, regardless of whether or not they were going to college.[192]
.svg.png.webp)
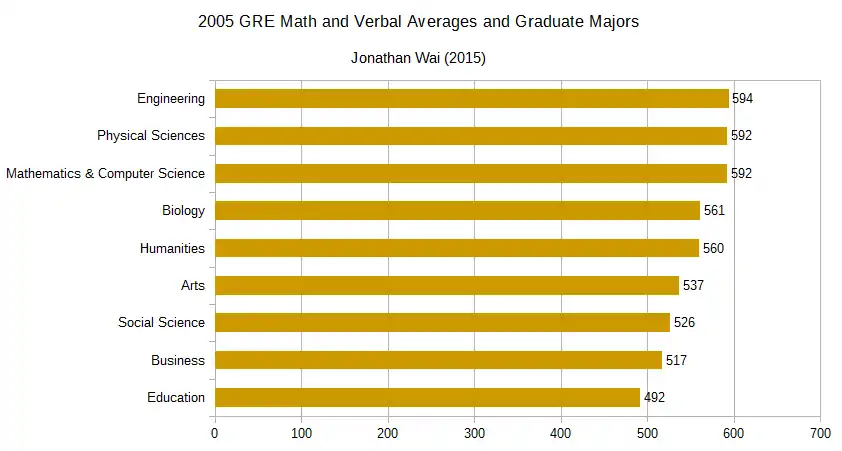
In 2015, educational psychologist Jonathan Wai of Duke University analyzed average test scores from the Army General Classification Test in 1946 (10,000 students), the Selective Service College Qualification Test in 1952 (38,420), Project Talent in the early 1970s (400,000), the Graduate Record Examination between 2002 and 2005 (over 1.2 million), and the SAT Math and Verbal in 2014 (1.6 million). Wai identified one consistent pattern: those with the highest test scores tended to pick mathematics and statistics, the natural and social sciences, and engineering as their majors while those with the lowest were more likely to choose healthcare, education, and agriculture. (See the two charts below.)[193][194]

Results from the National Assessment of Educational Progress (NAEP) test show that scores in mathematics have been leveling off in the 2010s, but with a growing gap between the top and bottom students. The COVID-19 pandemic, which forced schools to shut down and lessons to be given online, further widened the divide, as the best students lost fewer points compared to the worst and therefore could catch up more quickly.[8] While students' scores fell for all subjects, mathematics was the hardest hit, with a drop of eight points,[195] the steepest decline in 50 years.[15] Scores dropped for students of all races, sexes, socioeconomic classes, types of schools, and states with very few exceptions.[196][197] This might be because mathematics education is more dependent upon the classroom experience than reading,[197] as students who were allowed to return to in-person classes generally did better, more so in mathematics than in reading.[198] However, on the topics of statistics and probability, student performance had already declined before the pandemic.[14] As consequence, the entire cohort of college students in the 2022-23 academic year have lower average grades and mathematical standards.[199]
A 2023 comparison between parents' views and standardized test scores revealed a significant gap; most parents overestimated their children's academic aptitude. In mathematics, only 26% were proficient, even though 90% of the parents asked thought their children met grade standards.[200] Having a higher NAEP math score in eighth grade is correlated with high academic standing, higher income, lower rates of adolescent parenthood, and lower chances of criminality.[201]
Advanced Placement Mathematics
There was considerable debate about whether or not calculus should be included when the Advanced Placement (AP) Mathematics course was first proposed in the early 1950s. AP Mathematics has eventually developed into AP Calculus thanks to physicists and engineers, who convinced mathematicians of the need to expose students in these subjects to calculus early on in their collegiate programs.[52]
In the early 21st century, there has been a demand for the creation of AP Multivariable Calculus and indeed, a number of American high schools have begun to offer this class, giving colleges trouble in placing incoming students.[52]
As of 2021, AP Precalculus was under development by the College Board, though there were concerns that universities and colleges would not grant credit for such a course, given that students had previously been expected to know this material prior to matriculation.[52] AP Precalculus is scheduled to launch in Fall 2023.[202]
Conferences
Mathematics education research and practitioner conferences include: NCTM's Regional Conference and Exposition and Annual Meeting and Exposition; The Psychology of Mathematics Education's North American Chapter annual conference; and numerous smaller regional conferences.
See also
References
- Lewin, Tamar (March 5, 2014). "A New SAT Aims to Realign With Schoolwork". The New York Times. Archived from the original on May 13, 2014. Retrieved May 14, 2014.
He said he also wanted to make the test reflect more closely what students did in high school and, perhaps most important, rein in the intense coaching and tutoring on how to take the test that often gave affluent students an advantage.
- Schwartz, Sarah (January 17, 2023). "Do Students Need Four Years of High School Math?". Education Week. Archived from the original on January 26, 2023. Retrieved January 26, 2023.
- Hacker, Andrew (July 28, 2012). "Is Algebra Necessary?". The New York Times. Archived from the original on July 6, 2021. Retrieved April 24, 2023.
- Anderson, Nick (September 3, 2015). "SAT scores at lowest level in 10 years, fueling worries about high schools". The Washington Post. Retrieved September 17, 2020.
- Jackson, Abby; Kiersz, Andy (December 6, 2016). "The latest ranking of top countries in math, reading, and science is out — and the US didn't crack the top 10". Business Insider. Retrieved July 25, 2016.
- Boaler, Jo; Zoido, Pablo (2016-10-13). "Why Math Education in the U.S. Doesn't Add Up". Scientific American Mind. 27 (6): 18–19. doi:10.1038/scientificamericanmind1116-18. ISSN 1555-2284. Archived from the original on August 23, 2022.
- Hobbs, Tawnell D. (September 24, 2019). "SAT Scores Fall as More Students Take the Test". The Wall Street Journal. Archived from the original on November 28, 2020. Retrieved February 2, 2021.
- Mervosh, Sarah (September 1, 2022). "The Pandemic Erased Two Decades of Progress in Math and Reading". The New York Times. Archived from the original on September 1, 2022. Retrieved September 1, 2022.
- Lewin, Tamar (March 14, 2008). "Report Urges Changes in Teaching Math". The New York Times. Archived from the original on April 24, 2023. Retrieved April 24, 2023.
- Hanford, Emily (February 3, 2017). "Trying to Solve a Bigger Math Problem". The New York Times. Retrieved April 9, 2023.
- Schwartz, Sarah (June 22, 2021). "Algebra 1 Is a Turning Point. Here's How to Help Incoming Students". Education Week. Archived from the original on March 24, 2023. Retrieved March 24, 2023.
- Drew, Christopher (November 4, 2011). "Why Science Majors Change Their Minds (It's Just So Darn Hard)". Education Life. The New York Times. Archived from the original on 2011-11-04. Retrieved October 28, 2019.
- Cavanagh, Sean (June 7, 2007). "What Kind of Math Matters?". Education Week. Archived from the original on October 18, 2022. Retrieved April 17, 2023.
- Schwartz, Sarah (February 24, 2023). "Students' Data Literacy Is Slipping, Even as Jobs Demand the Skill". Education Week. Archived from the original on April 25, 2023. Retrieved April 25, 2023.
- Rubin, April (June 21, 2023). "Middle schoolers' reading and math scores plummet". Axios. Retrieved August 7, 2023.
- The Editorial Board (December 7, 2013). "Who Says Math Has to be Boring?". The New York Times. Archived from the original on April 30, 2023. Retrieved April 29, 2023.
- Sparks, Sarah D. (September 7, 2022). "What School Staffing Shortages Look Like Now". Education Week. Archived from the original on April 25, 2023. Retrieved April 25, 2023.
- Sparks, Sarah D. (May 16, 2011). "Researchers probe causes of math anxiety". Education Week. Archived from the original on May 3, 2023. Retrieved May 3, 2023.
- Hoffman, Jan (August 24, 2015). "Square Root of Kids' Math Anxiety: Their Parents' Help". The New York Times. Archived from the original on August 25, 2015. Retrieved April 25, 2023.
- "In a New Survey, Americans say, "We're Not Good At Math"". Change the Equation. Archived from the original on March 2, 2012. Retrieved April 29, 2023.
- "Common Core State Standards for Mathematics" (PDF). Common Core State Standards Initiative. p. 3. Retrieved February 11, 2014.
- "Mathematics". Common Core State Standards Initiative. Retrieved January 8, 2014.
- Klein, David (2003). "A Brief History of American K-12 Mathematics Education in the 20th Century". California State University, Northridge. Retrieved March 16, 2023.
- Knudson, Kevin (2015). "The Common Core is today's New Math – which is actually a good thing". The Conversation. Retrieved September 9, 2015.
- Schmidt, William H. (January 5, 2013). "The Common Core State Standards in Mathematics". Huffington Post. Retrieved March 17, 2023.
- Will, Madeline (November 10, 2014). "In Transition to Common Core, Some High Schools Turn to 'Integrated' Math". Education Week. Archived from the original on August 31, 2022. Retrieved August 31, 2022.
- Fensterwald, John. "Districts confirm they're moving ahead with Common Core". EdSource. Retrieved 18 November 2013.
- Sarikas, Christine (May 17, 2019). "The High School Math Courses You Should Take". PrepScholar. Retrieved August 18, 2023.
- Schwartz, Sarah (May 18, 2023). "What Does Math Teaching Look Like in U.S. Schools? 5 Charts Tell the Story". Education Week. Archived from the original on May 19, 2023. Retrieved May 25, 2023.
- Sparks, Sarah D. (June 28, 2021). "Doubling Down on Algebra Can Pay Off in College, But Who Your Peers Are Matters, Too". Education Week. Archived from the original on April 25, 2023. Retrieved April 25, 2023.
- Schwartz, Sarah (March 21, 2023). "San Francisco Insisted on Algebra in 9th Grade. Did It Improve Equity?". Education Week. Archived from the original on March 22, 2023. Retrieved March 23, 2023.
- Schwartz, Sarah (July 12, 2023). "California Adopts Controversial New Math Framework. Here's What's In It". Education Week. Archived from the original on July 14, 2023. Retrieved July 21, 2023.
- Huffaker, Christopher (July 14, 2023). "Cambridge schools are divided over middle school algebra". Boston Globe. Archived from the original on July 14, 2023. Retrieved July 21, 2023.
- Herbst, Patricio (2002), "Establishing a Custom of Proving in American School Geometry: Evolution of the Two-Column Proof in the Early Twentieth Century", EducationalStudiesinMathematics, 49: 283–312
- Whoriskey, Peter (April 3, 2011). "Requiring Algebra II in high school gains momentum nationwide". The Washington Post. Archived from the original on May 7, 2023. Retrieved May 6, 2023.
- "University of California admission subject requirements". Retrieved 2018-08-24.
- Loewus, Liana (January 31, 2014). "Texas Officially Drops Algebra 2 Requirement for Graduation". Education Week. Archived from the original on May 7, 2023. Retrieved May 6, 2023.
- Demana, Franklin D.; Waits, Bert K.; Foley, Gregory D.; Kennedy, Daniel (2000). Precalculus: Graphical, Numerical, Algebraic (7th ed.). Addison-Wesley. ISBN 978-0-321-35693-2.
- Simmons, George (2003). Precalculus Mathematics in a Nutshell: Geometry, Algebra, Trigonometry (Illustrated ed.). Wipf & Stock Publishers. ISBN 978-1-592-44130-3.
- Stewart, James; Redlin, Lothar; Watson, Saleem (2006). Algebra and Trigonometry (2nd ed.). Cengage Learning. ISBN 978-0-495-01357-0.
- "AP Precalculus Course Framework (Preview)" (PDF). AP Central. College Board. November 2022.
- Gewertz, Catherine (November 13, 2019). "Should High Schools Rethink How They Sequence Math Courses?". Education Week. Archived from the original on May 7, 2023. Retrieved May 6, 2023.
- "Florida B.E.S.T Standards: Mathematics" (PDF). Florida Department of Education. 2020.
- "Florida's B.E.S.T.: Here's what's next for the state's new educational standard". February 12, 2020.
- Bailey, Thomas; Dong Wook Jeong; Sung-Woo Cho (Spring 2010). "Referral, enrollment and completion in developmental education sequences in community colleges". Economics of Education Review. 29 (2): 255–270. doi:10.1016/j.econedurev.2009.09.002.
- Bressoud, David M. (2021). "The Strange Role of Calculus in the United States". ZDM – Mathematics Education. 53: 521–533.
- Bressoud, David (August 1, 2021). "Calculus Around the World". Math Values. Mathematical Association of America. Retrieved March 18, 2023.
- Thomas, George B.; Weir, Maurice D.; Hass, Joel (2010). Thomas's Calculus: Early Transcendentals (12th ed.). Addison-Wesley. ISBN 978-0-321-58876-0.
- Finney, Ross L.; Demana, Franklin D.; Waits, Bert K.; Kennedy, Daniel (2012). Calculus: Graphical, Numerical, Algebraic (4th ed.). Prentice Hall. ISBN 978-0-133-17857-9.
- Stewart, James (2012). Calculus: Early Transcendentals (7th ed.). Brooks/Cole Cengage Learning. ISBN 978-0-538-49790-9.
- Adams, Robert; Essex, Christopher (2021). Calculus: A Complete Course (10th ed.). Pearson. ISBN 978-0-135-73258-8.
- Bressoud, David (July 1, 2022). "Thoughts on Advanced Placement Precalculus". MAA Blog. Retrieved September 13, 2022.
- "United States of America Mathematical Olympiad - USAMO". The Mathematical Association of America. 2006. Archived from the original on November 6, 2006. Retrieved 2006-11-29.
- Greitzer, S. (March 1973). "The First U.S.A. Mathematical Olympiad". American Mathematical Monthly. 80 (3): 276–281. doi:10.2307/2318449. JSTOR 2318449.
- Miller, Michael E. (July 18, 2015). "Winning formula: USA tops International Math Olympiad for first time in 21 years". The Washington Post. Archived from the original on April 23, 2023. Retrieved April 27, 2023.
- Levy, Max G. (February 16, 2021). "The Coach Who Led the U.S. Math Team Back to the Top". Quanta Magazine. Retrieved April 27, 2023.
- Boas, Mary (2005). Mathematical Methods in the Physical Sciences (3rd ed.). Wiley. ISBN 978-0-471-19826-0.
- Hassani, Sadri (2008). Mathematical Methods: For Students of Physics and Related Fields (2nd ed.). Spring. ISBN 978-0-387-09503-5.
- Riley, K.F.; Hobson, Michael P.; Bence, S.J. (2006). Mathematical Methods for Physics and Engineering. Cambridge University Press. ISBN 978-0-521-67971-8.
- Strang, Gilbert (2016). Introduction to Linear Algebra (5th ed.). Wellesley-Cambridge Press. ISBN 978-0-980-23277-6.
- Axler, Sheldon (2014). Linear Algebra Done Right. Springer. ISBN 978-3-319-11079-0.
- Halmos, Paul (2017). Finite-Dimensional Vector Spaces (2nd ed.). Dover Publications. ISBN 978-0-486-81486-5.
- Spiegel, Murray R.; Lipschutz, Seymour; Schiller, John J.; Spellman, Dennis (2009). Schaum's Outline of Complex Variables (2nd ed.). McGraw-Hill Companies. ISBN 978-0-071-61569-3.
- Kwok, Yue Kuen (2010). Applied Complex Variables for Scientists and Engineers (2nd ed.). Cambridge University Press. ISBN 978-0-521-70138-9.
- Zill, Dennis G.; Wright, Warren S. (2013). Differential Equations with Boundary-Value Problems (8th ed.). Brooks/Cole Cengage Learning. ISBN 978-1-111-82706-9.
- Boyce, William E.; DiPrima, Richard C. (2012). Elementary Differential Equations and Boundary Value Problems (10th ed.). Wiley. ISBN 978-0-470-45831-0.
- Arnold, Vladimir (1978). Ordinary Differential Equations. Translated by Silverman, Richard. The MIT Press. ISBN 978-0-262-51018-9.
- Bleecker, David D.; Csordas, George (1997). Basic Partial Differential Equations. International Press of Boston. ISBN 978-1-571-46036-3.
- Asmar, Nakhlé H. (2016). Partial Differential Equations with Fourier Series and Boundary Value Problems (3rd ed.). Dover Publications. ISBN 978-0-486-80737-9.
- Strauss, Walter A. (2007). Partial Differential Equations: An Introduction. Wiley. ISBN 978-0-470-05456-7.
- Artin, Michael (2017). Algebra (2nd ed.). Pearson. ISBN 978-0-134-68960-9.
- Dummit, David S.; Foote, Richard M. (2003). Abstract Algebra (3rd ed.). Wiley. ISBN 978-0-471-43334-7.
- Scharlau, Winfried; Opolka, Hans (2010). From Fermat to Minkowski: Lectures on the Theory of Numbers and Its Historical Development. Springer-Verlag. ISBN 978-1-441-92821-4.
- Granville, Andrew (2019). Number Theory Revealed: A Masterclass. Rhode Island: American Mathematical Society. ISBN 978-1-4704-6370-0.
- Mattuck, Arthur (2013). Introduction to Analysis. CreateSpace Independent Publishing Platform. ISBN 978-1-484-81411-6.
- Bartle, Robert G.; Sherbert, Donald R. (2011). Introduction to Real Analysis (4th ed.). John Wiley & Sons, Inc. ISBN 978-0-471-43331-6.
- Abbott, Stephen (2016). Understanding Analysis (2nd ed.). Springer. ISBN 978-1-493-92711-1.
- Rudin, Walter (1976). Principles of Mathematical Analysis (3rd ed.). McGraw Hill. ISBN 978-0-070-54235-8.
- Spivak, Michael (1965). Calculus on Manifolds: A Modern Approach to Classical Theorems of Advanced Calculus. CRC Press. ISBN 978-0-367-09190-3.
- Loomis, Lynn Harold; Sternberg, Shlomo Zvi (2014). Advanced Calculus (revised ed.). World Scientific. ISBN 978-9-814-58393-0.
- Marsden, Jerrold E.; Tromba, Anthony J. (2011). Vector Calculus (6th ed.). W. H. Freeman. ISBN 978-1-429-21508-4.
- Ahlfors, Lars Valerian (1978). Complex Analysis: An Introduction to the Theory of Analytic Functions of One Complex Variable. McGraw-Hill Higher Education. ISBN 978-0-070-00657-7.
- Gamelin, Theodore W. (2001). Complex Analysis. Springer. ISBN 978-0-387-95069-3.
- Stein, Elias M.; Shakarchi, Rami (2003). Complex Analysis. Princeton University Press. ISBN 978-0-691-11385-2.
- Bak, Joseph; Newman, Donald J. (2010). Complex Analysis (3rd ed.). New York: Springer. ISBN 978-1-441-97287-3.
- Billingsley, Patrick (2012). Probability and Measure (Anniversary ed.). Wiley. ISBN 978-1-118-12237-2.
- Wackerly, Dennis D.; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7th ed.). Thomson Brooks/Cole. ISBN 978-0-495-11081-1.
- Wasserman, Larry (2003). All of Statistics: A Concise Course in Statistical Inference. Springer. ISBN 978-0-387-40272-7.
- Lipschutz, Seymour (1998). Schaum's Outline of Set Theory and Related Topics. McGraw-Hill Companies. ISBN 978-0-070-38159-9.
- Stoll, Robert Roth (1979). Set Theory and Logic. Dover Publications. ISBN 978-0-486-63829-4.
- Halmos, Paul R. (1968). Naive Set Theory. Springer. ISBN 978-0-387-90092-6.
- Rautenberg, Wolfgang (2006). A Concise Introduction to Mathematical Logic. Springer. ISBN 978-0-387-30294-2.
- Dobrow, Robert P. (2016). Introduction to Stochastic Processes with R. Wiley. ISBN 978-1-118-74065-1.
- Bartle, Robert G. (2001). A Modern Theory of Integration. American Mathematical Society. ISBN 978-0-821-80845-0.
- Stein, Elias M.; Shakarchi, Rami (2005). Real Analysis: Measure Theory, Integration, and Hilbert Spaces. Princeton University Press. ISBN 978-0-691-11386-9.
- Cohn, Donald L. (2015). Measure Theory (2nd ed.). Birkhäuser. ISBN 978-1-489-99762-3.
- Stein, Elias M.; Shakarchi, Rami (2003). Fourier Analysis: An Introduction. Princeton University Press. ISBN 978-0-691-11384-5.
- Lighthill, M.J. (1958). An Introduction to Fourier Analysis and Generalised Functions. Cambridge University Press. ISBN 978-0-521-09128-2.
- Stein, Elias M.; Shakarchi, Rami (2009). Functional Analysis: Introduction to Further Topics in Analysis. Princeton University Press. ISBN 978-0-691-11387-6.
- Sochi, Taha (2017). Introduction to Differential Geometry of Space Curves and Surfaces. CreateSpace. ISBN 978-1-546-68183-0.
- Do Carmo, Manfredo P. (2016). Differential Geometry of Curves and Surfaces. Dover Publications. ISBN 978-0-486-80699-0.
- Pressley, Andrew (2010). Elementary Differential Geometry (2nd ed.). Springer. ISBN 978-1-848-82890-2.
- Munkres, James R. (2000). Topology (2nd ed.). Pearson. ISBN 978-0-131-81629-9.
- Kot, Mark (2014). A First Course on the Calculus of Variations. American Mathematical Society. ISBN 978-1-4704-1495-5.
- Lanczos, Cornelius (1986). The Variational Principles of Mechanics (4th ed.). Dover Publications. ISBN 978-0-486-65067-8.
- Gelfand, Israel M.; Fomin, S.V. (2000). Calculus of Variations. Translated by Silverman, Richard. Dover Publications. ISBN 978-0-486-41448-5.
- Stillwell, John (2010). Mathematics and Its History (3rd ed.). Springer. ISBN 978-1-441-96052-8.
- Katz, Victor (2008). A History of Mathematics: An Introduction (3rd ed.). Addison Wesley Longman. ISBN 978-0-321-38700-4.
- Boyer, Carl B.; Merzbach, Uta C. (1991). A History of Mathematics. Wiley. ISBN 978-0-471-54397-8.
- Kline, Morris (1972). Mathematical Thought from Ancient to Modern Times. New York: Oxford University Press. ISBN 978-0-195-01496-9.
- Taylor, John R. (2005). Classical Mechanics. University Science Books. ISBN 978-1-891-38922-1.
- Goldstein, Herbert; Poole, Charles; Safko, John (2001). Classical Mechanics (3rd ed.). Pearson. ISBN 978-0-201-65702-9.
- Arnold, Vladimir (1978). Mathematical Methods of Classical Mechanics. Springer-Verlag. ISBN 978-0-387-90314-9.
- Purcell, Edward M.; Morin, David J. (2013). Electricity and Magnetism (3rd ed.). Cambridge University Press. ISBN 978-1-107-01402-2.
- Griffiths, David J. (2017). Introduction to Electrodynamics (4th ed.). Cambridge University Press. ISBN 978-1-108-42041-9.
- Batchelor, G. K. (2000). An Introduction to Fluid Dynamics. Cambridge University Press. ISBN 978-0-521-66396-0.
- Landau, Lev D.; Lifshitz, Evgeny (1987). Fluid Mechanics (2nd ed.). Butterworth-Heinemann. ISBN 978-0-750-62767-2.
- Townsend, John S. (2012). A Modern Approach to Quantum Mechanics (2nd ed.). University Science Books. ISBN 978-1-891-38978-8.
- Shankar, Ramamurti (2012). Principles of Quantum Mechanics (2nd ed.). Springer-Verlag. ISBN 978-1-475-70578-2.
- Sakurai, J. J.; Napolitano, Jim (2020). Modern Quantum Mechanics (3rd ed.). Cambridge University Press. ISBN 978-1-108-47322-4.
- Hartle, James B. (2002). Gravity: An Introduction to Einstein's General Relativity. Pearson. ISBN 978-0-805-38662-2.
- Carroll, Sean (2019). Spacetime and Geometry: An Introduction to General Relativity. Cambridge University Press. ISBN 978-1-108-48839-6.
- Misner, Charles; Thorne, Kip; Wheeler, John (2017). Gravitation. Princeton University Press. ISBN 978-0-691-17779-3.
- Wald, Robert (1984). General Relativity. The University of Chicago Press. ISBN 978-0-226-87033-5.
- Graham, Ronald L.; Knuth, Donald; Patashnik, Oren (1994). Concrete Mathematics: A Foundation for Computer Science (2nd ed.). Addison-Wesley Professional. ISBN 978-0-201-55802-9.
- Rosen, Kenneth H. (2018). Discrete Mathematics and Its Applications (8th ed.). McGraw-Hill. ISBN 978-1-259-67651-2.
- Cover, Thomas M.; Thomas, Joy A. (2006). Elements of Information Theory (2nd ed.). Wiley-Interscience. ISBN 978-0-471-24195-9.
- Sipser, Michael (1996). Introduction to the Theory of Computation (3rd ed.). Cengage Learning. ISBN 978-1-133-18779-0.
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009). Introduction to Algorithms (3rd ed.). The MIT Press. ISBN 978-0-262-03384-8.
- Gross, Benedict; Harris, Joseph; Riehl, Emily (2019). Fat Chance: Probability from 0 to 1. Cambridge University Press. ISBN 978-1-108-72818-8.
- Johnson, Robert; Kuby, Patricia (2003). Just the Essentials of Elementary Statistics (3rd ed.). Thomson Brooks/Cole. ISBN 0-534-38472-2.
- Roughgarden, Tim (2016). Twenty Lectures on Algorithmic Game Theory. Cambridge University Press. ISBN 978-1-107-17266-1.
- Taylor, John R. (1996). Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements (2nd ed.). University Science Books. ISBN 978-0-93570-275-0.
- Hughes, Ifan G.; Hase, Thomas P. A. (2013). Measurements and their Uncertainties: A Practical Guide to Modern Error Analysis. Oxford: Oxford University Press. ISBN 978-0-19-956633-4.
- Weber, Hans J.; Harris, Frank E.; Arfken, George B. (2012). Mathematical Methods for Physicists (7th ed.). Elsevier Science & Technology. ISBN 978-9-381-26955-8.
- Hassani, Sadri (2013). Mathematical Physics: A Modern Introduction to Its Foundations (2nd ed.). Springer. ISBN 978-3-319-01194-3.
- Neuenschwander, Dwight E. (2014). Tensor Calculus for Physics: A Concise Guide. Johns Hopkins University Press. ISBN 978-1-421-41565-9.
- Jeevanjee, Nadir (2015). An Introduction to Tensors and Group Theory for Physicists (2nd ed.). Boston: Birkhäuser. ISBN 978-3-319-14793-2.
- Zee, Anthony (2016). Group Theory in a Nutshell for Physicists (Illustrated ed.). Princeton University Press. ISBN 978-0-691-16269-0.
- Bender, Carl; Orszag, Steven A. (2010). Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory. Springer. ISBN 978-1-441-93187-0.
- Baker, Billy (January 20, 2012). "An integral part of MIT life". Boston Globe. Retrieved February 6, 2021.
- "Integration Bee". AMS Student Chapter, University of Connecticut. 2018. Retrieved February 6, 2021.
- "WVU Integration Bee Competition". School of Mathematical and Data Sciences, West Virginia University. 2023. Retrieved May 4, 2023.
- "Integration Bee". Berekley SPS. University of California, Berkeley. Retrieved February 6, 2021.
- Miller, Sandi (March 3, 2020). "MIT students dominate annual Putnam Mathematical Competition". MIT News. Retrieved April 27, 2023.
- Jiang, Georgia (February 27, 2023). "UMD Students Win Fourth Place in Putnam Mathematical Competition". Maryland Today. University of Maryland. Retrieved April 27, 2023.
- Shelton, Jim (March 29, 2023). "Yale team excels at Putnam student mathematics competition". Yale Daily News. Retrieved May 7, 2023.
- Nasar, Sylvia (1998). "2: Carnegie Institute of Technology". A Beautiful Mind. New York: Simon & Shuster. pp. 43–44. ISBN 0-7432-2457-4.
- Miller, Sandi (March 27, 2019). "Solving for fun (and sometimes prizes)". MIT News. Retrieved May 6, 2023.
- "A Leak in the STEM Pipeline: Taking Algebra Early". U.S. Department of Education. November 2018. Retrieved May 13, 2023.
- Robelen, Erik W. (September 4, 2013). "Algebra 2: Not the Same Credential It Used to Be?". Education Week. Archived from the original on May 7, 2023. Retrieved May 6, 2023.
- Bressoud, David (September 1, 2022). "The Decline of High School Calculus". Math Values. Mathematical Association of America. Retrieved March 18, 2023.
- "AP Exam Volume Change (2009-2019)" (PDF). AP Data Archive. College Board. 2019.
- Champion, Joe; Mesa, Vilma (2017). "Factors Affecting Calculus Completion among U.S. High School Students". In Bressoud, David (ed.). The Role of Calculus in the Transition from High School to College Mathematics (PDF). Washington, D.C.: MAA and NCTM. pp. 9–25.
- Quinton, Sophie (December 11, 2014). "The Race Gap in High School Honors Classes". The Atlantic. Archived from the original on April 2, 2021. Retrieved May 17, 2023.
- Robelen, Erik W. (February 15, 2012). "Girls Like Biology, Boys Like Physics? AP Data Hint at Preferences". Education Week. Archived from the original on April 30, 2023. Retrieved April 30, 2023.
- Loewus, Liana (August 3, 2016). "What's Keeping Women Out of Science, Math Careers? Calculus and Confidence". Education Week. Archived from the original on April 30, 2023. Retrieved April 30, 2023.
- Whitney, A.K. (April 18, 2016). "Math for Girls, Math for Boys". The Atlantic. Archived from the original on April 4, 2021. Retrieved May 2, 2023.
- Lattimore, Kayla; Depenbrock, Julie (July 19, 2017). "Say Goodbye To X+Y: Should Community Colleges Abolish Algebra?". NPR. Retrieved April 9, 2023.
- Quinton, Sophie (October 29, 2013). "Algebra Doesn't Have to Be Scary". The Atlantic. Archived from the original on July 8, 2022. Retrieved May 2, 2023.
- Stephanie Banchero (May 8, 2012). "School-standards pushback". The Wall Street Journal. Retrieved March 23, 2013.
- Nappi, Chiara (May 1990). "On Mathematics and Science Education in the US and Europe". Physics Today. 43 (5): 77. Bibcode:1990PhT....43e..77N. doi:10.1063/1.2810564.
- Blad, Evie (April 17, 2023). "Parents, Teachers Agree: Math Matters, But Schools Must Make It Relevant". Education Week. Archived from the original on April 17, 2023. Retrieved April 17, 2023.
- Garraty, John A. (1991). "Chapter XXXII Society in Flux, 1945-1980. Rethinking Public Education". The American Nation: A History of the United States. United States of America: Harper Collins. pp. 896–7. ISBN 978-0-06-042312-4.
- Farmelo, Graham (2009). "Twenty-six: 1958-1962". The Strangest Man: the Hidden Life of Paul Dirac, Mystic of the Atom. Basic Books. p. 363. ISBN 978-0-465-02210-6.
- Gandel, Stephen (May 30, 2015). "This 1958 Fortune article introduced the world to John Nash and his math". Fortune. Retrieved March 16, 2023.
- Gispert, Hélène. "L'enseignement des mathématiques au XXe siècle dans le contexte français". CultureMATH (in French). Archived from the original on July 15, 2017. Retrieved November 4, 2020.
- Feynman, Richard P. (1965). "New Textbooks for the 'New' Mathematics" (PDF). Engineering and Science. XXVIII (6): 9–15. ISSN 0013-7812.
- Kline, Morris (1973). Why Johnny Can't Add: The Failure of the New Math. New York: St. Martin's Press. pp. 17, 98. ISBN 0-394-71981-6.
- Gillman, Leonard (May 1974). "Review of Why Johnny Can't Add". American Mathematical Monthly. 81 (5): 531–2. JSTOR 2318615.
- Simmons, George F. (2003). "Algebra – Introduction". Precalculus Mathematics in a Nutshell: Geometry, Algebra, Trigonometry: Geometry, Algebra, Trigonometry. Wipf and Stock Publishers. p. 33. ISBN 9781592441303.
- "America's Maths Wars". The Economist. November 6, 2021. Archived from the original on November 4, 2021. Retrieved August 23, 2022.
- Wu, Hung-Hsi (Fall 1999). "Basic Skills Versus Conceptual Understanding: A Bogus Dichotomy in Mathematics Education" (PDF). American Educator. American Federation of Teachers.
- Hiebert, James; Stigler, James W. (September 2000). "A proposal for improving classroom teaching: Lessons from the TIMSS video study". The Elementary School Journal. 101 (1): 3–20. doi:10.1086/499656.
- Christian Science Monitor Archived 2008-05-09 at the Wayback Machine
- "Frequently Asked Questions About the Core-Plus Mathematics Project". Archived from the original on 2010-08-21. Retrieved 2009-10-26.
- Wall Street Journal, New York Times, Chicago Sun Times
- Toh, Tin Lam (2021). "School calculus curriculum and the Singapore mathematics curriculum framework". ZDM – Mathematics Education. 53: 535–547.
- Tyre, Peg (February 8, 2016). "The Math Revolution". The Atlantic. Archived from the original on June 28, 2020. Retrieved February 4, 2021.
- Sparks, Sarah D. (January 7, 2020). "The Myth Fueling Math Anxiety". Education Week. Archived from the original on August 31, 2022. Retrieved August 31, 2022.
- Schwartz, Sarah (September 7, 2022). "Why Elite College Admissions May Play an Outsized Role in K-12 Math Programs". Education Week. Archived from the original on September 10, 2022.
- Gonser, Sarah (April 12, 2018). "Students are being prepared for jobs that no longer exist. Here's how that could change". Culture Matters. NBC News. Retrieved October 25, 2019.
- Wang, Amy X. (July 19, 2017). "No wonder young Americans feel so important, when half of them finish high school as A students". Quartz. Archived from the original on June 19, 2021.
- Furner, Joseph M., and Kumar, David D. , "The Mathematics and Science Integration Argument: A Stand for Teacher Education," Eurasia Journal of Mathematics, Science & Technology Education, Vol. 3, Num. 3, August, 2007, accessed on 15 December 2013
- Clynes, Tom (September 7, 2016). "How to raise a genius: lessons from a 45-year study of super-smart children". Nature. 537 (7619): 152–155. Bibcode:2016Natur.537..152C. doi:10.1038/537152a. PMID 27604932. S2CID 4459557.
- Matthews, Jay (September 10, 2022). "Middle schools shun challenges, such as teaching your kid algebra". The Washington Post. Archived from the original on September 12, 2022. Retrieved April 29, 2023.
- Clynes, Tom (January 2017). "Nurturing Genius". Scientific American. Archived from the original on December 23, 2016.
- Will, Madaline (May 18, 2022). "Are Aspiring Elementary Teachers Learning Enough Math?". Education Week. Archived from the original on August 31, 2022. Retrieved May 10, 2023.
- "What the world can learn from the latest PISA test results". The Economist. Retrieved 2018-07-25.
- "Highlights of U.S. PISA 2018 Results Web Report" (PDF).
- Rotermund, Susan; Burke, Amy (July 8, 2021). "Elementary and Secondary STEM Education - Executive Summary". National Science Foundation. Retrieved January 27, 2023.
- Finder, Alan (August 28, 2007). "Math and Reading SAT Scores Drop". The New York Times. Archived from the original on April 24, 2023. Retrieved April 24, 2023.
- Wai, Jonathan (February 3, 2015). "Your college major is a pretty good indication of how smart you are". Quartz. Archived from the original on January 16, 2020. Retrieved January 30, 2021.
- Crew, Bec (February 16, 2015). "Your College Major Can Be a Pretty Good Indication of How Smart You Are". Humans. Science Magazine. Retrieved January 30, 2021.
- Binkey, Collin (October 24, 2022). "Test scores show how COVID set kids back across the U.S." PBS Newshour. Retrieved December 31, 2022.
- Sparks, Sarah D. (October 24, 2022). "Explaining That Steep Drop in Math Scores on NAEP: 5 Takeaways". Education Week. Archived from the original on March 20, 2023. Retrieved April 25, 2023.
- Chapman, Ben (October 24, 2022). "Math Scores Dropped in Every State During Pandemic, Report Card Shows". The Wall Street Journal. Archived from the original on October 24, 2022. Retrieved May 18, 2023.
- Lasarte, Diego (May 3, 2023). "US eighth graders' history test scores hit lowest levels on record". Quartz. Archived from the original on May 19, 2023. Retrieved May 18, 2023.
- Fawcett, Eliza (November 1, 2022). "The Pandemic Generation Goes to College. It Has Not Been Easy". The New York Times. Archived from the original on November 1, 2022. Retrieved May 25, 2023.
- Nawaz, Amna; Cuevas, Karina (April 6, 2023). "Study shows parents overestimate their student's academic progress". PBS Newshour. Retrieved April 9, 2023.
- Doty, Elena; Kane, Thomas J.; Patterson, Tyler; Staiger, Douglas O. (December 2022). "What Do Changes in State Test Scores Imply for Later Life Outcomes?". NBER Working Papers. National Bureau of Economic Research. doi:10.3386/w30701.
- Najarro, Ileana (May 19, 2022). "A New AP Precalculus Course Aims to Diversify the Math Pipeline". Education Week. Archived from the original on March 24, 2023.
Further reading
- Garelick, Barry; Wilson, JR (2022). Traditional Math: An effective strategy that teachers feel guilty using. John Catt Educational. ISBN 978-1-91526-154-0.
External links
- Math courses with “Math Is Your Future”; an article about studying math with the use of Internet technologies
- Math is amazing and we have to start treating it that way, Eugenia Cheng for the PBS Newshour.