Mean value theorem
In mathematics, the mean value theorem (or Lagrange theorem) states, roughly, that for a given planar arc between two endpoints, there is at least one point at which the tangent to the arc is parallel to the secant through its endpoints. It is one of the most important results in real analysis. This theorem is used to prove statements about a function on an interval starting from local hypotheses about derivatives at points of the interval.
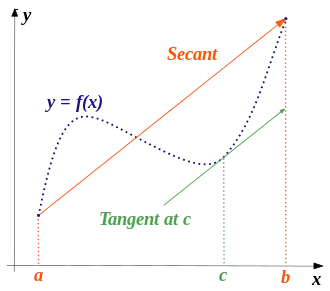
More precisely, the theorem states that if is a continuous function on the closed interval and differentiable on the open interval , then there exists a point in such that the tangent at is parallel to the secant line through the endpoints and , that is,
History
A special case of this theorem for inverse interpolation of the sine was first described by Parameshvara (1380–1460), from the Kerala School of Astronomy and Mathematics in India, in his commentaries on Govindasvāmi and Bhāskara II.[1] A restricted form of the theorem was proved by Michel Rolle in 1691; the result was what is now known as Rolle's theorem, and was proved only for polynomials, without the techniques of calculus. The mean value theorem in its modern form was stated and proved by Augustin Louis Cauchy in 1823.[2] Many variations of this theorem have been proved since then.[3][4]
Formal statement
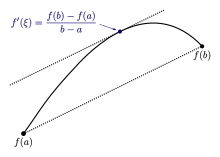

Let be a continuous function on the closed interval , and differentiable on the open interval , where . Then there exists some in such that
The mean value theorem is a generalization of Rolle's theorem, which assumes , so that the right-hand side above is zero.
The mean value theorem is still valid in a slightly more general setting. One only needs to assume that is continuous on , and that for every in the limit
exists as a finite number or equals or . If finite, that limit equals . An example where this version of the theorem applies is given by the real-valued cube root function mapping , whose derivative tends to infinity at the origin.
The theorem, as stated, is false if a differentiable function is complex-valued instead of real-valued. For example, define for all real . Then
while for any real .
These formal statements are also known as Lagrange's Mean Value Theorem.[5]
Proof
The expression gives the slope of the line joining the points and , which is a chord of the graph of , while gives the slope of the tangent to the curve at the point . Thus the mean value theorem says that given any chord of a smooth curve, we can find a point on the curve lying between the end-points of the chord such that the tangent of the curve at that point is parallel to the chord. The following proof illustrates this idea.
Define , where is a constant. Since is continuous on and differentiable on , the same is true for . We now want to choose so that satisfies the conditions of Rolle's theorem. Namely
By Rolle's theorem, since is differentiable and , there is some in for which , and it follows from the equality that,
Implications
Theorem 1: Assume that f is a continuous, real-valued function, defined on an arbitrary interval I of the real line. If the derivative of f at every interior point of the interval I exists and is zero, then f is constant in the interior.
Proof: Assume the derivative of f at every interior point of the interval I exists and is zero. Let (a, b) be an arbitrary open interval in I. By the mean value theorem,[6] there exists a point c in (a, b) such that
This implies that f(a) = f(b). Thus, f is constant on the interior of I and thus is constant on I by continuity. (See below for a multivariable version of this result.)
Remarks:
- Only continuity of f, not differentiability, is needed at the endpoints of the interval I. No hypothesis of continuity needs to be stated if I is an open interval, since the existence of a derivative at a point implies the continuity at this point. (See the section continuity and differentiability of the article derivative.)
- The differentiability of f can be relaxed to one-sided differentiability, a proof given in the article on semi-differentiability.
Theorem 2: If f' (x) = g' (x) for all x in an interval (a, b) of the domain of these functions, then f - g is constant, i.e. f = g + c where c is a constant on (a, b).
Proof: Let F = f − g, then F' = f' − g' = 0 on the interval (a, b), so the above theorem 1 tells that F = f − g is a constant c or f = g + c.
Theorem 3: If F is an antiderivative of f on an interval I, then the most general antiderivative of f on I is F(x) + c where c is a constant.
Proof: It directly follows from the theorem 2 above.
Cauchy's mean value theorem
Cauchy's mean value theorem, also known as the extended mean value theorem,[7] is a generalization of the mean value theorem. It states: if the functions and are both continuous on the closed interval and differentiable on the open interval , then there exists some , such that[5]
Of course, if and , this is equivalent to:
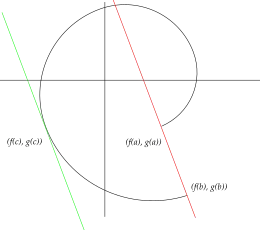
Geometrically, this means that there is some tangent to the graph of the curve[8]
which is parallel to the line defined by the points and . However, Cauchy's theorem does not claim the existence of such a tangent in all cases where and are distinct points, since it might be satisfied only for some value with , in other words a value for which the mentioned curve is stationary; in such points no tangent to the curve is likely to be defined at all. An example of this situation is the curve given by
which on the interval goes from the point to , yet never has a horizontal tangent; however it has a stationary point (in fact a cusp) at .
Cauchy's mean value theorem can be used to prove L'Hôpital's rule. The mean value theorem is the special case of Cauchy's mean value theorem when .
Proof of Cauchy's mean value theorem
The proof of Cauchy's mean value theorem is based on the same idea as the proof of the mean value theorem.
-
Suppose . Define , where is fixed in such a way that , namely
Since and are continuous on and differentiable on , the same is true for . All in all, satisfies the conditions of Rolle's theorem: consequently, there is some in for which . Now using the definition of we have:
Therefore:
which implies the result.[5]
- If , then, applying Rolle's theorem to , it follows that there exists in for which . Using this choice of , Cauchy's mean value theorem (trivially) holds.
Generalization for determinants
Assume that and are differentiable functions on that are continuous on . Define
There exists such that .
Notice that
and if we place , we get Cauchy's mean value theorem. If we place and we get Lagrange's mean value theorem.
The proof of the generalization is quite simple: each of and are determinants with two identical rows, hence . The Rolle's theorem implies that there exists such that .
Mean value theorem in several variables
The mean value theorem generalizes to real functions of multiple variables. The trick is to use parametrization to create a real function of one variable, and then apply the one-variable theorem.
Let be an open subset of , and let be a differentiable function. Fix points such that the line segment between lies in , and define . Since is a differentiable function in one variable, the mean value theorem gives:
for some between 0 and 1. But since and , computing explicitly we have:
where denotes a gradient and a dot product. This is an exact analog of the theorem in one variable (in the case this is the theorem in one variable). By the Cauchy–Schwarz inequality, the equation gives the estimate:
In particular, when the partial derivatives of are bounded, is Lipschitz continuous (and therefore uniformly continuous).
As an application of the above, we prove that is constant if the open subset is connected and every partial derivative of is 0. Pick some point , and let . We want to show for every . For that, let . Then E is closed and nonempty. It is open too: for every ,
for every in some neighborhood of . (Here, it is crucial that and are sufficiently close to each other.) Since is connected, we conclude .
The above arguments are made in a coordinate-free manner; hence, they generalize to the case when is a subset of a Banach space.
Mean value theorem for vector-valued functions
There is no exact analog of the mean value theorem for vector-valued functions (see below). However, there is an inequality which can be applied to many of the same situations to which the mean value theorem is applicable in the one dimensional case:[9]
Theorem — For a continuous vector-valued function differentiable on , there exists a number such that
- .
The theorem follows from the mean value theorem. Indeed, take . Then is real-valued and thus, by the mean value theorem,
for some . Now, and Hence, using the Cauchy–Schwarz inequality, from the above equation, we get:
If , the theorem is trivial (any c works). Otherwise, dividing both sides by yields the theorem.
Jean Dieudonné in his classic treatise Foundations of Modern Analysis discards the mean value theorem and replaces it by mean inequality (which is given below) as the proof is not constructive and one cannot find the mean value and in applications one only needs mean inequality. Serge Lang in Analysis I uses the mean value theorem, in integral form, as an instant reflex but this use requires the continuity of the derivative. If one uses the Henstock–Kurzweil integral one can have the mean value theorem in integral form without the additional assumption that derivative should be continuous as every derivative is Henstock–Kurzweil integrable.
The reason why there is no analog of mean value equality is the following: If f : U → Rm is a differentiable function (where U ⊂ Rn is open) and if x + th, x, h ∈ Rn, t ∈ [0, 1] is the line segment in question (lying inside U), then one can apply the above parametrization procedure to each of the component functions fi (i = 1, …, m) of f (in the above notation set y = x + h). In doing so one finds points x + tih on the line segment satisfying
But generally there will not be a single point x + t*h on the line segment satisfying
for all i simultaneously. For example, define:
Then , but and are never simultaneously zero as ranges over .
The above theorem implies the following:
Mean value inequality — [10] For a continuous function , if is differentiable on , then
- .
In fact, the above statement suffices for many applications and can be proved directly as follows. (We shall write for for readability.) First assume is differentiable at too. If is unbounded on , there is nothing to prove. Thus, assume . Let be some real number. Let
We want to show . By continuity of , the set is closed. It is also nonempty as is in it. Hence, the set has the largest element . If , then and we are done. Thus suppose otherwise. For ,
Let be such that . By the differentiability of at (note may be 0), if is sufficiently close to , the first term is . The second term is . The third term is . Hence, summing the estimates up, we get: , a contradiction to the maximality of . Hence, and that means:
Since is arbitrary, this then implies the assertion. Finally, if is not differentiable at , let and apply the first case to restricted on , giving us:
since . Letting finishes the proof.
For some applications of mean value inequality to establish basic results in calculus, see also Calculus on Euclidean space#Basic notions.
A certain type of generalization of the mean value theorem to vector-valued functions is obtained as follows: Let f be a continuously differentiable real-valued function defined on an open interval I, and let x as well as x + h be points of I. The mean value theorem in one variable tells us that there exists some t* between 0 and 1 such that
On the other hand, we have, by the fundamental theorem of calculus followed by a change of variables,
Thus, the value f′(x + t*h) at the particular point t* has been replaced by the mean value
This last version can be generalized to vector valued functions:
Proposition — Let U ⊂ Rn be open, f : U → Rm continuously differentiable, and x ∈ U, h ∈ Rn vectors such that the line segment x + th, 0 ≤ t ≤ 1 remains in U. Then we have:
where Df denotes the Jacobian matrix of f and the integral of a matrix is to be understood componentwise.
Proof. Let f1, …, fm denote the components of f and define:
Then we have
The claim follows since Df is the matrix consisting of the components .
The mean value inequality can then be obtained as a corollary of the above proposition (though under the assumption the derivatives are continuous).[11]
Cases where the theorem cannot be applied
Both conditions for the mean value theorem are necessary:
- is differentiable on
- is continuous on
Where one of the above conditions is not satisfied, the mean value theorem is not valid in general, and so it cannot be applied.
Function is differentiable on open interval a,b
The necessity of the first condition can be seen by the counterexample where the function on [-1,1] is not differentiable.
Function is continuous on closed interval a,b
The necessity of the second condition can be seen by the counterexample where the function
satisfies criteria 1 since on
But not criteria 2 since and for all so no such exists

Mean value theorems for definite integrals
First mean value theorem for definite integrals

Let f : [a, b] → R be a continuous function. Then there exists c in (a, b) such that
Since the mean value of f on [a, b] is defined as
we can interpret the conclusion as f achieves its mean value at some c in (a, b).[13]
In general, if f : [a, b] → R is continuous and g is an integrable function that does not change sign on [a, b], then there exists c in (a, b) such that
Proof that there is some c in [a, b][14]
Suppose f : [a, b] → R is continuous and g is a nonnegative integrable function on [a, b]. By the extreme value theorem, there exists m and M such that for each x in [a, b], and . Since g is nonnegative,
Now let
If , we're done since
means
so for any c in (a, b),
If I ≠ 0, then
By the intermediate value theorem, f attains every value of the interval [m, M], so for some c in [a, b]
that is,
Finally, if g is negative on [a, b], then
and we still get the same result as above.
QED
Second mean value theorem for definite integrals
There are various slightly different theorems called the second mean value theorem for definite integrals. A commonly found version is as follows:
- If G : [a, b] → R is a positive monotonically decreasing function and φ : [a, b] → R is an integrable function, then there exists a number x in (a, b] such that
Here stands for , the existence of which follows from the conditions. Note that it is essential that the interval (a, b] contains b. A variant not having this requirement is:[15]
- If G : [a, b] → R is a monotonic (not necessarily decreasing and positive) function and φ : [a, b] → R is an integrable function, then there exists a number x in (a, b) such that
Mean value theorem for integration fails for vector-valued functions
If the function returns a multi-dimensional vector, then the MVT for integration is not true, even if the domain of is also multi-dimensional.
For example, consider the following 2-dimensional function defined on an -dimensional cube:
Then, by symmetry it is easy to see that the mean value of over its domain is (0,0):
However, there is no point in which , because everywhere.
A probabilistic analogue of the mean value theorem
Let X and Y be non-negative random variables such that E[X] < E[Y] < ∞ and (i.e. X is smaller than Y in the usual stochastic order). Then there exists an absolutely continuous non-negative random variable Z having probability density function
Let g be a measurable and differentiable function such that E[g(X)], E[g(Y)] < ∞, and let its derivative g′ be measurable and Riemann-integrable on the interval [x, y] for all y ≥ x ≥ 0. Then, E[g′(Z)] is finite and[16]
Mean value theorem in complex variables
As noted above, the theorem does not hold for differentiable complex-valued functions. Instead, a generalization of the theorem is stated such:[17]
Let f : Ω → C be a holomorphic function on the open convex set Ω, and let a and b be distinct points in Ω. Then there exist points u, v on the interior of the line segment from a to b such that
Where Re() is the real part and Im() is the imaginary part of a complex-valued function.
See also
Notes
- J. J. O'Connor and E. F. Robertson (2000). Paramesvara, MacTutor History of Mathematics archive.
- Ádám Besenyei. "Historical development of the mean value theorem" (PDF).
- Lozada-Cruz, German (2020-10-02). "Some variants of Cauchy's mean value theorem". International Journal of Mathematical Education in Science and Technology. 51 (7): 1155–1163. Bibcode:2020IJMES..51.1155L. doi:10.1080/0020739X.2019.1703150. ISSN 0020-739X. S2CID 213335491.
- Sahoo, Prasanna. (1998). Mean value theorems and functional equations. Riedel, T. (Thomas), 1962-. Singapore: World Scientific. ISBN 981-02-3544-5. OCLC 40951137.
- Kirshna's Real Analysis: (General). Krishna Prakashan Media.
- "Mean Value Theorem". keepnotes.com.
- W., Weisstein, Eric. "Extended Mean-Value Theorem". mathworld.wolfram.com. Retrieved 2018-10-08.
{{cite web}}: CS1 maint: multiple names: authors list (link) - "Cauchy's Mean Value Theorem". Math24. Retrieved 2018-10-08.
- Rudin, Walter (1976). Principles of Mathematical Analysis (3rd ed.). New York: McGraw-Hill. p. 113. ISBN 978-0-07-054235-8. Theorem 5.19.
- Hörmander 2015, Theorem 1.1.1. and remark following it.
- Lemma — Let v : [a, b] → Rm be a continuous function defined on the interval [a, b] ⊂ R. Then we haveProof. Let u in Rm denote the value of the integralMean Value Inequality — If the norm of Df(x + th) is bounded by some constant M for t in [0, 1], thenProof.
- "Mathwords: Mean Value Theorem for Integrals". www.mathwords.com.
- Michael Comenetz (2002). Calculus: The Elements. World Scientific. p. 159. ISBN 978-981-02-4904-5.
- Editorial note: the proof needs to be modified to show there is a c in (a, b)
- Hobson, E. W. (1909). "On the Second Mean-Value Theorem of the Integral Calculus". Proc. London Math. Soc. S2–7 (1): 14–23. Bibcode:1909PLMS...27...14H. doi:10.1112/plms/s2-7.1.14. MR 1575669.
- Di Crescenzo, A. (1999). "A Probabilistic Analogue of the Mean Value Theorem and Its Applications to Reliability Theory". J. Appl. Probab. 36 (3): 706–719. doi:10.1239/jap/1032374628. JSTOR 3215435. S2CID 250351233.
- 1 J.-Cl. Evard, F. Jafari, A Complex Rolle’s Theorem, American Mathematical Monthly, Vol. 99, Issue 9, (Nov. 1992), pp. 858-861.
References
- Hörmander, Lars (2015), The Analysis of Linear Partial Differential Operators I: Distribution Theory and Fourier Analysis, Classics in Mathematics (2nd ed.), Springer, ISBN 9783642614972