Print Gallery (M. C. Escher)

Print Gallery (Dutch: Prentententoonstelling) is a lithograph printed in 1956 by the Dutch artist M. C. Escher. It depicts a man in a gallery viewing a print of a seaport, and among the buildings in the seaport is the very gallery in which he is standing, making use of the Droste effect with visual recursion.[1] The lithograph has attracted discussion in both mathematical and artistic contexts. Escher considered Print Gallery to be among the best of his works.[2]

Lithograph Print Gallery by M. C. Escher, 1956

Origins

Bruno Ernst cites M. C. Escher as stating that he began Print Gallery "from the idea that it must be possible to make an annular bulge, a cyclic expansion ... without beginning or end."[3] Escher attempted to do this with straight lines, but intuitively switched to using curved lines which make the grid expand greatly as it rotates.[3][4]

Seeming paradox
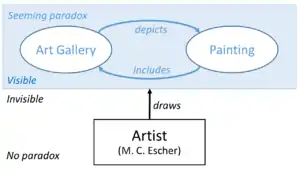
Diagram of the apparent paradox embodied in M. C. Escher's 1956 lithograph Print Gallery, as discussed by Douglas Hofstadter in his 1980 book Gödel, Escher, Bach
Further information: Mathematics and art § Illustrating mathematics

In his book Gödel, Escher, Bach, Douglas Hofstadter explains the seeming paradox embodied in Print Gallery as a strange loop showing three kinds of "in-ness": the gallery is physically in the town ("inclusion"); the town is artistically in the picture ("depiction"); the picture is mentally in the person ("representation").[5]

Possible Droste effect
Further information: Droste effect

Escher's signature is on a circular void in the center of the work. In 2003, two Dutch mathematicians, Bart de Smit and Hendrik Lenstra, reported a way of filling in the void by treating the work as drawn on an elliptic curve over the field of complex numbers. They deem an idealized version of Print Gallery to contain a copy of itself (the Droste effect), rotated clockwise by about 157.63 degrees and shrunk by a factor of about 22.58.[4] Their website further explores the mathematical structure of the picture.[6]

Post-modernism

Print Gallery has been discussed in relation to post-modernism by a number of writers, including Silvio Gaggi,[7] Barbara Freedman,[8] Stephen Bretzius,[9] and Marie-Laure Ryan.[10]

References
  1. Merow, Katharine (2013). "Escher and the Droste Effect". Mathematical Association of America. Archived from the original on 2 August 2013.
  2. Locher, J.L. The Magic of M.C. Escher. Harry N. Abrams, p. 133.
  3. Ernst, Bruno. De toverspiegel van M. C. Escher, Meulenhoff, Amsterdam, 1976; English translation by John E. Brigham: The Magic Mirror of M. C. Escher, Ballantine Books, New York, 1976
  4. de Smit, B.; Lenstra, H. W. (2003). "The Mathematical Structure of Escher's Print Gallery". Notices of the American Mathematical Society. 50 (4): 446–451.
  5. Cooper, Jonathan (5 September 2007). "Art and Mathematics". Retrieved 5 September 2015.
  6. Lenstra, Hendrik; De Smit, Bart. "Applying mathematics to Escher's Print Gallery". Leiden University. Archived from the original on 2018-06-06. Retrieved 6 June 2018.
  7. Gaggi, Silvio (1989). Modern/Postmodern: A Study in Twentieth-Century Arts and Ideas. University of Pennsylvania Press. pp. 44–45. ISBN 0-8122-8154-3.
  8. Freedman, Barbara (1991). Staging the gaze: postmodernism, psychoanalysis, and Shakespearean comedy. Cornell University Press. pp. 124–126. ISBN 0-8014-9737-X.
  9. Bretzius, Stephen (1997). Shakespeare in theory: the postmodern academy and the early modern theater. University of Michigan Press. p. 57. ISBN 0-472-10853-0.
  10. Ryan, Marie-Laure (2000). Narrative as virtual reality: immersion and interactivity in literature and electronic media. Johns Hopkins University Press. p. 165. ISBN 0-8018-6487-9.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.