1729 (number)

1729 is the natural number following 1728 and preceding 1730. It is notably the first taxicab number.

← 1728 1729 1730 →
Cardinalone thousand seven hundred twenty-nine
Ordinal1729th
(one thousand seven hundred twenty-ninth)
Factorization7 × 13 × 19
Divisors1, 7, 13, 19, 91, 133, 247, 1729
Greek numeral,ΑΨΚΘ´
Roman numeralMDCCXXIX
Binary110110000012
Ternary21010013
Senary120016
Octal33018
Duodecimal100112
Hexadecimal6C116

In mathematics
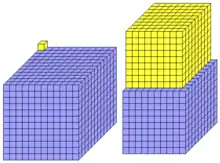
1729 as the sum of two positive cubes.

1729 is the smallest taxicab number,[1] and is variously known as Ramanujan's number or the Ramanujan–Hardy number, after an anecdote of the British mathematician G. H. Hardy when he visited Indian mathematician Srinivasa Ramanujan in hospital. He related their conversation:[2][3][4][5]

I remember once going to see him when he was ill at Putney. I had ridden in taxi cab number 1729 and remarked that the number seemed to me rather a dull one, and that I hoped it was not an unfavourable omen. "No," he replied, "it is a very interesting number; it is the smallest number expressible as the sum of two cubes in two different ways."

The two different ways are:

1729 = 13 + 123 = 93 + 103

The quotation is sometimes expressed using the term "positive cubes", since allowing negative perfect cubes (the cube of a negative integer) gives the smallest solution as 91 (which is a divisor of 1729; 19 × 91 = 1729).

91 = 63 + (−5)3 = 43 + 33

1729 was also found in one of Ramanujan's notebooks dated years before the incident, and was noted by Frénicle de Bessy in 1657. A commemorative plaque now appears at the site of the Ramanujan-Hardy incident, at 2 Colinette Road in Putney.[6]

The same expression defines 1729 as the first in the sequence of "Fermat near misses" defined, in reference to Fermat's Last Theorem, as numbers of the form 1 + z3 which are also expressible as the sum of two other cubes (sequence A050794 in the OEIS).

Other properties

1729 is a sphenic number. It is the third Carmichael number, the first Chernick–Carmichael number (sequence A033502 in the OEIS), the first absolute Euler pseudoprime, and the third Zeisel number.[7] It is a centered cube number,[8] as well as a dodecagonal number,[9] a 24-gonal[10] and 84-gonal number.

Investigating pairs of distinct integer-valued quadratic forms that represent every integer the same number of times, Schiemann found that such quadratic forms must be in four or more variables, and the least possible discriminant of a four-variable pair is 1729.[11]

1729 is the lowest number which can be represented by a Loeschian quadratic form in four different ways with a and b positive integers. The integer pairs are (25,23), (32,15), (37,8) and (40,3).[12]

1729 is also the smallest integer side of an equilateral triangle for which there are three sets of non-equivalent points at integer distances from their vertices: {211, 1541, 1560}, {195, 1544, 1591}, and {824, 915, 1591}.[13]

1729 is the dimension of the Fourier transform on which the fastest known algorithm for multiplying two numbers is based.[14] This is an example of a galactic algorithm.

See also

References
  1. Higgins, Peter (2008). Number Story: From Counting to Cryptography. New York: Copernicus. p. 13. ISBN 978-1-84800-000-1.
  2. Quotations by Hardy Archived 2012-07-16 at the Wayback Machine
  3. Singh, Simon (15 October 2013). "Why is the number 1,729 hidden in Futurama episodes?". BBC News Online. Retrieved 15 October 2013.
  4. Hardy, G H (1940). Ramanujan. New York: Cambridge University Press (original). p. 12.
  5. Hardy, G. H. (1921), "Srinivasa Ramanujan", Proc. London Math. Soc., s2-19 (1): xl–lviii, doi:10.1112/plms/s2-19.1.1-u The anecdote about 1729 occurs on pages lvii and lviii
  6. Marshall, Michael (24 February 2017). "A black plaque for Ramanujan, Hardy and 1,729". Good Thinking. Retrieved 7 March 2019.
  7. Sloane, N. J. A. (ed.). "Sequence A051015 (Zeisel numbers)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-02.
  8. Sloane, N. J. A. (ed.). "Sequence A005898 (Centered cube numbers)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-02.
  9. Sloane, N. J. A. (ed.). "Sequence A051624 (12-gonal (or dodecagonal) numbers)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-02.
  10. Sloane, N. J. A. (ed.). "Sequence A051876 (24-gonal numbers)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-02.
  11. Guy, Richard K. (2004), Unsolved Problems in Number Theory, Problem Books in Mathematics, Volume 1 (3rd ed.), Springer, ISBN 0-387-20860-7 - D1 mentions the Ramanujan-Hardy number.
  12. David Mitchell (25 February 2017). "Tessellating the Ramanujan-Hardy Taxicab Number, 1729, Bedrock of Integer Sequence A198775". Retrieved 19 July 2018.
  13. Ignacio Larrosa Cañestro (June 2016). "Distancias a los vértices de un triángulo equilátero (Distances to vertices of an equilateral triangle)" (PDF) (in Spanish). p. 5.
  14. Harvey, David; Conversation, The. "We've found a quicker way to multiply really big numbers". phys.org. Retrieved 2021-11-01.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.