Types of artificial neural networks
There are many types of artificial neural networks (ANN).
Artificial neural networks are computational models inspired by biological neural networks, and are used to approximate functions that are generally unknown. Particularly, they are inspired by the behaviour of neurons and the electrical signals they convey between input (such as from the eyes or nerve endings in the hand), processing, and output from the brain (such as reacting to light, touch, or heat). The way neurons semantically communicate is an area of ongoing research.[1][2][3][4] Most artificial neural networks bear only some resemblance to their more complex biological counterparts, but are very effective at their intended tasks (e.g. classification or segmentation).
Some artificial neural networks are adaptive systems and are used for example to model populations and environments, which constantly change.
Neural networks can be hardware- (neurons are represented by physical components) or software-based (computer models), and can use a variety of topologies and learning algorithms.
Feedforward
The feedforward neural network was the first and simplest type. In this network the information moves only from the input layer directly through any hidden layers to the output layer without cycles/loops. Feedforward networks can be constructed with various types of units, such as binary McCulloch–Pitts neurons, the simplest of which is the perceptron. Continuous neurons, frequently with sigmoidal activation, are used in the context of backpropagation.
Group method of data handling
The Group Method of Data Handling (GMDH)[5] features fully automatic structural and parametric model optimization. The node activation functions are Kolmogorov–Gabor polynomials that permit additions and multiplications. It uses a deep multilayer perceptron with eight layers.[6] It is a supervised learning network that grows layer by layer, where each layer is trained by regression analysis. Useless items are detected using a validation set, and pruned through regularization. The size and depth of the resulting network depends on the task.[7]
Autoencoder
An autoencoder, autoassociator or Diabolo network[8]: 19 is similar to the multilayer perceptron (MLP) – with an input layer, an output layer and one or more hidden layers connecting them. However, the output layer has the same number of units as the input layer. Its purpose is to reconstruct its own inputs (instead of emitting a target value). Therefore, autoencoders are unsupervised learning models. An autoencoder is used for unsupervised learning of efficient codings,[9][10] typically for the purpose of dimensionality reduction and for learning generative models of data.[11][12]
Probabilistic
A probabilistic neural network (PNN) is a four-layer feedforward neural network. The layers are Input, hidden pattern/summation, and output. In the PNN algorithm, the parent probability distribution function (PDF) of each class is approximated by a Parzen window and a non-parametric function. Then, using PDF of each class, the class probability of a new input is estimated and Bayes’ rule is employed to allocate it to the class with the highest posterior probability.[13] It was derived from the Bayesian network[14] and a statistical algorithm called Kernel Fisher discriminant analysis.[15] It is used for classification and pattern recognition.
Time delay
A time delay neural network (TDNN) is a feedforward architecture for sequential data that recognizes features independent of sequence position. In order to achieve time-shift invariance, delays are added to the input so that multiple data points (points in time) are analyzed together.
It usually forms part of a larger pattern recognition system. It has been implemented using a perceptron network whose connection weights were trained with back propagation (supervised learning).[16]
Convolutional
A convolutional neural network (CNN, or ConvNet or shift invariant or space invariant) is a class of deep network, composed of one or more convolutional layers with fully connected layers (matching those in typical ANNs) on top.[17][18] It uses tied weights and pooling layers. In particular, max-pooling.[19] It is often structured via Fukushima's convolutional architecture.[20] They are variations of multilayer perceptrons that use minimal preprocessing.[21] This architecture allows CNNs to take advantage of the 2D structure of input data.
Its unit connectivity pattern is inspired by the organization of the visual cortex. Units respond to stimuli in a restricted region of space known as the receptive field. Receptive fields partially overlap, over-covering the entire visual field. Unit response can be approximated mathematically by a convolution operation.[22]
CNNs are suitable for processing visual and other two-dimensional data.[23][24] They have shown superior results in both image and speech applications. They can be trained with standard backpropagation. CNNs are easier to train than other regular, deep, feed-forward neural networks and have many fewer parameters to estimate.[25]
Capsule Neural Networks (CapsNet) add structures called capsules to a CNN and reuse output from several capsules to form more stable (with respect to various perturbations) representations.[26]
Examples of applications in computer vision include DeepDream[27] and robot navigation.[28] They have wide applications in image and video recognition, recommender systems[29] and natural language processing.[30]
Deep stacking network
A deep stacking network (DSN)[31] (deep convex network) is based on a hierarchy of blocks of simplified neural network modules. It was introduced in 2011 by Deng and Dong.[32] It formulates the learning as a convex optimization problem with a closed-form solution, emphasizing the mechanism's similarity to stacked generalization.[33] Each DSN block is a simple module that is easy to train by itself in a supervised fashion without backpropagation for the entire blocks.[34]
Each block consists of a simplified multi-layer perceptron (MLP) with a single hidden layer. The hidden layer h has logistic sigmoidal units, and the output layer has linear units. Connections between these layers are represented by weight matrix U; input-to-hidden-layer connections have weight matrix W. Target vectors t form the columns of matrix T, and the input data vectors x form the columns of matrix X. The matrix of hidden units is . Modules are trained in order, so lower-layer weights W are known at each stage. The function performs the element-wise logistic sigmoid operation. Each block estimates the same final label class y, and its estimate is concatenated with original input X to form the expanded input for the next block. Thus, the input to the first block contains the original data only, while downstream blocks' input adds the output of preceding blocks. Then learning the upper-layer weight matrix U given other weights in the network can be formulated as a convex optimization problem:
which has a closed-form solution.[31]
Unlike other deep architectures, such as DBNs, the goal is not to discover the transformed feature representation. The structure of the hierarchy of this kind of architecture makes parallel learning straightforward, as a batch-mode optimization problem. In purely discriminative tasks, DSNs outperform conventional DBNs.
Tensor deep stacking networks
This architecture is a DSN extension. It offers two important improvements: it uses higher-order information from covariance statistics, and it transforms the non-convex problem of a lower-layer to a convex sub-problem of an upper-layer.[35] TDSNs use covariance statistics in a bilinear mapping from each of two distinct sets of hidden units in the same layer to predictions, via a third-order tensor.
While parallelization and scalability are not considered seriously in conventional DNNs,[36][37][38] all learning for DSNs and TDSNs is done in batch mode, to allow parallelization.[39][40] Parallelization allows scaling the design to larger (deeper) architectures and data sets.
The basic architecture is suitable for diverse tasks such as classification and regression.
Regulatory feedback
Regulatory feedback networks started as a model to explain brain phenomena found during recognition including network-wide bursting and difficulty with similarity found universally in sensory recognition. A mechanism to perform optimization during recognition is created using inhibitory feedback connections back to the same inputs that activate them. This reduces requirements during learning and allows learning and updating to be easier while still being able to perform complex recognition.
A regulatory feedback network makes inferences using negative feedback.[41] The feedback is used to find the optimal activation of units. It is most similar to a non-parametric method but is different from K-nearest neighbor in that it mathematically emulates feedforward networks.
Radial basis function (RBF)
Radial basis functions are functions that have a distance criterion with respect to a center. Radial basis functions have been applied as a replacement for the sigmoidal hidden layer transfer characteristic in multi-layer perceptrons. RBF networks have two layers: In the first, input is mapped onto each RBF in the 'hidden' layer. The RBF chosen is usually a Gaussian. In regression problems the output layer is a linear combination of hidden layer values representing mean predicted output. The interpretation of this output layer value is the same as a regression model in statistics. In classification problems the output layer is typically a sigmoid function of a linear combination of hidden layer values, representing a posterior probability. Performance in both cases is often improved by shrinkage techniques, known as ridge regression in classical statistics. This corresponds to a prior belief in small parameter values (and therefore smooth output functions) in a Bayesian framework.
RBF networks have the advantage of avoiding local minima in the same way as multi-layer perceptrons. This is because the only parameters that are adjusted in the learning process are the linear mapping from hidden layer to output layer. Linearity ensures that the error surface is quadratic and therefore has a single easily found minimum. In regression problems this can be found in one matrix operation. In classification problems the fixed non-linearity introduced by the sigmoid output function is most efficiently dealt with using iteratively re-weighted least squares.
RBF networks have the disadvantage of requiring good coverage of the input space by radial basis functions. RBF centres are determined with reference to the distribution of the input data, but without reference to the prediction task. As a result, representational resources may be wasted on areas of the input space that are irrelevant to the task. A common solution is to associate each data point with its own centre, although this can expand the linear system to be solved in the final layer and requires shrinkage techniques to avoid overfitting.
Associating each input datum with an RBF leads naturally to kernel methods such as support vector machines (SVM) and Gaussian processes (the RBF is the kernel function). All three approaches use a non-linear kernel function to project the input data into a space where the learning problem can be solved using a linear model. Like Gaussian processes, and unlike SVMs, RBF networks are typically trained in a maximum likelihood framework by maximizing the probability (minimizing the error). SVMs avoid overfitting by maximizing instead a margin. SVMs outperform RBF networks in most classification applications. In regression applications they can be competitive when the dimensionality of the input space is relatively small.
How RBF networks work
RBF neural networks are conceptually similar to K-Nearest Neighbor (k-NN) models. The basic idea is that similar inputs produce similar outputs.
Assume that each case in a training set has two predictor variables, x and y, and the target variable has two categories, positive and negative. Given a new case with predictor values x=6, y=5.1, how is the target variable computed?
The nearest neighbor classification performed for this example depends on how many neighboring points are considered. If 1-NN is used and the closest point is negative, then the new point should be classified as negative. Alternatively, if 9-NN classification is used and the closest 9 points are considered, then the effect of the surrounding 8 positive points may outweigh the closest 9-th (negative) point.
An RBF network positions neurons in the space described by the predictor variables (x,y in this example). This space has as many dimensions as predictor variables. The Euclidean distance is computed from the new point to the center of each neuron, and a radial basis function (RBF, also called a kernel function) is applied to the distance to compute the weight (influence) for each neuron. The radial basis function is so named because the radius distance is the argument to the function.
- Weight = RBF(distance)
Radial Basis Function
The value for the new point is found by summing the output values of the RBF functions multiplied by weights computed for each neuron.
The radial basis function for a neuron has a center and a radius (also called a spread). The radius may be different for each neuron, and, in RBF networks generated by DTREG, the radius may be different in each dimension.
With larger spread, neurons at a distance from a point have a greater influence.
Architecture
RBF networks have three layers:
- Input layer: One neuron appears in the input layer for each predictor variable. In the case of categorical variables, N-1 neurons are used where N is the number of categories. The input neurons standardizes the value ranges by subtracting the median and dividing by the interquartile range. The input neurons then feed the values to each of the neurons in the hidden layer.
- Hidden layer: This layer has a variable number of neurons (determined by the training process). Each neuron consists of a radial basis function centered on a point with as many dimensions as predictor variables. The spread (radius) of the RBF function may be different for each dimension. The centers and spreads are determined by training. When presented with the x vector of input values from the input layer, a hidden neuron computes the Euclidean distance of the test case from the neuron's center point and then applies the RBF kernel function to this distance using the spread values. The resulting value is passed to the summation layer.
- Summation layer: The value coming out of a neuron in the hidden layer is multiplied by a weight associated with the neuron and adds to the weighted values of other neurons. This sum becomes the output. For classification problems, one output is produced (with a separate set of weights and summation unit) for each target category. The value output for a category is the probability that the case being evaluated has that category.
Training
The following parameters are determined by the training process:
- The number of neurons in the hidden layer
- The coordinates of the center of each hidden-layer RBF function
- The radius (spread) of each RBF function in each dimension
- The weights applied to the RBF function outputs as they pass to the summation layer
Various methods have been used to train RBF networks. One approach first uses K-means clustering to find cluster centers which are then used as the centers for the RBF functions. However, K-means clustering is computationally intensive and it often does not generate the optimal number of centers. Another approach is to use a random subset of the training points as the centers.
DTREG uses a training algorithm that uses an evolutionary approach to determine the optimal center points and spreads for each neuron. It determines when to stop adding neurons to the network by monitoring the estimated leave-one-out (LOO) error and terminating when the LOO error begins to increase because of overfitting.
The computation of the optimal weights between the neurons in the hidden layer and the summation layer is done using ridge regression. An iterative procedure computes the optimal regularization Lambda parameter that minimizes the generalized cross-validation (GCV) error.
General regression neural network
A GRNN is an associative memory neural network that is similar to the probabilistic neural network but it is used for regression and approximation rather than classification.
Deep belief network
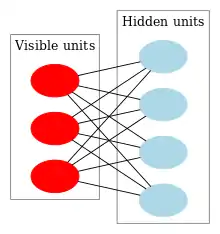
A deep belief network (DBN) is a probabilistic, generative model made up of multiple hidden layers. It can be considered a composition of simple learning modules.[42]
A DBN can be used to generatively pre-train a deep neural network (DNN) by using the learned DBN weights as the initial DNN weights. Various discriminative algorithms can then tune these weights. This is particularly helpful when training data are limited, because poorly initialized weights can significantly hinder learning. These pre-trained weights end up in a region of the weight space that is closer to the optimal weights than random choices. This allows for both improved modeling and faster ultimate convergence.[43]
Recurrent neural network
Recurrent neural networks (RNN) propagate data forward, but also backwards, from later processing stages to earlier stages. RNN can be used as general sequence processors.
Fully recurrent
This architecture was developed in the 1980s. Its network creates a directed connection between every pair of units. Each has a time-varying, real-valued (more than just zero or one) activation (output). Each connection has a modifiable real-valued weight. Some of the nodes are called labeled nodes, some output nodes, the rest hidden nodes.
For supervised learning in discrete time settings, training sequences of real-valued input vectors become sequences of activations of the input nodes, one input vector at a time. At each time step, each non-input unit computes its current activation as a nonlinear function of the weighted sum of the activations of all units from which it receives connections. The system can explicitly activate (independent of incoming signals) some output units at certain time steps. For example, if the input sequence is a speech signal corresponding to a spoken digit, the final target output at the end of the sequence may be a label classifying the digit. For each sequence, its error is the sum of the deviations of all activations computed by the network from the corresponding target signals. For a training set of numerous sequences, the total error is the sum of the errors of all individual sequences.
To minimize total error, gradient descent can be used to change each weight in proportion to its derivative with respect to the error, provided the non-linear activation functions are differentiable. The standard method is called "backpropagation through time" or BPTT, a generalization of back-propagation for feedforward networks.[44][45] A more computationally expensive online variant is called "Real-Time Recurrent Learning" or RTRL.[46][47] Unlike BPTT this algorithm is local in time but not local in space.[48][49] An online hybrid between BPTT and RTRL with intermediate complexity exists,[50][51] with variants for continuous time.[52] A major problem with gradient descent for standard RNN architectures is that error gradients vanish exponentially quickly with the size of the time lag between important events.[53][54] The Long short-term memory architecture overcomes these problems.[55]
In reinforcement learning settings, no teacher provides target signals. Instead a fitness function or reward function or utility function is occasionally used to evaluate performance, which influences its input stream through output units connected to actuators that affect the environment. Variants of evolutionary computation are often used to optimize the weight matrix.
Hopfield
The Hopfield network (like similar attractor-based networks) is of historic interest although it is not a general RNN, as it is not designed to process sequences of patterns. Instead it requires stationary inputs. It is an RNN in which all connections are symmetric. It guarantees that it will converge. If the connections are trained using Hebbian learning the Hopfield network can perform as robust content-addressable memory, resistant to connection alteration.
Boltzmann machine
The Boltzmann machine can be thought of as a noisy Hopfield network. It is one of the first neural networks to demonstrate learning of latent variables (hidden units). Boltzmann machine learning was at first slow to simulate, but the contrastive divergence algorithm speeds up training for Boltzmann machines and Products of Experts.
Self-organizing map
The self-organizing map (SOM) uses unsupervised learning. A set of neurons learn to map points in an input space to coordinates in an output space. The input space can have different dimensions and topology from the output space, and SOM attempts to preserve these.
Learning vector quantization
Learning vector quantization (LVQ) can be interpreted as a neural network architecture. Prototypical representatives of the classes parameterize, together with an appropriate distance measure, in a distance-based classification scheme.
Simple recurrent
Simple recurrent networks have three layers, with the addition of a set of "context units" in the input layer. These units connect from the hidden layer or the output layer with a fixed weight of one.[56] At each time step, the input is propagated in a standard feedforward fashion, and then a backpropagation-like learning rule is applied (not performing gradient descent). The fixed back connections leave a copy of the previous values of the hidden units in the context units (since they propagate over the connections before the learning rule is applied).
Reservoir computing
Reservoir computing is a computation framework that may be viewed as an extension of neural networks.[57] Typically an input signal is fed into a fixed (random) dynamical system called a reservoir whose dynamics map the input to a higher dimension. A readout mechanism is trained to map the reservoir to the desired output. Training is performed only at the readout stage. Liquid-state machines[58] are a type of reservoir computing.[59]
Echo state
The echo state network (ESN) employs a sparsely connected random hidden layer. The weights of output neurons are the only part of the network that are trained. ESN are good at reproducing certain time series.[60]
Long short-term memory
The long short-term memory (LSTM)[55] avoids the vanishing gradient problem. It works even when with long delays between inputs and can handle signals that mix low and high frequency components. LSTM RNN outperformed other RNN and other sequence learning methods such as HMM in applications such as language learning[61] and connected handwriting recognition.[62]
Bi-directional
Bi-directional RNN, or BRNN, use a finite sequence to predict or label each element of a sequence based on both the past and future context of the element.[63] This is done by adding the outputs of two RNNs: one processing the sequence from left to right, the other one from right to left. The combined outputs are the predictions of the teacher-given target signals. This technique proved to be especially useful when combined with LSTM.[64]
Hierarchical
Hierarchical RNN connects elements in various ways to decompose hierarchical behavior into useful subprograms.[65][66]
Stochastic
A district from conventional neural networks, stochastic artificial neural network used as an approximation to random functions.
Genetic Scale
A RNN (often a LSTM) where a series is decomposed into a number of scales where every scale informs the primary length between two consecutive points. A first order scale consists of a normal RNN, a second order consists of all points separated by two indices and so on. The Nth order RNN connects the first and last node. The outputs from all the various scales are treated as a Committee of Machines and the associated scores are used genetically for the next iteration.
Modular
Biological studies have shown that the human brain operates as a collection of small networks. This realization gave birth to the concept of modular neural networks, in which several small networks cooperate or compete to solve problems.
Committee of machines
A committee of machines (CoM) is a collection of different neural networks that together "vote" on a given example. This generally gives a much better result than individual networks. Because neural networks suffer from local minima, starting with the same architecture and training but using randomly different initial weights often gives vastly different results. A CoM tends to stabilize the result.
The CoM is similar to the general machine learning bagging method, except that the necessary variety of machines in the committee is obtained by training from different starting weights rather than training on different randomly selected subsets of the training data.
Associative
The associative neural network (ASNN) is an extension of committee of machines that combines multiple feedforward neural networks and the k-nearest neighbor technique. It uses the correlation between ensemble responses as a measure of distance amid the analyzed cases for the kNN. This corrects the Bias of the neural network ensemble. An associative neural network has a memory that can coincide with the training set. If new data become available, the network instantly improves its predictive ability and provides data approximation (self-learns) without retraining. Another important feature of ASNN is the possibility to interpret neural network results by analysis of correlations between data cases in the space of models.[67]
Physical
A physical neural network includes electrically adjustable resistance material to simulate artificial synapses. Examples include the ADALINE memristor-based neural network.[68] An optical neural network is a physical implementation of an artificial neural network with optical components.
Dynamic
Dynamic neural networks address nonlinear multivariate behaviour and include (learning of) time-dependent behaviour, such as transient phenomena and delay effects. Techniques to estimate a system process from observed data fall under the general category of system identification.
Cascading
Cascade correlation is an architecture and supervised learning algorithm. Instead of just adjusting the weights in a network of fixed topology,[69] Cascade-Correlation begins with a minimal network, then automatically trains and adds new hidden units one by one, creating a multi-layer structure. Once a new hidden unit has been added to the network, its input-side weights are frozen. This unit then becomes a permanent feature-detector in the network, available for producing outputs or for creating other, more complex feature detectors. The Cascade-Correlation architecture has several advantages: It learns quickly, determines its own size and topology, retains the structures it has built even if the training set changes and requires no backpropagation.
Neuro-fuzzy
A neuro-fuzzy network is a fuzzy inference system in the body of an artificial neural network. Depending on the FIS type, several layers simulate the processes involved in a fuzzy inference-like fuzzification, inference, aggregation and defuzzification. Embedding an FIS in a general structure of an ANN has the benefit of using available ANN training methods to find the parameters of a fuzzy system.
Compositional pattern-producing
Compositional pattern-producing networks (CPPNs) are a variation of artificial neural networks which differ in their set of activation functions and how they are applied. While typical artificial neural networks often contain only sigmoid functions (and sometimes Gaussian functions), CPPNs can include both types of functions and many others. Furthermore, unlike typical artificial neural networks, CPPNs are applied across the entire space of possible inputs so that they can represent a complete image. Since they are compositions of functions, CPPNs in effect encode images at infinite resolution and can be sampled for a particular display at whatever resolution is optimal.
Memory networks
Memory networks[70][71] incorporate long-term memory. The long-term memory can be read and written to, with the goal of using it for prediction. These models have been applied in the context of question answering (QA) where the long-term memory effectively acts as a (dynamic) knowledge base and the output is a textual response.[72]
In sparse distributed memory or hierarchical temporal memory, the patterns encoded by neural networks are used as addresses for content-addressable memory, with "neurons" essentially serving as address encoders and decoders. However, the early controllers of such memories were not differentiable.[73]
One-shot associative memory
This type of network can add new patterns without re-training. It is done by creating a specific memory structure, which assigns each new pattern to an orthogonal plane using adjacently connected hierarchical arrays.[74] The network offers real-time pattern recognition and high scalability; this requires parallel processing and is thus best suited for platforms such as wireless sensor networks, grid computing, and GPGPUs.
Hierarchical temporal memory
Hierarchical temporal memory (HTM) models some of the structural and algorithmic properties of the neocortex. HTM is a biomimetic model based on memory-prediction theory. HTM is a method for discovering and inferring the high-level causes of observed input patterns and sequences, thus building an increasingly complex model of the world.
HTM combines existing ideas to mimic the neocortex with a simple design that provides many capabilities. HTM combines and extends approaches used in Bayesian networks, spatial and temporal clustering algorithms, while using a tree-shaped hierarchy of nodes that is common in neural networks.
Holographic associative memory
Holographic Associative Memory (HAM) is an analog, correlation-based, associative, stimulus-response system. Information is mapped onto the phase orientation of complex numbers. The memory is effective for associative memory tasks, generalization and pattern recognition with changeable attention. Dynamic search localization is central to biological memory. In visual perception, humans focus on specific objects in a pattern. Humans can change focus from object to object without learning. HAM can mimic this ability by creating explicit representations for focus. It uses a bi-modal representation of pattern and a hologram-like complex spherical weight state-space. HAMs are useful for optical realization because the underlying hyper-spherical computations can be implemented with optical computation.[75]
LSTM-related differentiable memory structures
Apart from long short-term memory (LSTM), other approaches also added differentiable memory to recurrent functions. For example:
- Differentiable push and pop actions for alternative memory networks called neural stack machines[76][77]
- Memory networks where the control network's external differentiable storage is in the fast weights of another network[78]
- LSTM forget gates[79]
- Self-referential RNNs with special output units for addressing and rapidly manipulating the RNN's own weights in differentiable fashion (internal storage)[80][81]
- Learning to transduce with unbounded memory[82]
Neural Turing machines
Neural Turing machines (NTM)[83] couple LSTM networks to external memory resources, with which they can interact by attentional processes. The combined system is analogous to a Turing machine but is differentiable end-to-end, allowing it to be efficiently trained by gradient descent. Preliminary results demonstrate that neural Turing machines can infer simple algorithms such as copying, sorting and associative recall from input and output examples.
Differentiable neural computers (DNC) are an NTM extension. They out-performed Neural turing machines, long short-term memory systems and memory networks on sequence-processing tasks.[84][85][86][87][88]
Semantic hashing
Approaches that represent previous experiences directly and use a similar experience to form a local model are often called nearest neighbour or k-nearest neighbors methods.[89] Deep learning is useful in semantic hashing[90] where a deep graphical model the word-count vectors[91] obtained from a large set of documents. Documents are mapped to memory addresses in such a way that semantically similar documents are located at nearby addresses. Documents similar to a query document can then be found by accessing all the addresses that differ by only a few bits from the address of the query document. Unlike sparse distributed memory that operates on 1000-bit addresses, semantic hashing works on 32 or 64-bit addresses found in a conventional computer architecture.
Pointer networks
Deep neural networks can be potentially improved by deepening and parameter reduction, while maintaining trainability. While training extremely deep (e.g., 1 million layers) neural networks might not be practical, CPU-like architectures such as pointer networks[92] and neural random-access machines[93] overcome this limitation by using external random-access memory and other components that typically belong to a computer architecture such as registers, ALU and pointers. Such systems operate on probability distribution vectors stored in memory cells and registers. Thus, the model is fully differentiable and trains end-to-end. The key characteristic of these models is that their depth, the size of their short-term memory, and the number of parameters can be altered independently.
Hybrids
Encoder–decoder networks
Encoder–decoder frameworks are based on neural networks that map highly structured input to highly structured output. The approach arose in the context of machine translation,[94][95][96] where the input and output are written sentences in two natural languages. In that work, an LSTM RNN or CNN was used as an encoder to summarize a source sentence, and the summary was decoded using a conditional RNN language model to produce the translation.[97] These systems share building blocks: gated RNNs and CNNs and trained attention mechanisms.
Other types
Instantaneously trained
Instantaneously trained neural networks (ITNN) were inspired by the phenomenon of short-term learning that seems to occur instantaneously. In these networks the weights of the hidden and the output layers are mapped directly from the training vector data. Ordinarily, they work on binary data, but versions for continuous data that require small additional processing exist.
Spiking
Spiking neural networks (SNN) explicitly consider the timing of inputs. The network input and output are usually represented as a series of spikes (delta function or more complex shapes). SNN can process information in the time domain (signals that vary over time). They are often implemented as recurrent networks. SNN are also a form of pulse computer.[98]
Spiking neural networks with axonal conduction delays exhibit polychronization, and hence could have a very large memory capacity.[99]
SNN and the temporal correlations of neural assemblies in such networks—have been used to model figure/ground separation and region linking in the visual system.
Spatial
Spatial neural networks (SNNs) constitute a supercategory of tailored neural networks (NNs) for representing and predicting geographic phenomena. They generally improve both the statistical accuracy and reliability of the a-spatial/classic NNs whenever they handle geo-spatial datasets, and also of the other spatial (statistical) models (e.g. spatial regression models) whenever the geo-spatial datasets' variables depict non-linear relations.[100][101][102] Examples of SNNs are the OSFA spatial neural networks, SVANNs and GWNNs.
Neocognitron
The neocognitron is a hierarchical, multilayered network that was modeled after the visual cortex. It uses multiple types of units, (originally two, called simple and complex cells), as a cascading model for use in pattern recognition tasks.[103][104][105] Local features are extracted by S-cells whose deformation is tolerated by C-cells. Local features in the input are integrated gradually and classified at higher layers.[106] Among the various kinds of neocognitron[107] are systems that can detect multiple patterns in the same input by using back propagation to achieve selective attention.[108] It has been used for pattern recognition tasks and inspired convolutional neural networks.[109]
Compound hierarchical-deep models
Compound hierarchical-deep models compose deep networks with non-parametric Bayesian models. Features can be learned using deep architectures such as DBNs,[110] deep Boltzmann machines (DBM),[111] deep auto encoders,[112] convolutional variants,[113][114] ssRBMs,[115] deep coding networks,[116] DBNs with sparse feature learning,[117] RNNs,[118] conditional DBNs,[119] denoising autoencoders.[120] This provides a better representation, allowing faster learning and more accurate classification with high-dimensional data. However, these architectures are poor at learning novel classes with few examples, because all network units are involved in representing the input (a distributed representation) and must be adjusted together (high degree of freedom). Limiting the degree of freedom reduces the number of parameters to learn, facilitating learning of new classes from few examples. Hierarchical Bayesian (HB) models allow learning from few examples, for example[121][122][123][124][125] for computer vision, statistics and cognitive science.
Compound HD architectures aim to integrate characteristics of both HB and deep networks. The compound HDP-DBM architecture is a hierarchical Dirichlet process (HDP) as a hierarchical model, incorporating DBM architecture. It is a full generative model, generalized from abstract concepts flowing through the model layers, which is able to synthesize new examples in novel classes that look "reasonably" natural. All the levels are learned jointly by maximizing a joint log-probability score.[126]
In a DBM with three hidden layers, the probability of a visible input ''ν'' is:
where is the set of hidden units, and are the model parameters, representing visible-hidden and hidden-hidden symmetric interaction terms.
A learned DBM model is an undirected model that defines the joint distribution . One way to express what has been learned is the conditional model and a prior term .
Here represents a conditional DBM model, which can be viewed as a two-layer DBM but with bias terms given by the states of :
Deep predictive coding networks
A deep predictive coding network (DPCN) is a predictive coding scheme that uses top-down information to empirically adjust the priors needed for a bottom-up inference procedure by means of a deep, locally connected, generative model. This works by extracting sparse features from time-varying observations using a linear dynamical model. Then, a pooling strategy is used to learn invariant feature representations. These units compose to form a deep architecture and are trained by greedy layer-wise unsupervised learning. The layers constitute a kind of Markov chain such that the states at any layer depend only on the preceding and succeeding layers.
DPCNs predict the representation of the layer, by using a top-down approach using the information in upper layer and temporal dependencies from previous states.[127]
DPCNs can be extended to form a convolutional network.[127]
Multilayer kernel machine
Multilayer kernel machines (MKM) are a way of learning highly nonlinear functions by iterative application of weakly nonlinear kernels. They use kernel principal component analysis (KPCA),[128] as a method for the unsupervised greedy layer-wise pre-training step of deep learning.[129]
Layer learns the representation of the previous layer , extracting the principal component (PC) of the projection layer output in the feature domain induced by the kernel. To reduce the dimensionaliity of the updated representation in each layer, a supervised strategy selects the best informative features among features extracted by KPCA. The process is:
- rank the features according to their mutual information with the class labels;
- for different values of K and , compute the classification error rate of a K-nearest neighbor (K-NN) classifier using only the most informative features on a validation set;
- the value of with which the classifier has reached the lowest error rate determines the number of features to retain.
Some drawbacks accompany the KPCA method for MKMs.
A more straightforward way to use kernel machines for deep learning was developed for spoken language understanding.[130] The main idea is to use a kernel machine to approximate a shallow neural net with an infinite number of hidden units, then use a deep stacking network to splice the output of the kernel machine and the raw input in building the next, higher level of the kernel machine. The number of levels in the deep convex network is a hyper-parameter of the overall system, to be determined by cross validation.
See also
- Adaptive resonance theory
- Artificial life
- Autoassociative memory
- Autoencoder
- Biologically inspired computing
- Blue brain
- Connectionist expert system
- Decision tree
- Expert system
- Genetic algorithm
- In Situ Adaptive Tabulation
- Large memory storage and retrieval neural networks
- Linear discriminant analysis
- Logistic regression
- Multilayer perceptron
- Neural gas
- Neuroevolution, NeuroEvolution of Augmented Topologies (NEAT)
- Ni1000 chip
- Optical neural network
- Particle swarm optimization
- Predictive analytics
- Principal components analysis
- Simulated annealing
- Systolic array
- Time delay neural network (TDNN)
- Graph neural network
References
- University Of Southern California. (2004, June 16). Gray Matters: New Clues Into How Neurons Process Information. ScienceDaily Quote: "... "It's amazing that after a hundred years of modern neuroscience research, we still don't know the basic information processing functions of a neuron," said Bartlett Mel..."
- Weizmann Institute of Science. (2007, April 2). It's Only A Game Of Chance: Leading Theory Of Perception Called Into Question. ScienceDaily Quote: "..."Since the 1980s, many neuroscientists believed they possessed the key for finally beginning to understand the workings of the brain. But we have provided strong evidence to suggest that the brain may not encode information using precise patterns of activity."..."
- University Of California – Los Angeles (2004, December 14). UCLA Neuroscientist Gains Insights Into Human Brain From Study Of Marine Snail. ScienceDaily Quote: "..."Our work implies that the brain mechanisms for forming these kinds of associations might be extremely similar in snails and higher organisms...We don't fully understand even very simple kinds of learning in these animals."..."
- Yale University. (2006, April 13). Brain Communicates In Analog And Digital Modes Simultaneously. ScienceDaily Quote: "...McCormick said future investigations and models of neuronal operation in the brain will need to take into account the mixed analog-digital nature of communication. Only with a thorough understanding of this mixed mode of signal transmission will a truly in depth understanding of the brain and its disorders be achieved, he said..."
- Ivakhnenko, Alexey Grigorevich (1968). "The group method of data handling – a rival of the method of stochastic approximation". Soviet Automatic Control. 13 (3): 43–55.
- Ivakhnenko, A. G. (1971). "Polynomial Theory of Complex Systems". IEEE Transactions on Systems, Man, and Cybernetics. 1 (4): 364–378. doi:10.1109/TSMC.1971.4308320. S2CID 17606980.
- Kondo, T.; Ueno, J. (2008). "Multi-layered GMDH-type neural network self-selecting optimum neural network architecture and its application to 3-dimensional medical image recognition of blood vessels". International Journal of Innovative Computing, Information and Control. 4 (1): 175–187.
- Bengio, Y. (2009). "Learning Deep Architectures for AI" (PDF). Foundations and Trends in Machine Learning. 2: 1–127. CiteSeerX 10.1.1.701.9550. doi:10.1561/2200000006. S2CID 207178999.
- Liou, Cheng-Yuan (2008). "Modeling word perception using the Elman network" (PDF). Neurocomputing. 71 (16–18): 3150–3157. doi:10.1016/j.neucom.2008.04.030.
- Liou, Cheng-Yuan (2014). "Autoencoder for words". Neurocomputing. 139: 84–96. doi:10.1016/j.neucom.2013.09.055.
- Diederik P Kingma; Welling, Max (2013). "Auto-Encoding Variational Bayes". arXiv:1312.6114 [stat.ML].
- Generating Faces with Torch, Boesen A., Larsen L. and Sonderby S.K., 2015 torch
.ch /blog /2015 /11 /13 /gan .html - "Competitive probabilistic neural network (PDF Download Available)". ResearchGate. Retrieved 2017-03-16.
- "Probabilistic Neural Networks". Archived from the original on 2010-12-18. Retrieved 2012-03-22.
- "Archived copy" (PDF). Archived from the original (PDF) on 2012-01-31. Retrieved 2012-03-22.
{{cite web}}: CS1 maint: archived copy as title (link) - TDNN Fundamentals, Kapitel aus dem Online Handbuch des SNNS
- Zhang, Wei (1990). "Parallel distributed processing model with local space-invariant interconnections and its optical architecture". Applied Optics. 29 (32): 4790–7. Bibcode:1990ApOpt..29.4790Z. doi:10.1364/ao.29.004790. PMID 20577468.
- Zhang, Wei (1988). "Shift-invariant pattern recognition neural network and its optical architecture". Proceedings of Annual Conference of the Japan Society of Applied Physics.
- J. Weng, N. Ahuja and T. S. Huang, "Learning recognition and segmentation of 3-D objects from 2-D images," Proc. 4th International Conf. Computer Vision, Berlin, Germany, pp. 121–128, May, 1993.
- Fukushima, K. (1980). "Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position". Biol. Cybern. 36 (4): 193–202. doi:10.1007/bf00344251. PMID 7370364. S2CID 206775608.
- LeCun, Yann. "LeNet-5, convolutional neural networks". Retrieved 16 November 2013.
- "Convolutional Neural Networks (LeNet) – DeepLearning 0.1 documentation". DeepLearning 0.1. LISA Lab. Archived from the original on 28 December 2017. Retrieved 31 August 2013.
- LeCun et al., "Backpropagation Applied to Handwritten Zip Code Recognition," Neural Computation, 1, pp. 541–551, 1989.
- Yann LeCun (2016). Slides on Deep Learning Online
- "Unsupervised Feature Learning and Deep Learning Tutorial". ufldl.stanford.edu.
- Hinton, Geoffrey E.; Krizhevsky, Alex; Wang, Sida D. (2011), "Transforming Auto-Encoders", Artificial Neural Networks and Machine Learning – ICANN 2011, Lecture Notes in Computer Science, vol. 6791, Springer, pp. 44–51, CiteSeerX 10.1.1.220.5099, doi:10.1007/978-3-642-21735-7_6, ISBN 9783642217340, S2CID 6138085
- Szegedy, Christian; Liu, Wei; Jia, Yangqing; Sermanet, Pierre; Reed, Scott E.; Anguelov, Dragomir; Erhan, Dumitru; Vanhoucke, Vincent; Rabinovich, Andrew (2015). "Going deeper with convolutions". IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2015, Boston, MA, USA, June 7–12, 2015. IEEE Computer Society. pp. 1–9. arXiv:1409.4842. doi:10.1109/CVPR.2015.7298594.
- Ran, Lingyan; Zhang, Yanning; Zhang, Qilin; Yang, Tao (2017-06-12). "Convolutional Neural Network-Based Robot Navigation Using Uncalibrated Spherical Images" (PDF). Sensors. 17 (6): 1341. Bibcode:2017Senso..17.1341R. doi:10.3390/s17061341. ISSN 1424-8220. PMC 5492478. PMID 28604624.
- van den Oord, Aaron; Dieleman, Sander; Schrauwen, Benjamin (2013-01-01). Burges, C. J. C.; Bottou, L.; Welling, M.; Ghahramani, Z.; Weinberger, K. Q. (eds.). Deep content-based music recommendation (PDF). Curran Associates. pp. 2643–2651.
- Collobert, Ronan; Weston, Jason (2008-01-01). "A unified architecture for natural language processing". Proceedings of the 25th international conference on Machine learning - ICML '08. New York, NY, USA: ACM. pp. 160–167. doi:10.1145/1390156.1390177. ISBN 978-1-60558-205-4. S2CID 2617020.
- Deng, Li; Yu, Dong; Platt, John (2012). "Scalable stacking and learning for building deep architectures" (PDF). 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). pp. 2133–2136. doi:10.1109/ICASSP.2012.6288333. ISBN 978-1-4673-0046-9. S2CID 16171497.
- Deng, Li; Yu, Dong (2011). "Deep Convex Net: A Scalable Architecture for Speech Pattern Classification" (PDF). Proceedings of the Interspeech: 2285–2288. doi:10.21437/Interspeech.2011-607. S2CID 36439.
- David, Wolpert (1992). "Stacked generalization". Neural Networks. 5 (2): 241–259. CiteSeerX 10.1.1.133.8090. doi:10.1016/S0893-6080(05)80023-1.
- Bengio, Y. (2009-11-15). "Learning Deep Architectures for AI". Foundations and Trends in Machine Learning. 2 (1): 1–127. CiteSeerX 10.1.1.701.9550. doi:10.1561/2200000006. ISSN 1935-8237. S2CID 207178999.
- Hutchinson, Brian; Deng, Li; Yu, Dong (2012). "Tensor deep stacking networks". IEEE Transactions on Pattern Analysis and Machine Intelligence. 1–15 (8): 1944–1957. doi:10.1109/tpami.2012.268. PMID 23267198. S2CID 344385.
- Hinton, Geoffrey; Salakhutdinov, Ruslan (2006). "Reducing the Dimensionality of Data with Neural Networks". Science. 313 (5786): 504–507. Bibcode:2006Sci...313..504H. doi:10.1126/science.1127647. PMID 16873662. S2CID 1658773.
- Dahl, G.; Yu, D.; Deng, L.; Acero, A. (2012). "Context-Dependent Pre-Trained Deep Neural Networks for Large-Vocabulary Speech Recognition". IEEE Transactions on Audio, Speech, and Language Processing. 20 (1): 30–42. CiteSeerX 10.1.1.227.8990. doi:10.1109/tasl.2011.2134090. S2CID 14862572.
- Mohamed, Abdel-rahman; Dahl, George; Hinton, Geoffrey (2012). "Acoustic Modeling Using Deep Belief Networks". IEEE Transactions on Audio, Speech, and Language Processing. 20 (1): 14–22. CiteSeerX 10.1.1.338.2670. doi:10.1109/tasl.2011.2109382. S2CID 9530137.
- Deng, Li; Yu, Dong (2011). "Deep Convex Net: A Scalable Architecture for Speech Pattern Classification" (PDF). Proceedings of the Interspeech: 2285–2288. doi:10.21437/Interspeech.2011-607. S2CID 36439.
- Deng, Li; Yu, Dong; Platt, John (2012). "Scalable stacking and learning for building deep architectures" (PDF). 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). pp. 2133–2136. doi:10.1109/ICASSP.2012.6288333. ISBN 978-1-4673-0046-9. S2CID 16171497.
- Achler T., Omar C., Amir E., "Shedding Weights: More With Less", IEEE Proc. International Joint Conference on Neural Networks, 2008
- Hinton, G.E. (2009). "Deep belief networks". Scholarpedia. 4 (5): 5947. Bibcode:2009SchpJ...4.5947H. doi:10.4249/scholarpedia.5947.
- Larochelle, Hugo; Erhan, Dumitru; Courville, Aaron; Bergstra, James; Bengio, Yoshua (2007). "An empirical evaluation of deep architectures on problems with many factors of variation". Proceedings of the 24th international conference on Machine learning. ICML '07. New York, NY, USA: ACM. pp. 473–480. CiteSeerX 10.1.1.77.3242. doi:10.1145/1273496.1273556. ISBN 9781595937933. S2CID 14805281.
- Werbos, P. J. (1988). "Generalization of backpropagation with application to a recurrent gas market model". Neural Networks. 1 (4): 339–356. doi:10.1016/0893-6080(88)90007-x.
- David E. Rumelhart; Geoffrey E. Hinton; Ronald J. Williams. Learning Internal Representations by Error Propagation.
- A. J. Robinson and F. Fallside. The utility driven dynamic error propagation network. Technical Report CUED/F-INFENG/TR.1, Cambridge University Engineering Department, 1987.
- R. J. Williams and D. Zipser. Gradient-based learning algorithms for recurrent networks and their computational complexity. In Back-propagation: Theory, Architectures and Applications. Hillsdale, NJ: Erlbaum, 1994.
- Schmidhuber, J. (1989). "A local learning algorithm for dynamic feedforward and recurrent networks". Connection Science. 1 (4): 403–412. doi:10.1080/09540098908915650. S2CID 18721007.
- Neural and Adaptive Systems: Fundamentals through Simulation. J.C. Principe, N.R. Euliano, W.C. Lefebvre
- Schmidhuber, J. (1992). "A fixed size storage O(n3) time complexity learning algorithm for fully recurrent continually running networks". Neural Computation. 4 (2): 243–248. doi:10.1162/neco.1992.4.2.243. S2CID 11761172.
- R. J. Williams. Complexity of exact gradient computation algorithms for recurrent neural networks. Technical Report Technical Report NU-CCS-89-27, Boston: Northeastern University, College of Computer Science, 1989.
- Pearlmutter, B. A. (1989). "Learning state space trajectories in recurrent neural networks" (PDF). Neural Computation. 1 (2): 263–269. doi:10.1162/neco.1989.1.2.263. S2CID 16813485.
- S. Hochreiter. Untersuchungen zu dynamischen neuronalen Netzen. Diploma thesis, Institut f. Informatik, Technische Univ. Munich, 1991.
- S. Hochreiter, Y. Bengio, P. Frasconi, and J. Schmidhuber. Gradient flow in recurrent nets: the difficulty of learning long-term dependencies. In S. C. Kremer and J. F. Kolen, editors, A Field Guide to Dynamical Recurrent Neural Networks. IEEE Press, 2001.
- Hochreiter, S.; Schmidhuber, J. (1997). "Long short-term memory". Neural Computation. 9 (8): 1735–1780. doi:10.1162/neco.1997.9.8.1735. PMID 9377276. S2CID 1915014.
- Neural Networks as Cybernetic Systems 2nd and revised edition, Holk Cruse
- Schrauwen, Benjamin, David Verstraeten, and Jan Van Campenhout "An overview of reservoir computing: theory, applications, and implementations." Proceedings of the European Symposium on Artificial Neural Networks ESANN 2007, pp. 471–482.
- Mass, Wolfgang; Nachtschlaeger, T.; Markram, H. (2002). "Real-time computing without stable states: A new framework for neural computation based on perturbations". Neural Computation. 14 (11): 2531–2560. doi:10.1162/089976602760407955. PMID 12433288. S2CID 1045112.
- Echo state network, Scholarpedia
- Jaeger, H.; Harnessing (2004). "Predicting chaotic systems and saving energy in wireless communication". Science. 304 (5667): 78–80. Bibcode:2004Sci...304...78J. CiteSeerX 10.1.1.719.2301. doi:10.1126/science.1091277. PMID 15064413. S2CID 2184251.
- F. A. Gers and J. Schmidhuber. LSTM recurrent networks learn simple context free and context sensitive languages IEEE Transactions on Neural Networks 12(6):1333–1340, 2001.
- A. Graves, J. Schmidhuber. Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks. Advances in Neural Information Processing Systems 22, NIPS'22, p 545-552, Vancouver, MIT Press, 2009.
- Schuster, Mike; Paliwal, Kuldip K. (1997). "Bidirectional recurrent neural networks". IEEE Transactions on Signal Processing. 45 (11): 2673–2681. Bibcode:1997ITSP...45.2673S. CiteSeerX 10.1.1.331.9441. doi:10.1109/78.650093. S2CID 18375389.
- Graves, A.; Schmidhuber, J. (2005). "Framewise phoneme classification with bidirectional LSTM and other neural network architectures". Neural Networks. 18 (5–6): 602–610. CiteSeerX 10.1.1.331.5800. doi:10.1016/j.neunet.2005.06.042. PMID 16112549. S2CID 1856462.
- Schmidhuber, J. (1992). "Learning complex, extended sequences using the principle of history compression". Neural Computation. 4 (2): 234–242. doi:10.1162/neco.1992.4.2.234. S2CID 18271205.
- "Dynamic Representation of Movement Primitives in an Evolved Recurrent Neural Network" (PDF). Archived from the original (PDF) on 2011-07-18. Retrieved 2010-07-12.
- "Associative Neural Network". www.vcclab.org. Retrieved 2017-06-17.
- Anderson, James A.; Rosenfeld, Edward (2000). Talking Nets: An Oral History of Neural Networks. MIT Press. ISBN 9780262511117.
- Fahlman, Scott E.; Lebiere, Christian (August 29, 1991). "The Cascade-Correlation Learning Architecture" (PDF). Carnegie Mellon University. Archived from the original (PDF) on 3 May 2013. Retrieved 4 October 2014.
- Schmidhuber, Juergen (2014). "Memory Networks". arXiv:1410.3916 [cs.AI].
- Schmidhuber, Juergen (2015). "End-To-End Memory Networks". arXiv:1503.08895 [cs.NE].
- Schmidhuber, Juergen (2015). "Large-scale Simple Question Answering with Memory Networks". arXiv:1506.02075 [cs.LG].
- Hinton, Geoffrey E. (1984). "Distributed representations". Archived from the original on 2016-05-02.
- Nasution, B.B.; Khan, A.I. (February 2008). "A Hierarchical Graph Neuron Scheme for Real-Time Pattern Recognition". IEEE Transactions on Neural Networks. 19 (2): 212–229. doi:10.1109/TNN.2007.905857. PMID 18269954. S2CID 17573325.
- Sutherland, John G. (1 January 1990). "A holographic model of memory, learning and expression". International Journal of Neural Systems. 01 (3): 259–267. doi:10.1142/S0129065790000163.
- S. Das, C.L. Giles, G.Z. Sun, "Learning Context Free Grammars: Limitations of a Recurrent Neural Network with an External Stack Memory," Proc. 14th Annual Conf. of the Cog. Sci. Soc., p. 79, 1992.
- Mozer, M. C.; Das, S. (1993). "A connectionist symbol manipulator that discovers the structure of context-free languages". Advances in Neural Information Processing Systems. 5: 863–870. Archived from the original on 2019-12-06. Retrieved 2019-08-25.
- Schmidhuber, J. (1992). "Learning to control fast-weight memories: An alternative to recurrent nets". Neural Computation. 4 (1): 131–139. doi:10.1162/neco.1992.4.1.131. S2CID 16683347.
- Gers, F.; Schraudolph, N.; Schmidhuber, J. (2002). "Learning precise timing with LSTM recurrent networks" (PDF). JMLR. 3: 115–143.
- Jürgen Schmidhuber (1993). "An introspective network that can learn to run its own weight change algorithm". Proceedings of the International Conference on Artificial Neural Networks, Brighton. IEE. pp. 191–195.
- Hochreiter, Sepp; Younger, A. Steven; Conwell, Peter R. (2001). "Learning to Learn Using Gradient Descent". ICANN. 2130: 87–94. CiteSeerX 10.1.1.5.323.
- Schmidhuber, Juergen (2015). "Learning to Transduce with Unbounded Memory". arXiv:1506.02516 [cs.NE].
- Schmidhuber, Juergen (2014). "Neural Turing Machines". arXiv:1410.5401 [cs.NE].
- Burgess, Matt. "DeepMind's AI learned to ride the London Underground using human-like reason and memory". WIRED UK. Retrieved 2016-10-19.
- "DeepMind AI 'Learns' to Navigate London Tube". PCMAG. Retrieved 2016-10-19.
- Mannes, John (13 October 2016). "DeepMind's differentiable neural computer helps you navigate the subway with its memory". TechCrunch. Retrieved 2016-10-19.
- Graves, Alex; Wayne, Greg; Reynolds, Malcolm; Harley, Tim; Danihelka, Ivo; Grabska-Barwińska, Agnieszka; Colmenarejo, Sergio Gómez; Grefenstette, Edward; Ramalho, Tiago (2016-10-12). "Hybrid computing using a neural network with dynamic external memory". Nature. 538 (7626): 471–476. Bibcode:2016Natur.538..471G. doi:10.1038/nature20101. ISSN 1476-4687. PMID 27732574. S2CID 205251479.
- "Differentiable neural computers | DeepMind". DeepMind. Retrieved 2016-10-19.
- Atkeson, Christopher G.; Schaal, Stefan (1995). "Memory-based neural networks for robot learning". Neurocomputing. 9 (3): 243–269. doi:10.1016/0925-2312(95)00033-6.
- Salakhutdinov, Ruslan, and Geoffrey Hinton. "Semantic hashing." International Journal of Approximate Reasoning 50.7 (2009): 969–978.
- Le, Quoc V.; Mikolov, Tomas (2014). "Distributed representations of sentences and documents". arXiv:1405.4053 [cs.CL].
- Schmidhuber, Juergen (2015). "Pointer Networks". arXiv:1506.03134 [stat.ML].
- Schmidhuber, Juergen (2015). "Neural Random-Access Machines". arXiv:1511.06392 [cs.LG].
- Kalchbrenner, N.; Blunsom, P. (2013). Recurrent continuous translation models. EMNLP'2013. pp. 1700–1709.
- Sutskever, I.; Vinyals, O.; Le, Q. V. (2014). "Sequence to sequence learning with neural networks" (PDF). Twenty-eighth Conference on Neural Information Processing Systems. arXiv:1409.3215.
- Schmidhuber, Juergen (2014). "Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation". arXiv:1406.1078 [cs.CL].
- Schmidhuber, Juergen; Courville, Aaron; Bengio, Yoshua (2015). "Describing Multimedia Content using Attention-based Encoder—Decoder Networks". IEEE Transactions on Multimedia. 17 (11): 1875–1886. arXiv:1507.01053. Bibcode:2015arXiv150701053C. doi:10.1109/TMM.2015.2477044. S2CID 1179542.
- Gerstner; Kistler. "Spiking Neuron Models: Single Neurons, Populations, Plasticity". icwww.epfl.ch. Archived from the original on 2017-06-04. Retrieved 2017-06-18. Freely available online textbook
- Izhikevich EM (February 2006). "Polychronization: computation with spikes". Neural Computation. 18 (2): 245–82. doi:10.1162/089976606775093882. PMID 16378515. S2CID 14253998.
- Morer I, Cardillo A, Díaz-Guilera A, Prignano L, Lozano S (2020). "Comparing spatial networks: a one-size-fits-all efficiency-driven approach". Physical Review. 101 (4): 042301. doi:10.1103/PhysRevE.101.042301. hdl:2445/161417. PMID 32422764. S2CID 49564277.
- Gupta J, Molnar C, Xie Y, Knight J, Shekhar S (2021). "Spatial variability aware deep neural networks (SVANN): a general approach". ACM Transactions on Intelligent Systems and Technology. 12 (6): 1–21. doi:10.1145/3466688. S2CID 244786699.
- Hagenauer J, Helbich M (2022). "A geographically weighted artificial neural network". International Journal of Geographical Information Science. 36 (2): 215–235. doi:10.1080/13658816.2021.1871618. S2CID 233883395.
- David H. Hubel and Torsten N. Wiesel (2005). Brain and visual perception: the story of a 25-year collaboration. Oxford University Press. p. 106. ISBN 978-0-19-517618-6.
- Hubel, DH; Wiesel, TN (October 1959). "Receptive fields of single neurones in the cat's striate cortex". J. Physiol. 148 (3): 574–91. doi:10.1113/jphysiol.1959.sp006308. PMC 1363130. PMID 14403679.
- Fukushima 1987, p. 83.
- Fukushima 1987, p. 84.
- Fukushima 2007
- Fukushima 1987, pp.81, 85
- LeCun, Yann; Bengio, Yoshua; Hinton, Geoffrey (2015). "Deep learning". Nature. 521 (7553): 436–444. Bibcode:2015Natur.521..436L. doi:10.1038/nature14539. PMID 26017442. S2CID 3074096.
- Hinton, G. E.; Osindero, S.; Teh, Y. (2006). "A fast learning algorithm for deep belief nets" (PDF). Neural Computation. 18 (7): 1527–1554. CiteSeerX 10.1.1.76.1541. doi:10.1162/neco.2006.18.7.1527. PMID 16764513. S2CID 2309950.
- Hinton, Geoffrey; Salakhutdinov, Ruslan (2009). "Efficient Learning of Deep Boltzmann Machines" (PDF). 3: 448–455. Archived from the original (PDF) on 2015-11-06. Retrieved 2019-08-25.
{{cite journal}}: Cite journal requires|journal=(help) - Larochelle, Hugo; Bengio, Yoshua; Louradour, Jerdme; Lamblin, Pascal (2009). "Exploring Strategies for Training Deep Neural Networks". The Journal of Machine Learning Research. 10: 1–40.
- Coates, Adam; Carpenter, Blake (2011). "Text Detection and Character Recognition in Scene Images with Unsupervised Feature Learning" (PDF): 440–445.
{{cite journal}}: Cite journal requires|journal=(help) - Lee, Honglak; Grosse, Roger (2009). "Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations". Proceedings of the 26th Annual International Conference on Machine Learning. pp. 609–616. CiteSeerX 10.1.1.149.6800. doi:10.1145/1553374.1553453. ISBN 9781605585161. S2CID 12008458.
- Courville, Aaron; Bergstra, James; Bengio, Yoshua (2011). "Unsupervised Models of Images by Spike-and-Slab RBMs" (PDF). Proceedings of the 28th International Conference on Machine Learning. Vol. 10. pp. 1–8. Archived from the original (PDF) on 2016-03-04. Retrieved 2019-08-25.
- Lin, Yuanqing; Zhang, Tong; Zhu, Shenghuo; Yu, Kai (2010). "Deep Coding Network". Advances in Neural Information Processing Systems 23 (NIPS 2010). Vol. 23. pp. 1–9.
- Ranzato, Marc Aurelio; Boureau, Y-Lan (2007). "Sparse Feature Learning for Deep Belief Networks" (PDF). Advances in Neural Information Processing Systems. 23: 1–8. Archived from the original (PDF) on 2016-03-04. Retrieved 2019-08-25.
- Socher, Richard; Lin, Clif (2011). "Parsing Natural Scenes and Natural Language with Recursive Neural Networks" (PDF). Proceedings of the 26th International Conference on Machine Learning. Archived from the original (PDF) on 2016-03-04. Retrieved 2019-08-25.
- Taylor, Graham; Hinton, Geoffrey (2006). "Modeling Human Motion Using Binary Latent Variables" (PDF). Advances in Neural Information Processing Systems. Archived from the original (PDF) on 2016-03-04. Retrieved 2019-08-25.
- Vincent, Pascal; Larochelle, Hugo (2008). "Extracting and composing robust features with denoising autoencoders". Proceedings of the 25th international conference on Machine learning - ICML '08. pp. 1096–1103. CiteSeerX 10.1.1.298.4083. doi:10.1145/1390156.1390294. ISBN 9781605582054. S2CID 207168299.
- Kemp, Charles; Perfors, Amy; Tenenbaum, Joshua (2007). "Learning overhypotheses with hierarchical Bayesian models". Developmental Science. 10 (3): 307–21. CiteSeerX 10.1.1.141.5560. doi:10.1111/j.1467-7687.2007.00585.x. PMID 17444972.
- Xu, Fei; Tenenbaum, Joshua (2007). "Word learning as Bayesian inference". Psychol. Rev. 114 (2): 245–72. CiteSeerX 10.1.1.57.9649. doi:10.1037/0033-295X.114.2.245. PMID 17500627.
- Chen, Bo; Polatkan, Gungor (2011). "The Hierarchical Beta Process for Convolutional Factor Analysis and Deep Learning" (PDF). Proceedings of the 28th International Conference on International Conference on Machine Learning. Omnipress. pp. 361–368. ISBN 978-1-4503-0619-5.
- Fei-Fei, Li; Fergus, Rob (2006). "One-shot learning of object categories". IEEE Transactions on Pattern Analysis and Machine Intelligence. 28 (4): 594–611. CiteSeerX 10.1.1.110.9024. doi:10.1109/TPAMI.2006.79. PMID 16566508. S2CID 6953475.
- Rodriguez, Abel; Dunson, David (2008). "The Nested Dirichlet Process". Journal of the American Statistical Association. 103 (483): 1131–1154. CiteSeerX 10.1.1.70.9873. doi:10.1198/016214508000000553. S2CID 13462201.
- Ruslan, Salakhutdinov; Joshua, Tenenbaum (2012). "Learning with Hierarchical-Deep Models". IEEE Transactions on Pattern Analysis and Machine Intelligence. 35 (8): 1958–71. CiteSeerX 10.1.1.372.909. doi:10.1109/TPAMI.2012.269. PMID 23787346. S2CID 4508400.
- Chalasani, Rakesh; Principe, Jose (2013). "Deep Predictive Coding Networks". arXiv:1301.3541 [cs.LG].
- Scholkopf, B; Smola, Alexander (1998). "Nonlinear component analysis as a kernel eigenvalue problem". Neural Computation. 44 (5): 1299–1319. CiteSeerX 10.1.1.53.8911. doi:10.1162/089976698300017467. S2CID 6674407.
- Cho, Youngmin (2012). "Kernel Methods for Deep Learning" (PDF): 1–9.
{{cite journal}}: Cite journal requires|journal=(help) - Deng, Li; Tur, Gokhan; He, Xiaodong; Hakkani-Tür, Dilek (2012-12-01). "Use of Kernel Deep Convex Networks and End-To-End Learning for Spoken Language Understanding". Microsoft Research.