Rhombicosahedron
In geometry, the rhombicosahedron is a nonconvex uniform polyhedron, indexed as U56. It has 50 faces (30 squares and 20 hexagons), 120 edges and 60 vertices.[1] Its vertex figure is an antiparallelogram.
| Rhombicosahedron | |
|---|---|
 | |
| Type | Uniform star polyhedron |
| Elements | F = 50, E = 120 V = 60 (χ = −10) |
| Faces by sides | 30{4}+20{6} |
| Coxeter diagram |      (with extra double-covered pentagrams) (with extra double-covered pentagons) |
| Wythoff symbol | 2 3 (5/4 5/2) | |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U56, C72, W96 |
| Dual polyhedron | Rhombicosacron |
| Vertex figure | 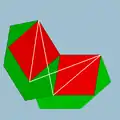 4.6.4/3.6/5 |
| Bowers acronym | Ri |
3D model of a rhombicosahedron
Related polyhedra
A rhombicosahedron shares its vertex arrangement with the uniform compounds of 10 or 20 triangular prisms. It additionally shares its edges with the rhombidodecadodecahedron (having the square faces in common) and the icosidodecadodecahedron (having the hexagonal faces in common).
 Convex hull |
 Rhombidodecadodecahedron |
 Icosidodecadodecahedron |
Rhombicosahedron |
 Compound of ten triangular prisms |
 Compound of twenty triangular prisms |
Rhombicosacron
| Rhombicosacron | |
|---|---|
 | |
| Type | Star polyhedron |
| Face |  |
| Elements | F = 60, E = 120 V = 50 (χ = −10) |
| Symmetry group | Ih, [5,3], *532 |
| Index references | DU56 |
| dual polyhedron | Rhombicosahedron |
3D model of a rhombicosacron
The rhombicosacron is a nonconvex isohedral polyhedron. It is the dual of the uniform rhombicosahedron, U56. It has 50 vertices, 120 edges, and 60 crossed-quadrilateral faces.
References
- Maeder, Roman. "56: rhombicosahedron". MathConsult.
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 0730208
External links
- Weisstein, Eric W. "Rhombicosacron". MathWorld.
- Weisstein, Eric W. "Rhombicosahedron". MathWorld.
- Uniform polyhedra and duals
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.