Rigid origami

Rigid origami is a branch of origami which is concerned with folding structures using flat rigid sheets joined by hinges. That is, unlike in traditional origami, the panels of the paper cannot be bent during the folding process; they must remain flat at all times, and the paper only folded along its hinges. A rigid origami model would still be foldable if it was made from glass sheets with hinges in place of its crease lines.

However, there is no requirement that the structure start as a single flat sheet – for instance shopping bags with flat bottoms are studied as part of rigid origami.

Rigid origami is a part of the study of the mathematics of paper folding, and rigid origami structures can be considered as a type of mechanical linkage. Rigid origami has great practical utility.

Mathematics

The number of standard origami bases that can be folded using rigid origami is restricted by its rules.[1] Rigid origami does not have to follow the Huzita–Hatori axioms, the fold lines can be calculated rather than having to be constructed from existing lines and points. When folding rigid origami flat, Kawasaki's theorem and Maekawa's theorem restrict the folding patterns that are possible, just as they do in conventional origami, but they no longer form an exact characterization: some patterns that can be folded flat in conventional origami cannot be folded flat rigidly.[2]

The Bellows theorem says that a flexible polyhedron has constant volume when flexed rigidly.[3]

The napkin folding problem asks whether it is possible to fold a square so the perimeter of the resulting flat figure is increased. That this can be solved within rigid origami was proved by A.S. Tarasov in 2004.[4]

Blooming is a rigid origami motion of a net of a polyhedron from its flat unfolded state to the folded polyhedron, or vice versa. Although every convex polyhedron has a net with a blooming, it is not known whether there exists a blooming that does not cut across faces of the polyhedron, or whether all nets of convex polyhedra have bloomings.[5]

Complexity theory

Determining whether all creases of a crease pattern can be folded simultaneously as a piece of rigid origami, or whether a subset of the creases can be folded, are both NP-hard. This is true even for determining the existence of a folding motion that keeps the paper arbitrarily close to its flat state, so (unlike for other results in the hardness of folding origami crease patterns) this result does not rely on the impossibility of self-intersections of the folded paper.[6]

Applications
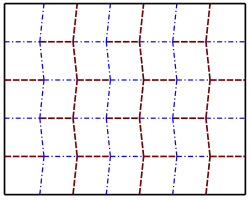
Crease pattern for a Miura fold. The parallelograms of this example have 84° and 96° angles.

The Miura fold is a rigid fold that has been used to pack large solar panel arrays for space satellites, which have to be folded before deployment.

Robert J. Lang has applied rigid origami to the problem of folding a space telescope.[7]

Although paper shopping bags are commonly folded flat and then unfolded open, the standard folding pattern for doing so is not rigid; the sides of the bag bend slightly when it is folded and unfolded. The tension in the paper from this bending causes it to snap into its two flat states, the flat-folded and opened bag.[8]

Recreational uses

Martin Gardner has popularised flexagons which are a form of rigid origami and the flexatube.[9]

Kaleidocycles are toys, usually made of paper, which give an effect similar to a kaleidoscope when convoluted.

References
  1. Demaine, E. D. (2001). Folding and Unfolding. Doctoral Thesis (PDF). University of Waterloo, Canada.{{cite book}}: CS1 maint: location missing publisher (link)
  2. Abel, Zachary; Cantarella, Jason; Demaine, Erik D.; Eppstein, David; Hull, Thomas C.; Ku, Jason S.; Lang, Robert J.; Tachi, Tomohiro (2016). "Rigid origami vertices: conditions and forcing sets". Journal of Computational Geometry. 7 (1): 171–184. doi:10.20382/jocg.v7i1a9. MR 3491092. S2CID 7181079.
  3. Connelly, R.; Sabitov, I.; Walz, A. (1997). "The bellows conjecture". Beiträge zur Algebra und Geometrie. 38 (1): 1–10. MR 1447981.
  4. Tarasov, A. S. (2004). "Solution of Arnold's "folded ruble" problem". Chebyshevskii Sbornik (in Russian). 5 (1): 174–187. Archived from the original on 2007-08-25.
  5. Miller, Ezra; Pak, Igor (2008). "Metric combinatorics of convex polyhedra: Cut loci and nonoverlapping unfoldings". Discrete & Computational Geometry. 39 (1–3): 339–388. doi:10.1007/s00454-008-9052-3. MR 2383765. S2CID 10227925.. Announced in 2003.
  6. Akitaya, Hugo; Demaine, Erik; Horiyama, Takashi; Hull, Thomas; Ku, Jason; Tachi, Tomohiro (2020). "Rigid foldability is NP-hard". Journal of Computational Geometry. 11 (1). arXiv:1812.01160.
  7. "The Eyeglass Space Telescope" (PDF).
  8. Devin. J. Balkcom, Erik D. Demaine, Martin L. Demaine (November 2004). "Folding Paper Shopping Bags". Abstracts from the 14th Annual Fall Workshop on Computational Geometry. Cambridge, Massachusetts: 14–15.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  9. Weisstein, Eric W. "Flexatube". Wolfram MathWorld.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.