Waldhausen category

Let C be a category, co(C) and we(C) two classes of morphisms in C, called cofibrations and weak equivalences respectively. The triple (C, co(C), we(C)) is called a Waldhausen category if it satisfies the following axioms, motivated by the similar properties for the notions of cofibrations and weak homotopy equivalences of topological spaces:

• C has a zero object, denoted by 0;
• isomorphisms are included in both co(C) and we(C);
• co(C) and we(C) are closed under composition;
• for each object A ∈ C the unique map 0 → A is a cofibration, i.e. is an element of co(C);
• co(C) and we(C) are compatible with pushouts in a certain sense.

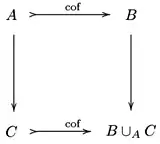
For example, if ${\displaystyle \scriptstyle A\,\rightarrowtail \,B}$ is a cofibration and ${\displaystyle \scriptstyle A\,\to \,C}$ is any map, then there must exist a pushout ${\displaystyle \scriptstyle B\,\cup _{A}\,C}$, and the natural map ${\displaystyle \scriptstyle C\,\rightarrowtail \,B\,\cup _{A}\,C}$ should be cofibration:

In algebraic K-theory and homotopy theory there are several notions of categories equipped with some specified classes of morphisms. If C has a structure of an exact category, then by defining we(C) to be isomorphisms, co(C) to be admissible monomorphisms, one obtains a structure of a Waldhausen category on C. Both kinds of structure may be used to define K-theory of C, using the Q-construction for an exact structure and S-construction for a Waldhausen structure. An important fact is that the resulting K-theory spaces are homotopy equivalent.

If C is a model category with a zero object, then the full subcategory of cofibrant objects in C may be given a Waldhausen structure.

The Waldhausen S-construction produces from a Waldhausen category C a sequence of Kan complexes ${\displaystyle S_{n}(C)}$, which forms a spectrum. Let ${\displaystyle K(C)}$ denote the loop space of the geometric realization ${\displaystyle |S_{*}(C)|}$ of ${\displaystyle S_{*}(C)}$. Then the group

${\displaystyle \pi _{n}K(C)=\pi _{n+1}|S_{*}(C)|}$

is the n-th K-group of C. Thus, it gives a way to define higher K-groups. Another approach for higher K-theory is Quillen's Q-construction.

The construction is due to Friedhelm Waldhausen.

A category C is equipped with bifibrations if it has cofibrations and its opposite category C^OP has so also. In that case, we denote the fibrations of C^OP by quot(C). In that case, C is a biWaldhausen category if C has bifibrations and weak equivalences such that both (C, co(C), we) and (C^OP, quot(C), we^OP) are Waldhausen categories.

Waldhausen and biWaldhausen categories are linked with algebraic K-theory. There, many interesting categories are complicial biWaldhausen categories. For example: The category ${\displaystyle \scriptstyle C^{b}({\mathcal {A}})}$ of bounded chain complexes on an exact category ${\displaystyle \scriptstyle {\mathcal {A}}}$. The category ${\displaystyle \scriptstyle S_{n}{\mathcal {C}}}$ of functors ${\displaystyle \scriptstyle \operatorname {Ar} (\Delta ^{n})\,\to \,{\mathcal {C}}}$ when ${\displaystyle \scriptstyle {\mathcal {C}}}$ is so. And given a diagram ${\displaystyle \scriptstyle I}$, then ${\displaystyle \scriptstyle {\mathcal {C}}^{I}}$ is a nice complicial biWaldhausen category when ${\displaystyle \scriptstyle {\mathcal {C}}}$ is.

• Waldhausen, Friedhelm (1985), "Algebraic K-theory of spaces", Algebraic and geometric topology (New Brunswick, N.J., 1983 (PDF), Lecture Notes in Mathematics, vol. 1126, Berlin: Springer, pp. 318–419, doi:10.1007/BFb0074449, ISBN 978-3-540-15235-4, MR 0802796
• C. Weibel, The K-book, an introduction to algebraic K-theory — http://www.math.rutgers.edu/~weibel/Kbook.html
• G. Garkusha, Systems of Diagram Categories and K-theory — https://arxiv.org/abs/math/0401062
• Sagave, S. (2004). "On the algebraic K-theory of model categories". Journal of Pure and Applied Algebra. 190 (1–3): 329–340. doi:10.1016/j.jpaa.2003.11.002.
• Lurie, Jacob, Higher K-Theory of ∞-Categories (Lecture 16) (PDF)

• Complete Segal space

• "Waldhausen S-construction". nLab.