Semantic System
The Semantic System is based on a microtonal musical scale tuned in just intonation, developed by Alain Daniélou.
For Alain Daniélou the subtleties of the intervals of music of oral traditions cannot be expressed using the equal temperament tuning system of 12 notes per octave, which has been the prevalent system in Western culture for around two centuries. This "artificial" musical scale was developed as a compromise, to standardise musical instruments by reducing the number of notes they could play, but it also reduced the possibilities of expression for both composers and musicians.
« Alain Daniélou draws attention to the fact that a musical culture that adopts a system of equal temperament thereby sacrifices the possibility of expressing all but the most general significations inherent in a musical language. »[1]
After many years spent researching and leading experiments in the world of Indian modal music, Alain Daniélou published a book entitled Sémantique Musicale in which he proposes one of the most elaborated microtonal scales of just intonation.
According to him, the human ear is able to identify and classify pitches by using binary, ternary and quinary frequency ratios as a reference point. This theory gives rise to the unequal division of the octave into 53 notes, with frequency ratios composed solely of products of powers of prime numbers 2, 3 and 5.
Underlying theory
Alain Daniélou and ethnomusicology
Alain Daniélou was an ethnomusicologist[2] who, after studying singing with Charles Panzéra and composition with Max d'Ollone, settled in India. He dedicated his work to the study of Hindu music and religion. Following a long collaboration with the University of Santiniketan in Bengal, Tagore offered him the position of head of the music department, which was in charge of broadcasting the poet’s songs. He settled in Varanasi in 1935, where he was appointed director of the department of musicology of Banaras Hindu University in 1949. He was director of the Adyar Library and Research Centre in Madras from 1954 to 1956. Member of the French Institute of Pondicherry from 1957 to 1958, of the École française d'Extrême-Orient in 1959 and the Unesco International Music Council in 1960, Alain Danielou founded in 1963 an International Institute for Comparative Music Studies first in Berlin, then in Venice in 1969, and was director of both of them.[3]
He also created in 1961 the Unesco Collection of Traditional Music of the World, for which he was responsible for twenty years.[4]
Alongside personalities such as the violinist Yehudi Menuhin and the sitar player Ravi Shankar, to whom he was close,[5][6] he played a decisive role in the recognition of classical Indian music not as traditional folk music, which it had been considered as until then, but as a truly savant art, just as much as Western music.
Reference works
In 1926, at the age of 19, Alain Daniélou received a scholarship for a research trip to Algeria to study Arabic music. During this time he became aware of the limits and, to a certain degree, the aberration of a system that divides the octave into 12 equal semitones,[7][8][9] and does not therefore enable musicians to interpret Arabic music, nor most types of music other than Western music. He took up the cause in the footsteps of a number of illustrious predecessors such as Zarlino, Werckmeister, Mercator, Holder and Helmholtz. His discovery of Indian music a few years later strengthened his commitment to this approach.
He is the author of a number of reference works on the subject. In La Sémantique Musicale he writes : « The human brain immediately classifies factors 2, 3 and 5, and certain of their multiples and products, even quite high ones, yet this mechanism ceases to operate when faced with prime numbers above 5. Each interval of the scale we can consider as "natural" (since it is based on ratios of whole numbers), has its own associated emotion or feeling. »
In other words, these intervals generate an emotional reaction within humans that is not only precise, but apparently universal. Alain Daniélou goes on to say : « The Hindu theory of shruti(s), or intervals, and classes of shrutis(s) and jati(s), assigns a specific expressive content to each interval and organises them into categories that can easily—and only—be explained by the nature of their numerical ratio to the 2-3-5 cycles. »
Moreover, the simpler the fraction ratio of the interval (i.e. the less it contains multiples or products of the prime factors 2, 3 and 5), the greater the "emotional charge" the interval carries.
The work of Alain Daniélou has influenced many composers, including Lou Harrison,[10] as well as other musicologists, such as the Canadian Mieczyslaw Kolinski. In Le chemin du Labyrinthe he writes :« In 1991, the Cervo music festival (near Genoa) awarded me a prize in recognition of my work in the fields of ethnomusicology, philosophy, psychology, psycho-acoustics, linguistics and cybernetics, providing fundamental impetus for new music in the second half of the twentieth century. »[11]
The Semantic system
For the last two centuries, Western musicians have been using imperfect musical intervals: those of the equal temperament of 12 notes per octave. While they have been used in the composition of a considerable amount of music, these intervals were a mathematical compromise that enabled the development of a certain category of acoustic, then electronic instruments, that some feel don't account for the finesse of our perceptual system.
Numerous studies demonstrate that humans possess not only much greater analytical capacities than those needed to simply recognise the twelve equal tempered intervals, but that our perception also integrates many psycho-sensory factors, including the ability to connect timbre and intonation.
Historically, it was the philosopher and mathematician Leibniz who developed, in the 17th century, the theory of "subconscious calculation", according to which music was defined as "the pleasure the human soul experiences from counting without being aware that it is counting".
The Pythagorean Jean-Philippe Rameau followed a similar route when he established a connection between our perception of musical intervals and mathematics, and stated that according to him melody stems from harmony, through which it can "allow us to hear the numerical ratios enshrined within the universe".
More recently, a large number of composers such as Harry Patch, Lou Harrison, Terry Riley, La Monte Young, Ben Johnston, Wendy Carlos, David B. Doty and Robert Rich have employed a variety of microtonal scales in just intonation.
In a similar approach to those of Leibniz and Rameau, Alain Daniélou was deeply invested in the study of musical intervals, having studied Indian music and its subtleties for a large part of his life. He developed a musical scale of 53 notes, only using ratios of the prime factors 2, 3 and 5, which according to Fritz Winckel "shed a whole new light on intervals".
5-limit tuning
The Semantic system includes the notion of 5-limit tuning (or 5-limit just intonation)—which refers to the fact that among all the whole numbers that form its ratios, it only uses only products of prime numbers up to 5 (therefore factors 2, 3 and 5, in keeping with Alain Daniélou's theory concerning our perception of musical intervals).
However, because of their remarkable micro-coincidences, harmonic 7 (there are 14 occurrences of this interval in the S-53 scale) and harmonics 17 and 19, if only to mention these three, are naturally present in various configurations, in particular within the Indian shrutis, and these intervals are therefore also part of the Semantic system.
The 22 Indian shrutis
The 22 shrutis represent the basic set of intervals required to perform of all the Indian modes (or ragas), of both Northern and Southern India. Their frequency ratios are often expressed in the form of fractions of 5-limit tuning, i.e. those that only use prime numbers 2, 3 or 5. Alain Daniélou's just intonation system offers an extension of the 22 Indian shrutis, allowing it to include every one of them.
The syntonic comma
Still known as the pramana shruti, the syntonic comma is the smallest of the intervals that separate the Indian shrutis. Its ratio is 81/80 and the scale of 22 shrutis includes 10 of them. Whilst the comma has been suppressed in the different historical Western temperaments and in our present-day equal temperament, it is of great importance in Indian music, and in all just intonation systems, since it expresses, for each chromatic degree, the subtle emotional polarities of harmonics 3 and 5. These 12 commas are larger than the other commas by around a third of a comma, and are found on the borders of the different chromatic notes of the Semantic-53 scale. In 5-limit tuning, their ratio is complex, measuring 20000 / 19683, or 3125 / 3072. In 7-limit tuning, they can be more simply defined as the septimal comma, with a ratio of 64/63.
Quarter tones
In everyday language, these notes are located between two semitones and they are essentially heard in Arab and Greek music throughout Europe and Eastern countries, in Turkey, Persia, as well as in Africa and in Asia. They were also used in tempered scales by certain European microtonal composers during the 19th century.
In traditional music, quarter tones result above all from more or less equal divisions of minor thirds, fourths or fifths, rather than of semitones themselves. Contrary to what can often be read, there are no quarter tones amongst the Indian shrutis. Their extension in the Semantic scale does however include a significant number of quarter tones, resulting mostly from the product of a comma and a disjunction, i.e. 7 kleismas. Since disjunctions are 12 in number, there are thus 24 of this type, with ratios most commonly of 250/243 in 5-limit tuning, or of 36/25 in 7-limit tuning.
The schisma
The 5-limit just intonation schisma (ratio 32 805 / 32 768) is a micro-coincidence of approximately an eleventh of a comma (1,95372 cent), found for example between different versions of the first shruti (the limma, or chromatic semitone) in certain evening and morning ragas: for instance, it is clear that in the Todi (morning) raga, the harmonic path taken to reach the minor second is that of ratio 256/243, whilst in the harmonic context of the Marva raga (evening), it is 135/128. The Todi harmony is extremely minor, whilst the Marva raga has an extremely major harmony, yet their difference in pitch is, by the standards of current musical practice, insignificant.
Two different notes of the same schisma are considered by Indians as one same shruti, and are played with one same key on each version of the Semantic keyboard. For this reason, in 5-limit tuning, many notes on the Semantic have an undefined ratio between two different possible expressions. For its current interval selections, in-depth studies of the Semantic system have enabled its developers to obtain the utmost precision in its deviations, so that for each of its notes, the ratios proposed are those most coherent with the system as a whole.
The Semantic kleismas
Though never found between two successive notes of the Semantic 53-note scale, the kleisma, a coincidence of around a third of a comma, is nevertheless omnipresent within the Semantic system. The kleisma is the natural difference between the last note of a series of 6 minor thirds 6/5 and the third harmonic of the starting note (i.e. a fifth above the octave). Its ratio in 5-limit is therefore 15 625 / 15 552.
However, there are several simpler ratios for different kleismas of around one third of a comma, that prove more appropriate for dividing the syntonic comma 81/80 into three harmonic intervals: for example the septimal kleisma 225/224, or the 17-limit kleisma 256/255. One relatively simple harmonic division of the syntonic comma 81/80 is for example 16000 : 16065 : 16128 : 16200, which combines three different kleismas: 3213/3200; 256/25; 225/224.
In the Semantic 53-note scale, the kleisma is in reality the difference between a disjunction and a comma, and we invariably find the difference of a kleisma between two intervals comprising the same total number of comma + disjunctions, but different by their number of disjunctions, depending on their position in the scale.
With its perfectly balanced distribution of commas / disjunctions, for the same sum of commas + disjunctions, each interval of the Semantic-53 scale can only have one possible kleismic variation: the Semantic-53 scale interval table[12] indicates the kleismic alternative of each of its intervals, with their ratios in 5-limit and 7-limit versions.
Finally, 41 commas (of 3 kleismas) + 12 disjunctions (of 4 kleismas) separate the 53 notes of the Semantic scale, generating together a total of 105 intervals (not including their schismic variations), which are part of a global structure of 171 kleismas per octave. If we approach them from the angle of whole numbers of kleismas, the 171st of the octave is therefore the simplest logarithmic unit allowing us to measure the intervals of the Semantic system.
Given that the notes of the Semantic scale were generated from a series of fifths (or inversely, a series of fourths), we can determine the kleismic values of each of the intervals of the system by multiplying the value in kleismas of the fourths or the fifths by whole numbers.
A fifth (3/2) comprises 100 kleismas and its octave complement, a fourth (4/3) comprises 71.
Therefore, two fifths, for example, reach beyond the octave by one major tone (9/8), which comprises two times 100 kleismas minus one octave (171 kleismas) = 29 kleismas.
Inversely, 16/9, which is the product of two fourths, comprises two times 71 = 142 kleismas.
The major third (factor 5) of the schismatic temperament used in the Semantic system is the equivalent of a series of 8 4ths: 8 times 71 – 3 times 171 (3 octaves) = 55 kleismas.
A perfect major sixth (5/3) can be obtained by adding a fourth and a major third: 71 + 55 = 126 kleismas, etc.
The values of the Indian shrutis are as follows:
- a syntonic comma (81/80) = 3 kleismas;
- a lagu (25/24) = 10 kleismas;
- a limma (256/243 or 135/128) = 13 kleismas.
In total 10 commas + 5 lagus + 7 limmas = 30 + 50 + 91 = 171 kleismas
The 53 commas
After a first cycle of 12 notes generated by a series of 12 fourths (or symmetrically 12 fifths), the most notable following cycle is a series of 53 fourths (or fifths), which produces a division of the octave into just 2 similar interval sizes, distributed in the most balanced manner (7 limmas and 5 apotomes with 12 notes, 41 commas and 12 disjunctions with 53 notes). Although the dimensions of commas and disjunctions are similar, as Alain Daniélou explained, these two types of commas cannot be confused and the Semantic system cannot therefore be likened to a temperament of 53 equal commas, of which the major thirds and perfect major sixths in particular are much more approximate.
On the Semantic Daniélou-53 screen keyboard with its hexagonal keys, the yellow lines indicate the positions of the disjunctions amongst the commas : crossing this line implies a jump of one disjunction (of 4 kleismas) instead of one comma (of 3 kleismas).
Semantic System tuning
| Number | Note | Ratio | Cents | Interval |
|---|---|---|---|---|
| 0 | C | 1/1 | 0 | Unison |
| 1 | C+ | 81/80 | 21,506 | Pramana shruti, syntonic comma |
| 2 | C++ | 128/125 | 41,059 | Diesis, small quartertone |
| 3 | Db- | 25/24 | 70,672 | 5-limit Lagu |
| 4 | Db | 135/128 | 92,179 | Major limma, 1st shruti |
| 5 | Db+ | 16/15 | 111,731 | Diatonic semitone, apotome |
| 6 | Db++ | 27/25 | 133,238 | Zarlino semitone |
| 7 | D-- | 800/729 | 160,897 | High neutral 2nd, Dlotkot |
| 8 | D- | 10/9 | 182,404 | Minor whole tone |
| 9 | D | 9/8 | 203,910 | Major whole tone, 9th harmonic |
| 10 | D+ | 256/225 | 223,463 | Double apotome |
| 11 | D++ | 144/125 | 244,969 | Low semifourth |
| 12 | Eb- | 75/64 | 274,582 | Low minor third |
| 13 | Eb | 32/27 | 294,135 | 3-limit minor third |
| 14 | Eb+ | 6/5 | 315,641 | 5-limit minor third |
| 15 | Eb++ | 243/200 | 337,148 | Double Zalzal (54/49)^2 |
| 16 | E- | 100/81 | 364,807 | Double minor tone |
| 17 | E | 5/4 | 386,314 | 5th harmonic major third |
| 18 | E+ | 81/64 | 407,820 | 3-limit major third |
| 19 | E++ | 32/25 | 427,373 | Supermajor third, Daghboc |
| 20 | F-- | 125/96 | 456,986 | Hypermajor third |
| 21 | F- | 320/243 | 476,539 | Biseptimal slendroic fourth |
| 22 | F | 4/3 | 498,045 | 3-limit natural fourth |
| 23 | F+ | 27/20 | 519,551 | Fourth + pramana shruti |
| 24 | F++ | 512/375 | 539,104 | Fourth + diesis, Zinith |
| 25 | F#- | 25/18 | 568,717 | Major third + minor tone |
| 26 | F# | 45/32 | 590,224 | Diatonic tritone, 11th shruti |
| 27 | F#+ | 64/45 | 609,776 | High tritone, 12th shruti |
| 28 | F#++ | 36/25 | 631,283 | Double minor third |
| 29 | G-- | 375/256 | 660,896 | Narayana, reverse Zinith |
| 30 | G- | 40/27 | 680,449 | Fifth minus pramana |
| 31 | G | 3/2 | 701,955 | 3rd harmonic perfect fifth |
| 32 | G+ | 243/160 | 723,461 | Fifth plus pramana |
| 33 | G++ | 192/125 | 743,014 | Low trisemifourth |
| 34 | Ab- | 25/16 | 772,627 | Low minor sixth, double 5/4 |
| 35 | Ab | 128/81 | 792,180 | 3-limit minor sixth |
| 36 | Ab+ | 8/5 | 813,686 | 5-limit minor sixth |
| 37 | Ab++ | 81/50 | 835,193 | Double Zalzal |
| 38 | A- | 400/243 | 862,852 | Double Daghboc |
| 39 | A | 5/3 | 884,359 | 5-limit major sixth, 16th shruti |
| 40 | A+ | 27/16 | 905,865 | 3-limit major sixth |
| 41 | A++ | 128/75 | 925,418 | Supermajor sixth |
| 42 | Bb-- | 125/72 | 955,031 | Reverse semifourth |
| 43 | Bb- | 225/128 | 976,537 | Low minor seventh |
| 44 | Bb | 16/9 | 996,090 | 3-limit minor seventh |
| 45 | Bb+ | 9/5 | 1017,596 | 5-limit minor seventh |
| 46 | Bb++ | 729/400 | 1039,103 | Low neutral seventh |
| 47 | B- | 50/27 | 1066,762 | Reverse Zarlino semitone |
| 48 | B | 15/8 | 1088,269 | Major seventh, 15th harmonic |
| 49 | B+ | 256/135 | 1107,821 | High major seventh, 21th shruti |
| 50 | B++ | 48/25 | 1129,328 | Reverse 5-limit Lagu |
| 51 | C-- | 125/64 | 1158,941 | Triple major third |
| 52 | C- | 160/81 | 1178,494 | Octave minus pramana |
| 53 | C | 2/1 | 1200,000 | Octave |
Work of reference
Several instruments were built on Alain Daniélou's request. The system he developed belongs to the family of just intonation scales, also sometimes called "natural" scales. This means that the intervals on which the scale is based are expressed in the form of ratios, composed of whole numbers with regards to both the numerator and the denominator, thus creating harmonic ratios between all the notes of the global system, in this case 53 per octave.
This scale has the particularity of highlighting harmonics 2, 3 and 5, and their combinations. The intervals created by these three factors have, according to Alain Daniélou, the power to generate within the listener certain feelings and emotional reactions that are not only precise but also, apparently, universal. These two specific qualities; bringing together 5-limit tuning just intonation intervals and carrying an expressive content, can be found in the Hindu music theory with its 22 shrutis.
The Martenot–Daniélou keyboard

In 1936, Alain Daniélou worked alongside Maurice Martenot, the famous inventor of the "ondes" that bear his name, with whom he built his first keyboard, which was tuneable and displayed interval frequencies. He patented it the following year.[13] The instrument is on display at the Musée de la Musique in Paris.
The Shruti Venu

A number of years later, during his travels in India, he designed a craft-built instrument in Varanasi in 1942, which involved the use of a considerable number of bicycle wheel spokes.
He then build a series of small bellow harmoniums called Shruti Venu, of which one, built at the University of Visva-Bharati was kept and was restored in 2016 by Klaus Blasquiz.
The S52

In 1967, Alain Daniélou designed a new electronic instrument, the S52. To build it he called on Stefan Kudelski from Lausanne, Switzerland, the inventor and builder of the Nagra, the famous luxury portable tape player.
Kudelski entrusted his son André with the project, a young electronics engineer, and Claude Cellier, electronics engineer and musician. This new instrument, which was based exactly on the system presented in the book Sémantique Musicale was highly elaborated from a technical point of view, and although it had a few shortcomings, it nevertheless enabled Alain Daniélou to advance with his theory inspired from the Indian model, and to test its psychoacoustic applications.
The prototype was presented in Paris in 1980, namely at the UNESCO International Music Council and the IRCAM (Institut de Recherche et Coordination Acoustique/Musique / Research and Acoustic/Music Coordination Institute), and afterwards in Bordeaux, Berlin, Rome, etc.
Christened as "Shiva's organ" by the journalist Jean Chalon, the instrument aroused a great deal of interest not only in the field of microtonal music, but also amongst music-therapy specialists and in non-European music. Sylvano Bussotti, who had until then never included electronic instruments in his works, became highly interested in the project, and wrote a piece for the instrument, which was played by the pianist Mauro Castellano and directed by the conductor Marcello Panni in a work called "La Vergine ispirata".
The Semantic Daniélou-36

It was not until 1993 that the idea of an entirely digital instrument came into being, which went by the name of the "Semantic", christened by the composer Sylvano Bussotti in reference to the Alain Daniélou's work Sémantique Musicale.
On Alain Daniélou's request, it was developed by Michel Geiss, an electronics engineer, musician and specialist in electronic instrument design, who at the time was working with Jean Michel Jarre.
The Semantic, later renamed the Semantic Daniélou-36 to avoid confusion with the 2nd version, the Semantic Daniélou-53, contains as its name indicates 36 intervals. These 36 intervals were the ones Alain Daniélou considered the most essential among the 53 of his scale.
Instead of adapting the widely used MIDI piano keyboard controls, Michel Geiss suggested that they use a button keyboard with accordion-type keys. The first advantage being that this would take up less room, allowing a large number of notes in a small space, which was a considerable advantage for a scale containing 36 notes per octave. Secondly, arranging the notes on a piano-type keyboard would inevitably have evoked the equal tempered scale.
Alain Daniélou validated this option, and Michel Geiss managed the project's development. He entrusted the scale and sound programming work to Christian Braut, computer music specialist and author of the reference book "The Musician's Guide to MIDI".[14] Other collaborators in the project were Jean-Claude Dubois, who developed the operating system, and Philippe Monsire, who conceived the futuristic design of the instrument. The Semantic-36 was delivered a few years later, however Alain Daniélou died on 27 January 1994 without having seen the finalised instrument.
The instrument possesses two button keyboards, taken from the MIDY 20 Cavagnolo (MIDI command keyboards for accordionists). Each of them has 120 keys, which gives the player access to just over 6 octaves, instead of just over 2 octaves for the classic 76-note keyboards. These two keyboards are connected to an electronic sound module, or more precisely, the expander version of the Kurzweil K2000 sampler, the K2000R, reprogrammed in just intonation by Christian Braut, according to Alain Daniélou's Semantic scale.
In 2006, Igor Wakhévitch composed the album "Ahata-Anahata" ("the audible and the inaudible"),[15] which was entirely performed on the Semantic Daniélou-36.
In 2007, for the European tour "Semantic Works", a series of concerts involving the instrument were given in Le Thoronet Abbey,[16] the Teatro Palladium in Rome, the Teatro Fondamente Nuove in Venice and the Maison des Cultures du Monde (World Cultures Institute) in Paris, by Jacques Dudon's Ensemble de Musique Microtonale du Thoronet (Thoronet Microtonal Music Ensemble).
In 2013, Michel Geiss developed a greatly improved version of the Semantic Daniélou-36, while conserving the external appearance of the original instrument. The second version made use of recent developments in the world of electronic music and included internal sound-generating software. This major technological update enhanced the instrument by offering the possibility of producing richer, more varied and more expressive sounds, whilst maintaining remarkably precise tuning (to a thousandth of a cent). The new version also boasted a ribbon controller for fine pitch variations.
The Semantic Daniélou-53
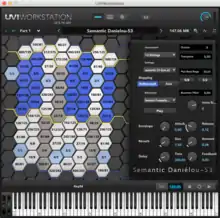
Developed by Christian Braut, Jacques Dudon and Arnaud Sicard (from UVI/Univers Sons), upon request of the FIND Foundation (India-Europe Foundation for New Dialogues), the Semantic Daniélou-53 is the first of the Semantic instruments that integrates the entire Daniélou scale. As its name suggests, it includes 53 intervals and offers 72 scales (or tunings).
Released in 2013, using UVI Workstation technology it is presented in the form of a virtual instrument, which is available for free download for MacOS and Windows.
The Semantic Daniélou-53 can be run on the screen simply by connecting the "hexagonal" keyboard, composed of 74 colour keys (seven columns of 9 keys, one column of 10 keys, the fourth, an extra key on the left), or using MIDI.
Selective bibliography
- Daniélou, Alain (1943). Introduction to the Study of Musical Scales. Benares: A. Bose, Indian Press LTD. ISBN 0-8364-2353-4.
- Daniélou, Alain (1995). Music and the Power of Sound. Rochester, Vermont, USA: Inner Traditions International. ISBN 0-89281-336-9.
- Daniélou, Alain (2003). Traditional Music in Today's World. Varanasi, India: Indica Books. ISBN 8-18656-933-2.
- Daniélou, Alain (1971). The Situation of Music and Musicians in the Countries of the Orient. Firenze: Léo S. Olschki.
- Daniélou, Alain (1968). Northern Indian Music. London: Barrie and Rockliff.
- Daniélou, Alain (1958). "Tableau comparatif des intervalles musicaux". Collection Indologie (in French). Institut français d'indologie. ISSN 0073-8352.
- Daniélou, Alain (1987). Traité de musicologie comparée (in French). Éditions Hermann. ISBN 978-2705612658.
- Daniélou, Alain (2004). Origines et pouvoirs de la musique (in French). Paris, Pondicherry: Kailash Éditions. ISBN 978-2842680909.
- Daniélou, Alain (1978). Sémantique musicale (in French). Éditions Hermann. ISBN 270561334X.
References
- "Sémantique musicale: Essai de psychophysiologie auditive by Alain Daniélou. Review by: Adriaan D. Fokker, Sr., Ethnomusicology, Vol. 13, No. 2 (May, 1969), pp. 371-374". JSTOR 850159.
{{cite journal}}: Cite journal requires|journal=(help) - "Dictionnaire de la musique, Biographie" (in French).
- Pouillon, François (2012). Dictionnaire des orientalistes de langue française, nouvelle édition revue et augmentée, François Pouillon, 1073 pages, éditions Karthala, 2012 (in French). ISBN 9782811107901.
- "UNESCO Collection of Traditional Music of the World".
- "Yehudi Menuhin talks about Alain Daniélou". 10 March 2011.
- "Alain Daniélou The Way to the Labyrinth".
- Small, Christopher (31 July 1998). Musicking: The Meanings of Performing and Listening, Christopher Small, 1998. ISBN 9780819522573.
- Sarath, Edward W. (2 April 2013). Improvisation, Creativity, and Consciousness: Jazz as Integral Template for Music, Education, and Society, by Edward W. Sarath, 2014. ISBN 9781438447230.
- Cox, Christoph; Warner, Daniel (27 July 2017). Audio Culture, Revised Edition: Readings in Modern Music, by Christoph Cox. ISBN 9781501318375.
- Alves, Bill; Campbell, Brett (10 April 2017). American Musical Maverick, Lou Harrison, 2017. ISBN 9780253026439.
- Daniélou, Alain (2015). Le chemin du Labyrinthe. Éditions L'Âge d'Homme. p. 337. ISBN 978-2825143391.
- "Intervals of the Semantic scale".
- "Martenot Daniélou patent". 12 September 2016.
- Braut, Christian (1994). The musician's guide to MIDI, Christian Braut, 1994. ISBN 9780782112856.
- "Igor Wakhévitch official website".
- "Semantic Works, Abbaye du Thoronet, 2007". 16 September 2016.