Slip bands in metals

PSB structure (adopted from [7])

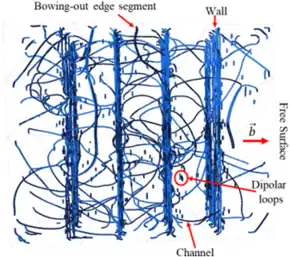
Persistent slip-bands (PSBs) are associated with strain localisation due to fatigue in metals and cracking on the same plane. Transmission electron microscopy (TEM) and three-dimensional discrete dislocation dynamics (DDD[8]) simulation were used to reveal and understand dislocations type and arrangement/patterns to relate it to the sub-surface structure. PSB – ladder structure – is formed mainly from low-density channels of mobile gliding screw dislocation segments and high-density walls of dipolar edge dislocation segments piled up with tangled bowing-out edge segment and different sizes of dipolar loops scattered between the walls and channels.[9][10]

One type of dislocation loop forms the boundary of a completely enclosed patch of slipped material on the slip plane which terminates at the free surface. Widening of the slip band: Screw dislocation can have high enough resolved shear stress for a glide on more than one slip plane. Cross-slip can occur. But this leaves some segments of dislocation on the original slip plane. Dislocation can cross-slip back on to a parallel primary slip plane. where it forms a new dislocation source, and the process can repeat. These walls in PSBs are a ‘dipole dispersion’ form of stable arrangement of edge dislocations with minimal long-range stress field which has a minimal long-range stress field. This is different to slip-bands that is a planar stack of a stable array that has a strong long-range stress field. Thus, – in the free surface – cut and open (elimination) of dislocation loops at the surface cause the irreversible/persistent surface step associated with slip-bands.[10][11][12]

Surface relief through extrusion occurs on the Burger's vector direction and extrusion height and PSB depth increase with PSB thickness.[13] PSB and planar walls are parallel and perpendicularly aligned with the normal direction of the Critical resolved shear stress, respectively.[14] And once dislocation saturate and reach its sessile configuration, cracks were observed to nucleate and propagate along PSB extrusions.[15][16][17] To summarise, contrary to 2D line defects, the field at the slip-band tip is due to three-dimensional interactions where the slip band extrusion simulates a sink-like dislocation blooming along the slip band axis. The magnitude of the gradient deformation field ahead of the slip band depends on the slip height and the mechanical conditions for propagation is influenced by the emitted dislocations long range field.A surface marking, or slip band, appears at the intersection of an active slip plane and the free surface of a crystal. Slip occurs in avalanches separated in time. Avalanches from other slip systems crossing a slip plane containing an active source led to the observed stepped surface markings, with successive avalanches from the given source displaced relative to each other.[18]

Dislocations are generated on a single slip plane They point out that a dislocation segment (Frank–Read source), lying in a slip plane and pinned at both ends, is a source of an unlimited number of dislocation loops. In this way the grouping of dislocations into an avalanche of a thousand or so loops on a single slip plane can be understood.[19] Each dislocation loop has a stress field that opposes the applied stress in the neighbourhood of the source. When enough loops have been generated, the stress at the source will fall to a value so low that additional loops cannot form. Only after the original avalanche of loops has moved some distance away can another avalanche occur.

Generation of the first avalanche at a source is easily understood. When the stress at the source reaches r*, loops are generated, and continue to be generated until the back-stress stops the avalanche. A second avalanche will not occur immediately in polycrystals, for the loops in the first avalanche are stopped or partially stopped at grain boundaries. Only if the external stress is increased substantially will a second avalanche be formed. In this way the formation of additional avalanches with rising stress can be understood.

It remains to explain the displacement of successive avalanches by a small amount normal to the slip plane, thereby accounting for the observed fine structure of slip bands. A displacement of this type requires that a Frank–Read source move relative to the surface where slip bands are observed.

In situ nano-compression work [20] in Transmission electron microscopy (TEM) reveals that the deformation of a-Fe at the nanoscale is an inhomogeneous process characterized by a series of short displacement bursts and intermittent large displacement bursts. The series of short bursts correspond to the collective movement of dislocations within the crystal. The large single bursts are from SBs nucleated from the specimen surface. These results suggest that the formation of SBs can be considered as a source-limited plasticity process. The initial plastic deformation is characterized by the multiplication/ movement of a few dislocations over short distances due to the availability of dislocation sources within the nano-blade. Once it has reached a stage at which the mobile dislocations along preferred slips planes have moved through the nano-blade or become entangled in sessile configurations and further dislocation movement is difficult within the crystal, plasticity is carried out by the formation of SBs, which nucleate from the surface [21] and then propagate through the nano-blade.

Frank–Read source

Fisher et al. [18] proposed that SBs are dynamically generated from a Frank–Read source at the specimen surface and are terminated by their own stress field in single crystals. The displacement burst behaviour reported by Kiener and Minor [22] on compressing Cu single crystal nanopillars. Obviously suppressed the progress of serrated yielding (a series of short strain bursts) relative to that without the spinodal nanostructure. The results revealed that during compression deformation, the spinodal nanostructure confined the movement of dislocations (leading to a significant increase in dislocation density), causing a notable strengthening effect, and also kept the slip band morphology planar.[23]

Dislocation activity assists the growth of austenite precipitates and provide quantitative data for revealing the stress field generated by interface migration.[24] The jerky nature of the tip moving rate is probably due to the accumulation and relaxation of stress field near the tip. After leaving from the tip, the dislocation loop expands rapidly ahead of the tip thus the change in tip velocity is concomitant with dislocation emission. It indicates that the emitted dislocation is strongly repelled by the stress field present at the lath tip. When the loop meets the foil surface, it breaks into two dislocation segments that leave a visible trace, due to the presence of a thin oxide layer on the surface. The emission of a dislocation loop from the tip may also affect tip moving rate via interaction between the local dislocation loop and the possible interfacial dislocations in the semi-coherent interface surrounding the tip. consequently, the tip halted temporarily. The net shear stress acting on each dislocation results from a combination of the stress field at the lath tip (τ_tip), the image stress tending to attract the dislocation loop to the surface (τ_image), the line tension (τ_l) and the interaction stress between dislocations (τ_inter). This implies the strain field due to the transformation of austenite is large enough to cause the nucleation and emission of dislocations from an austenite lath tip.[2]

Slip bands formation

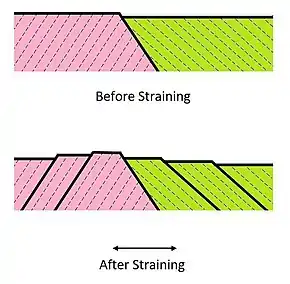
While repeatedly reversed loading commonly leads to localisation of dislocation glide, creating linear extrusions and intrusions on a free surface, similar features can arise even if there is no load reversal. These arise from dislocations gliding on a particular slip plane, in a particular slip direction (within a single grain), under an external load. Steps can be created on the free surface as a consequence of the tendency for dislocations to follow one another along a glide path, of which there may be several in parallel with each other in the grain concerned. Prior passage of dislocations apparently makes glide easier for subsequent ones, and the effect may also be associated with dislocation sources, such as a Frank-Read source, acting in particular planes.

Secondary electron images of age-hardened duplex stainless-steel observed in situ in three-point bending at applied crosshead displacements of (a) 1.2 mm and (b) 1.5 mm. Selected regions (2 and 4) are shown with higher magnification in (c) and (d). The apparent slip band height is marked as ‘h.’ Ferrite (${\displaystyle \alpha }$) and austenite (${\displaystyle \gamma }$) phases are labelled.[1]

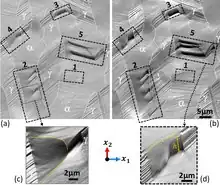
The appearance of such bands, which are sometimes termed “persistent slip lines”, is similar to that of those arising from cyclic loading, but the resultant steps are usually more localised and have lower heights. They also reveal the grain structure. They can often be seen on free surfaces that were polished before the deformation took place. For example, the figure shows micrographs[25] (taken with different magnifications) of the region around an indent created in a copper sample with a spherical indenter. The parallel lines within individual grains are each the result of several hundred dislocations of the same type reaching the free surface, creating steps with a height of the order of a few microns. If a single slip system was operational within a grain, then there is just one set of lines, but it is common for more than one system to be activated within a grain (particularly when the strain is relatively high), leading to two or more sets of parallel lines. Other features indicative of the details of how the plastic deformation took place, such as a region of cooperative shear caused by deformation twinning, can also sometimes be seen on such surfaces. In the optical micrograph shown, there is also evidence of grain rotations – for example, at the “rim” of the indent and in the form of depressions at grain boundaries. Such images can thus be very informative.

Nature of the non-cyclic slip band local field

Schematic of a slip band, relative to the measurement axes (𝑥₁, 𝑥₂, and 𝑥₃), and axes related to the slip-band (𝑥, 𝑦, and 𝑧), showing the angles that describe the relationship between these axes and the traces of the slip band (𝛼, 𝜃), and the inclination angle (𝜓) of the slip trace (𝑥) and Burgers vector (𝑏) relative to the surface. ℎ is the slip band height, and 𝑞 is the slip band propagation direction assumed for J-integral calculation when using the virtual extension method.[26] 𝑡 describes the line vector drawn here as for an edge dislocation, i.e., 𝑏⊥𝑡, and 𝑛 is the slip band plane normal.[1]

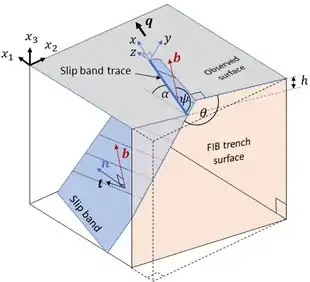
The deformation field at the slip-band is due to three-dimensional elastic and plastic strains where the concentrated shear of the slip band tip deforms the grain in its vicinity. The elastic strains describe the stress concentration ahead of the slip band, which is important as it can affect the transfer of plastic deformation across grain boundaries.[27][28][29] An understanding of this is needed to support the study of yield and inter/intra-granular fracture.[30][31][32] The concentrated shear of slip bands can also nucleate cracks in the plane of the slip band,[16][17] and persistent slip bands that lead to intragranular fatigue crack initiation and growth may also form under cyclic loading conditions.[5][33] To properly characterise slip bands and validate mechanistic models for their interactions with microstructure, it is crucial to quantify the local deformation fields associated with their propagation. However, little attention has been given to slip bands within grains (i.e., in the absence of grain boundary interaction).

The long-range stress field (i.e., the elastic strain field) around the tip of a stress concentrator, such as a slip band,, can be considered a singularity equivalent to that of a crack.[34][35] This singularity can be quantified using a path independent integral since it satisfies the conservation laws of elasticity. The conservation laws of elasticity related to translational, rotational, and scaling symmetries were derived initially by Knowles and Sternberg [36] from the Noether's theorem.[37] Budiansky and Rice[38] introduced the J-, M-, L-integral and were the first to give them a physical interpretation as the strain energy-release rates for mechanisms such as cavity propagation, simultaneous uniform expansion, and defect rotation, respectively. When evaluated over a surface that encloses a defect, these conservation integrals represent a configurational force on the defect.[39] That work paved the way for the field of Configurational mechanics of materials, with the path-independent J-integral now widely used to analyse the configurational forces in problems as diverse as dislocation dynamics,[40][41] misfitting inclusions,[42] propagation of cracks,[43] shear deformation of clays,[44] and co-planar dislocation nucleation from shear loaded cracks.[45] The integrals have been applied to linear elastic and elastic-plastic materials and have been coupled with processes such as thermal [46] and electrochemical [47] loading, and internal tractions.[48] Recently, experimental fracture mechanics studies have used full-field in situ measurements of displacements [49][50] and elastic strains [51][50] to evaluate the local deformation field surrounding the crack tip as a J-integral.

Slip bands form due to plastic deformation, and the analysis of the force on a dislocation considers the two-dimensional nature of the dislocation line defect. General definitions of the Peach–Koehler configurational force (𝑃_𝑘𝑗) [52] (or the elastic energy-momentum tensor [53]) on a dislocation in the arbitrary 𝑥₁, 𝑥₂, 𝑥₃ coordinate system, decompose the Burgers vector (𝑏) to orthogonal components. This leads to the generalised definition of the J-integral in equations below. For a dislocation pile-up, the J-integral is the summation of the Peach–Koehler configurational force of the dislocations in the pile-up (including out-of-plane, 𝑏₃ [54]).

𝐽_𝑘 = ∫ 𝑃_𝑘𝑗 𝑛_𝑗 𝑑𝑆 = ∫(𝑊_𝑠 𝑛_𝑘− 𝑇_𝑖 𝑢_𝑖,𝑘) 𝑑𝑆

𝐽_𝑘^𝑥 = 𝑅_𝑘𝑗 𝐽_𝑗, 𝑖,𝑗,𝑘=1,2,3

where 𝑆 is an arbitrary contour around the dislocation pile-up with unit outward normal 𝑛_𝑖, 𝑊_𝑠 is the strain energy density, 𝑇_𝑖 = 𝜎_𝑖𝑗 𝑛_𝑗 is the traction on 𝑑𝑆, 𝑢_𝑖 are the displacement vector components, 𝐽_𝑘𝑥 is 𝐽-integral evaluated along the 𝑥_𝑘 direction, and 𝑅_𝑘𝑗 is a second-order mapping tensor that maps 𝐽_𝑘 into 𝑥_𝑘 direction. This vectorial 𝐽_𝑘-integral leads to numerical difficulties in the analysis since 𝐽₂ and, for a three-dimensional slip band or inclined crack, the 𝐽₃ terms cannot be neglected.[1]

• Deformation twinning
• Lüders band

Wikimedia Commons has media related to Slip bands in metals.

• Trochidis, A.; E., Douka; Polyzos, B. (2000-08-11). "Formation and evolution of persistent slip bands in metals". Journal of the Mechanics and Physics of Solids. 48 (8): 1761–1775. Bibcode:2000JMPSo..48.1761T. doi:10.1016/S0022-5096(99)00077-0.
• Zhang, P.; Zhang, L.; Baxevanakis, K.P.; Lu, S.; Zhao, L.G.; Bullough, C. (April 2021). "Discrete Crystal Plasticity Modelling of Slip-Controlled Cyclic Deformation and Short Crack Growth under Low Cycle Fatigue". International Journal of Fatigue. 145: 106095. doi:10.1016/j.ijfatigue.2020.106095. S2CID 230576292.