Spoke
A spoke is one of some number of rods radiating from the center of a wheel (the hub where the axle connects), connecting the hub with the round traction surface.





The term originally referred to portions of a log that had been riven (split lengthwise) into four or six sections. The radial members of a wagon wheel were made by carving a spoke (from a log) into their finished shape. A spokeshave is a tool originally developed for this purpose. Eventually, the term spoke was more commonly applied to the finished product of the wheelwright's work than to the materials they used.
History
The spoked wheel was invented to allow the construction of lighter and swifter vehicles. Earliest physical evidence for spoked wheels were found in Sintashta culture, dating to c. 2000 BCE.[1] Soon after this, horse cultures of the Caucasus region used horse-drawn spoked-wheel war chariots for the greater part of three centuries. They moved deep into the Greek peninsula where they joined with the existing Mediterranean peoples to give rise, eventually, to classical Greece after the breaking of Minoan dominance and consolidations led by pre-classical Sparta and Athens.
Neo-Chalcolithic/proto-historic period (1800-1200 BCE)[note 1] paintings in various regions of India such as Chibbar Nulla, Chhatur Bhoj Nath Nulla, Kathotia, etc. depict the usage of chariots with spoked wheels.[5][6]
Celtic chariots introduced an iron rim around the wheel in the 1st millennium BCE. The spoked wheel was in continued use without major modification until the 1870s, when wire wheels and rubber tires were invented.[7]
Construction
Spokes can be made of wood, metal, or synthetic fiber depending on whether they will be in tension or compression.
Compression spokes
The original type of spoked wheel with wooden spokes was used for horse-drawn carriages and wagons. In early motor cars, wooden spoked wheels of the artillery type were normally used.
In a simple wooden wheel, a load on the hub causes the wheel rim to flatten slightly against the ground as the lowermost wooden spoke shortens and compresses. The other wooden spokes show no significant change.
Wooden spokes are mounted radially. They are also dished, usually to the outside of the vehicle, to prevent wobbling. Also, the dishing allows the wheel to compensate for expansion of the spokes due to absorbed moisture by dishing more.[8]
Tension spokes
For use in bicycles, heavy wooden-spoked wheels were replaced by lighter wheels with spokes made of tensioned, adjustable metal wires, called wire wheels. These are also used in wheelchairs, motorcycles, automobiles, and early aircraft.
Types
Some types of wheels have removable spokes that can be replaced individually if they break or bend. These include bicycle and wheelchair wheels. High quality bicycles with conventional wheels use spokes of stainless steel, while cheaper bicycles may use galvanized (also called "rustless") or chrome plated spokes. While a good quality spoke is capable of supporting about 225 kgf (c. 500 pounds-force or 2,200 newtons) of tension, they are used at a fraction of this load to avoid suffering fatigue failures. Since bicycle and wheelchair wheel spokes are only in tension, flexible and strong materials such as synthetic fibers, are also occasionally used.[9] Metal spokes can also be ovalized or bladed to reduce aerodynamic drag, and butted (double or even triple) to reduce weight while maintaining strength.
A variation on the wire-spoked wheel was Tioga's "Tension Disk", which appeared superficially to be a solid disk but was in fact constructed using the same principles as a normal tension-spoked wheel. Instead of individual wire spokes, a continuous thread of Kevlar (aramid) was used to lace the hub to the rim under high tension. The threads were encased in a translucent disk for protection and some aerodynamic benefit, but this was not a structural component.
| wire gauge | diameter | section area |
|---|---|---|
| 15G | 1.8 mm | 3.24 mm2 |
| 14G | 2.0 mm | 4 mm2 |
| 13G | 2.3 mm | 5.29 mm2 |
| 12G | 2.6 mm | 6.76 mm2 |
| 11G | 2.9 mm | 8.41 mm2 |
| 10G | 3.2 mm | 10.24 mm2 |
Tangential lacing
Wire spokes can be radial to the hub but are more often mounted tangentially to the hub. Tangential spoking allows for the transfer of torque between the rim and the hub. Tangential spokes are thus necessary for the drive wheel, which has torque at the hub from pedalling, and any wheels using hub-mounted brakes such as disk or band brakes, which transfer torque from the rim to the brake in the opposite direction—(via the hub) when braking.
Wheelbuilding
Constructing a tension-spoked wheel from its constituent parts is called wheelbuilding and requires the correct building procedure for a strong and long-lasting end product. Tensioned spokes are usually attached to the rim or sometimes the hub with a spoke nipple. The other end is commonly peened into a disk or uncommonly bent into a "Z" to keep it from pulling through its hole in the hub. The bent version has the advantage of replacing a broken spoke in a rear bicycle wheel without having to remove the rear gears.
Wire wheels, with their excellent weight-to-strength ratio, soon became popular for light vehicles. For everyday cars, wire wheels were soon replaced by the less expensive metal disc wheel, but wire wheels remained popular for sports cars up to the 1960s. Spoked wheels are still popular on motorcycles and bicycles.
Spoke length
When building a bicycle wheel, the spokes must have the correct length, otherwise there may not be enough threads engaged, producing a weaker wheel, or they may protrude through the rim and possibly puncture the inner tube.
Calculation
For bicycle spokes, the spoke length is defined from the flange seat to the thread tip. For spokes with bent ends, the nominal spoke length does not include the width of the spoke at the bent end.
For wheels with crossed spokes (which are the norm), the desired spoke length is
where
- d = distance from the center of hub (along the axis) to flange, for example 30 mm,
- r1 = spoke hole circle radius of the hub, for example 19.5 mm,
- r2 = half of effective Rim Diameter (ERD), or the diameter the ends of the spokes make in a built wheel (see 'Discussion' attached to this article for explanation) of the rim, for example 301 mm,
- r3 = radius of spoke holes in the flange, for example 1.1 mm,
- m = number of spokes to be used for one side of the wheel, for example 36/2=18,
- k = number of crossings per spoke, for example 3 and
- a = 360° k/m, for example 360° ⋅ 3/18 = 60°.
Regarding d: For a symmetric wheel such as a front wheel with no disc brake, this is half the distance between the flanges. For an asymmetric wheel such as a front wheel with disc brake or a rear wheel with chain derailleur, the value of d is different for the left and right sides.
a is the angle between (1) the radius to a nipple hole in the rim to which a spoke is attached, and, (2) the radius to the flange hole holding the spoke. The spoke crosses either 1, 2, or 3 oppositely pointing spokes depending on the lacing design. On the flange, the angle between the radii of adjacent holes is 360°/m (for equally spaced holes). For each spoke crossed, the hub is rotated with reference to the rim one "angle between adjacent flange holes". Thus, multiplying the "angle between adjacent flange holes" by k gives the angle a. For example, a 32 spoke wheel has 16 spokes per side, 360° divided by 16 equals 22.5°. Multiply 22.5° ("angle between adjacent flange holes") by the number of crossings to get the angle a—if 3-crosses, the 32 spoke wheel has an angle a of 67.5°. Regarding r3: The size of the spoke holes in the flange does not matter for the needed spoke length. This term removes the effect of the hole size. Since the holes are usually small (just over 2 mm in diameter), the effect is small and in practice matters little.
For radially spoked wheels (zero crossings), the formula simplifies to the Pythagorean theorem, with spoke length l plus r3 being the slope, r2 minus r1 being the base, and d being the rise:
- ; or solving for the length
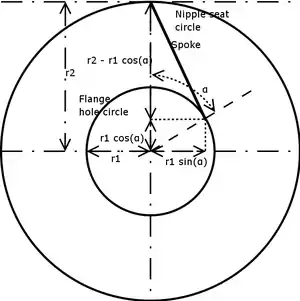
Derivation
The spoke length formula computes the length of the space diagonal of an imaginary rectangular box. Imagine holding a wheel in front of you such that a nipple is at the top. Look at the wheel from along the axis. The spoke through the top hole is now a diagonal of the imaginary box. The box has a depth of d, a height of r2-r1cos(α) and a width of r1sin(a).
Equivalently, the law of cosines may be used to first compute the length of the spoke as projected on the wheel's plane (as illustrated in the diagram), followed by an application of the Pythagorean theorem.
Notes
- Neumayer 1800-1200 BCE;[2][3] Celeste Paxton 2300-1000 BCE).[4] See Bradshaw Foundation, The Prehistoric Paintings of the Pachmarhi Hills, for proto-historic/chalocolithic.
References
- Lindner, Stephan, (2020). "Chariots in the Eurasian Steppe: a Bayesian approach to the emergence of horse-drawn transport in the earlysecond millennium BC", in Antiquity, Vol 94, Issue 374, April 2020, p. 367: "...The 12 calibrated radiocarbon dates belonging to the Sintashta horizon range between 2050 and 1760 cal BC (at 95.4% confidence; Epimakhov & Krause 2013: 137). These dates correlate well with the seven AMS-sampled Sintashta graves in the associated KA-5cemetery, which date to 2040–1730 cal BC (95.4% confidence...)".
- Neumayer, Erwin. "Chariots in the Chalcolithic Rock Art of Indian" (PDF).
- harappa.com, Chariots in the Chalcolithic Rock Art of India
- Celeste Paxton (2016), in Voices from the past: Researcher explores a mystery across 40 centuries .
- Neumayer, Erwin (28 March 2013). Prehistoric Rock Art of India. ISBN 978-0198060987.
- Neumayer, Erwin. "The Chariot in Indian Rock Art" (PDF). Harrapa.com.
- Herlihy, David (2004). Bicycle: the History. Yale University Press. p. 141. ISBN 0-300-10418-9. Retrieved 2009-09-29.
- "Hansen Wheel and Wagon Shop". 2006. Archived from the original on 2006-08-14. Retrieved 2006-08-22.
- "PBO Spoke Technology". 2006. Archived from the original on 2011-10-30. Retrieved 2011-10-21.
- "Basic spokes". Sapim N.V.
