Subgame perfect equilibrium

In game theory, a subgame perfect equilibrium (or subgame perfect Nash equilibrium) is a refinement of a Nash equilibrium used in dynamic games. A strategy profile is a subgame perfect equilibrium if it represents a Nash equilibrium of every subgame of the original game. Informally, this means that at any point in the game, the players' behavior from that point onward should represent a Nash equilibrium of the continuation game (i.e. of the subgame), no matter what happened before. Every finite extensive game with perfect recall has a subgame perfect equilibrium.[1] Perfect recall is a term introduced by Harold W. Kuhn in 1953 and "equivalent to the assertion that each player is allowed by the rules of the game to remember everything he knew at previous moves and all of his choices at those moves".[2]

Subgame Perfect Equilibrium
A solution concept in game theory
Relationship
Subset ofNash equilibrium
Intersects withEvolutionarily stable strategy
Significance
Proposed byReinhard Selten
Used forExtensive form games
ExampleUltimatum game

A common method for determining subgame perfect equilibria in the case of a finite game is backward induction. Here one first considers the last actions of the game and determines which actions the final mover should take in each possible circumstance to maximize his/her utility. One then supposes that the last actor will do these actions, and considers the second to last actions, again choosing those that maximize that actor's utility. This process continues until one reaches the first move of the game. The strategies which remain are the set of all subgame perfect equilibria for finite-horizon extensive games of perfect information.[1] However, backward induction cannot be applied to games of imperfect or incomplete information because this entails cutting through non-singleton information sets.

A subgame perfect equilibrium necessarily satisfies the one-shot deviation principle.

The set of subgame perfect equilibria for a given game is always a subset of the set of Nash equilibria for that game. In some cases the sets can be identical.

The ultimatum game provides an intuitive example of a game with fewer subgame perfect equilibria than Nash equilibria.

Example

Determining the subgame perfect equilibrium by using backward induction is shown below in Figure 1. Strategies for Player 1 are given by {Up, Uq, Dp, Dq}, whereas Player 2 has the strategies among {TL, TR, BL, BR}. There are 4 subgames in this example, with 3 proper subgames.

Figure 1

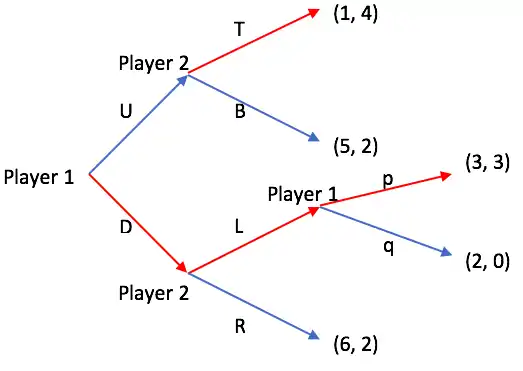
Using the backward induction, the players will take the following actions for each subgame:

  • Subgame for actions p and q: Player 1 will take action p with payoff (3, 3) to maximize Player 1's payoff, so the payoff for action L becomes (3,3).
  • Subgame for actions L and R: Player 2 will take action L for 3 > 2, so the payoff for action D becomes (3, 3).
  • Subgame for actions T and B: Player 2 will take action T to maximize Player 2's payoff, so the payoff for action U becomes (1, 4).
  • Subgame for actions U and D: Player 1 will take action D to maximize Player 1's payoff.

Thus, the subgame perfect equilibrium is {Dp, TL} with the payoff (3, 3).

An extensive-form game with incomplete information is presented below in Figure 2. Note that the node for Player 1 with actions A and B, and all succeeding actions is a subgame. Player 2's nodes are not a subgame as they are part of the same information set.

Figure 2

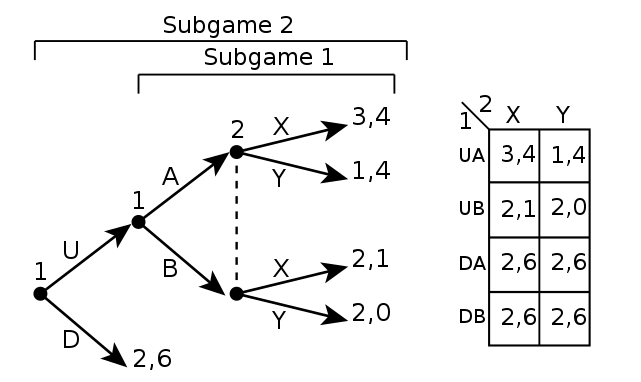
The first normal-form game is the normal form representation of the whole extensive-form game. Based on the provided information, (UA, X), (DA, Y), and (DB, Y) are all Nash equilibria for the entire game.

The second normal-form game is the normal form representation of the subgame starting from Player 1's second node with actions A and B. For the second normal-form game, the Nash equilibrium of the subgame is (A, X).

For the entire game Nash equilibria (DA, Y) and (DB, Y) are not subgame perfect equilibria because the move of Player 2 does not constitute a Nash equilibrium. The Nash equilibrium (UA, X) is subgame perfect because it incorporates the subgame Nash equilibrium (A, X) as part of its strategy.[3]

To solve this game, first find the Nash Equilibria by mutual best response of Subgame 1. Then use backwards induction and plug in (A,X) → (3,4) so that (3,4) become the payoffs for Subgame 2.[3]

The dashed line indicates that player 2 does not know whether player 1 will play A or B in a simultaneous game.

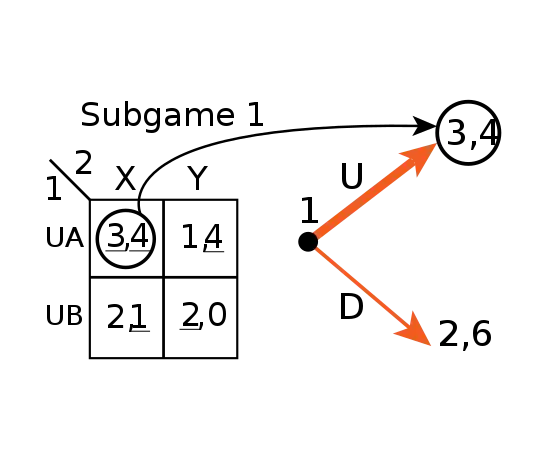
Subgame 1 is solved and (3,4) replaces all of Subgame 1 and player one will choose U -> (3,4)Solution for Subgame 1

Player 1 chooses U rather than D because 3 > 2 for Player 1's payoff. The resulting equilibrium is (A, X) → (3,4).

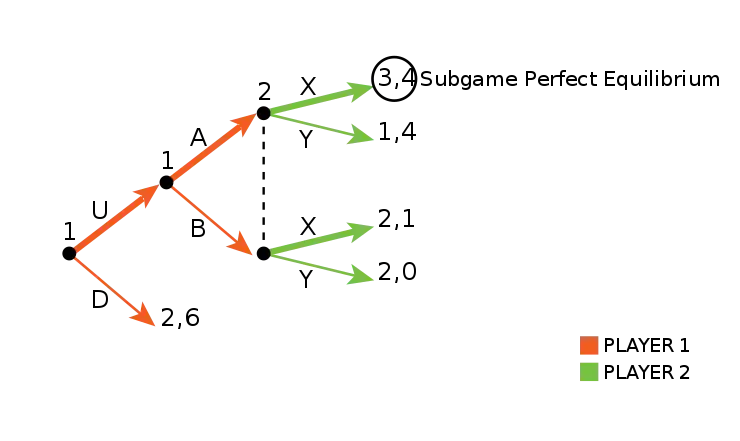
Solution of Subgame Perfect Equilibrium

Thus, the subgame perfect equilibrium through backwards induction is (UA, X) with the payoff (3, 4).

Repeated games

For finitely repeated games, if a stage game has only one unique Nash equilibrium, the subgame perfect equilibrium is to play without considering past actions, treating the current subgame as a one-shot game. An example of this is a finitely repeated Prisoner's dilemma game. The Prisoner's dilemma gets its name from a situation that contains two guilty culprits. When they are interrogated, they have the option to stay quiet or defect. If both culprits stay quiet, they both serve a short sentence. If both defect, they both serve a moderate sentence. If they choose opposite options, then the culprit that defects is free and the culprit who stays quiet serves a long sentence. Ultimately, using backward induction, the last subgame in a finitely repeated Prisoner's dilemma requires players to play the unique Nash equilibrium (both players defecting). Because of this, all games prior to the last subgame will also play the Nash equilibrium to maximize their single-period payoffs.[4] If a stage-game in a finitely repeated game has multiple Nash equilibria, subgame perfect equilibria can be constructed to play non-stage-game Nash equilibrium actions, through a "carrot and stick" structure. One player can use the one stage-game Nash equilibrium to incentivize playing the non-Nash equilibrium action, while using a stage-game Nash equilibrium with lower payoff to the other player if they choose to defect.[5]

Finding subgame-perfect equilibria
One game in which the backward induction solution is well known is tic-tac-toe

Reinhard Selten proved that any game which can be broken into "sub-games" containing a sub-set of all the available choices in the main game will have a subgame perfect Nash Equilibrium strategy (possibly as a mixed strategy giving non-deterministic sub-game decisions). Subgame perfection is only used with games of complete information. Subgame perfection can be used with extensive form games of complete but imperfect information.

The subgame-perfect Nash equilibrium is normally deduced by "backward induction" from the various ultimate outcomes of the game, eliminating branches which would involve any player making a move that is not credible (because it is not optimal) from that node. One game in which the backward induction solution is well known is tic-tac-toe, but in theory even Go has such an optimum strategy for all players. The problem of the relationship between subgame perfection and backward induction was settled by Kaminski (2019), who proved that a generalized procedure of backward induction produces all subgame perfect equilibria in games that may have infinite length, infinite actions as each information set, and imperfect information if a condition of final support is satisfied.

The interesting aspect of the word "credible" in the preceding paragraph is that taken as a whole (disregarding the irreversibility of reaching sub-games) strategies exist which are superior to subgame perfect strategies, but which are not credible in the sense that a threat to carry them out will harm the player making the threat and prevent that combination of strategies. For instance in the game of "chicken" if one player has the option of ripping the steering wheel from their car they should always take it because it leads to a "sub game" in which their rational opponent is precluded from doing the same thing (and killing them both). The wheel-ripper will always win the game (making his opponent swerve away), and the opponent's threat to suicidally follow suit is not credible.

See also

References
  1. Osborne, M. J. (2004). An Introduction to Game Theory. Oxford University Press.
  2. Kuhn, Harold William; Tucker, Albert William (2 March 2016). Contributions to the Theory of Games (AM-28), Volume II. Princeton University Press. ISBN 978-1-4008-8197-0.
  3. Joel., Watson (2013-05-09). Strategy : an introduction to game theory (Third ed.). New York. ISBN 9780393918380. OCLC 842323069.{{cite book}}: CS1 maint: location missing publisher (link)
  4. Yildiz, Muhamet (2012). "12 Repeated Games". 14.12 Economic Applications of Game Theory. Massachusetts Institute of Technology: MIT OpenCourseWare. Retrieved April 27, 2021.
  5. Takako, Fujiwara-Greve (27 June 2015). Non-cooperative game theory. Tokyo. ISBN 9784431556442. OCLC 911616270.{{cite book}}: CS1 maint: location missing publisher (link)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.