Subpaving
In mathematics, a subpaving is a set of nonoverlapping boxes of R⁺. A subset X of Rⁿ can be approximated by two subpavings X⁻ and X⁺ such that
X⁻ ⊂ X ⊂ X⁺.
In R¹ the boxes are line segments, in R² rectangles and in Rⁿ hyperrectangles. A R² subpaving can be also a "non-regular tiling by rectangles", when it has no holes.
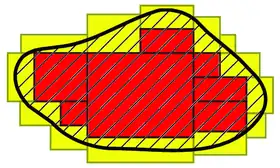
Boxes present the advantage of being very easily manipulated by computers, as they form the heart of interval analysis. Many interval algorithms naturally provide solutions that are regular subpavings.[1]
In computation, a well-known application of subpaving in R² is the Quadtree data structure. In image tracing context and other applications is important to see X⁻ as topological interior, as illustrated.
Example
The three figures on the right below show an approximation of the set
X = {(x1, x2) ∈ R2 | x2
1 + x2
2 +
sin(x1 + x2) ∈ [4,9]}
with different accuracies. The set X⁻ corresponds to red boxes and the set X⁺ contains all red and yellow boxes.
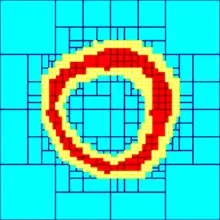
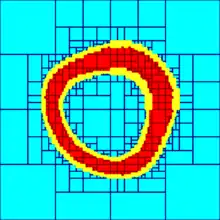
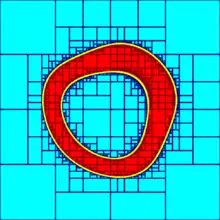
Combined with interval-based methods, subpavings are used to approximate the solution set of non-linear problems such as set inversion problems.[2] Subpavings can also be used to prove that a set defined by nonlinear inequalities is path connected,[3] to provide topological properties of such sets,[4] to solve piano-mover's problems[5] or to implement set computation.[6]
References
- Kieffer, M.; Braems, I.; Walter, É.; Jaulin, L. (2001). "Guaranteed Set Computation with Subpavings" (PDF). Scientific Computing, Validated Numerics, Interval Methods. pp. 167–172. doi:10.1007/978-1-4757-6484-0_14. ISBN 978-1-4419-3376-8.
- Jaulin, Luc; Walter, Eric (1993). "Set inversion via interval analysis for nonlinear bounded-error estimation" (PDF). Automatica. 29 (4): 1053–1064. doi:10.1016/0005-1098(93)90106-4.
- Delanoue, N.; Jaulin, L.; Cottenceau, B. (2005). "Using interval arithmetic to prove that a set is path-connected" (PDF). Theoretical Computer Science. 351 (1).
-
Delanoue, N.; Jaulin, L.; Cottenceau, B. (2006). "Counting the Number of Connected Components of a Set and Its Application to Robotics" (PDF). Applied Parallel Computing. State of the Art in Scientific Computing. pp. 93–101. doi:10.1007/11558958_11. ISBN 978-3-540-29067-4.
{{cite book}}:|journal=ignored (help) - Jaulin, L. (2001). "Path planning using intervals and graphs" (PDF). Reliable Computing. 7 (1).
- Kieffer, M.; Jaulin, L.; Braems, I.; Walter, E. (2001). "Guaranteed Set Computation with Subpavings" (PDF). Scientific Computing, Validated Numerics, Interval Methods. In W. Kraemer and J. W. Gudenberg (Eds), Scientific Computing, Validated Numerics, Interval Methods, Kluwer Academic Publishers. pp. 167–178. doi:10.1007/978-1-4757-6484-0_14. ISBN 978-1-4419-3376-8.