Proof without words

A proof without words for the sum of odd numbers theorem.

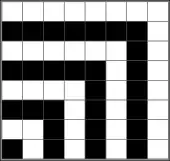
The statement that the sum of all positive odd numbers up to 2n − 1 is a perfect square—more specifically, the perfect square n²—can be demonstrated by a proof without words.[3]

In one corner of a grid, a single block represents 1, the first square. That can be wrapped on two sides by a strip of three blocks (the next odd number) to make a 2 × 2 block: 4, the second square. Adding a further five blocks makes a 3 × 3 block: 9, the third square. This process can be continued indefinitely.

Rearrangement proof of the Pythagorean theorem. The uncovered area of gray space remains constant before and after the rearrangement of the triangles: on the left it is shown to equal c², and on the right a²+b².

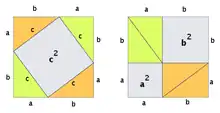
The Pythagorean theorem that ${\displaystyle a^{2}+b^{2}=c^{2}}$ can be proven without words.[4]

One method of doing so is to visualise a larger square of sides ${\displaystyle a+b}$, with four right-angled triangles of sides ${\displaystyle a}$, ${\displaystyle b}$ and ${\displaystyle c}$ in its corners, such that the space in the middle is a diagonal square with an area of ${\displaystyle c^{2}}$. The four triangles can be rearranged within the larger square to split its unused space into two squares of ${\displaystyle a^{2}}$ and ${\displaystyle b^{2}}$.[5]

A graphical proof of Jensen's inequality.

Jensen's inequality can also be proven graphically. A dashed curve along the X axis is the hypothetical distribution of X, while a dashed curve along the Y axis is the corresponding distribution of Y values. The convex mapping Y(X) increasingly "stretches" the distribution for increasing values of X.[6]