Forensic epidemiology

The metric of a case-specific FE analysis of cause is the comparative risk ratio (CRR). The CRR is a unique metric to FE; it allows for the comparison of probabilities applicable to the investigated circumstances of an individual injury or disease. Because a CRR is based on the unique circumstances surrounding the injury or disease of an individual, it may or may not be derived from a population-based relative risk (RR) or odds ratio (OR). An example of an RR analysis that could be used as a CRR is as follows: for an unbelted driver who was seriously injured in a traffic crash, an important causal question might be what role the failure to use a seat belt played in causing his injury. A relevant RR analysis would consist of the examination of the frequency of serious injury in 1000 randomly selected unbelted drivers exposed to a 20 mph frontal collision versus the frequency of serious injury in 1000 randomly selected restrained drivers exposed to the same collision severity and type. If the frequency of serious injury in the group exposed to the presumptive hazard (failure to use a seat belt) was 0.15 and the frequency in the unexposed (belted) group was 0.05, then the CRR would be the same thing as the RR of 0.15/0.05. The RR design of the analysis dictates that the populations that the numerator and denominator of the CRR are substantially similar in all respects, with the exception of the exposure to the investigated hazard, which was the failure to use a seat belt in the example.

In some instances encountered in a legal setting, however, the numerator and denominator risk must be derived from dissimilar populations in order to fit the circumstances of an investigated injury or disease. In such a case the CRR cannot be derived from either an RR or OR. An example of such a situation occurs when the numerator is a per event risk, and the denominator is a per-time risk (also known as a cumulative risk). An example of this type of analysis would be the investigation of a pulmonary embolism (PE) that occurred a week after a patient sustained a lower extremity fracture in a traffic crash. Such complications often result from blood clots forming in the legs and then traveling to the lungs. If the patient had a history of deep vein thrombosis (DVT) in the lower extremities prior to the crash, then a CRR might consist of the comparison between the risk of a PE following a lower extremity fracture (a per event rate) and the 1-week risk of PE in a patient with DVT (a time-dependent probability).

Another example of a CRR based on dissimilar populations is when there are only a limited number of potential causes to be compared. An example is the investigation of the cause of an adverse reaction in a person who took two different drugs at the same time, both of which could have caused the reaction (and which, for the example, do not interact with each other). In such a situation, the CRR applicable to the unique circumstances experienced by the individual could be estimated by comparing the adverse reaction rate for the two drugs.

The attributable proportion under the exposed (AP_e ) is an indication of the proportion of patients who were exposed to the potential cause and got sick because of this exposure. It can only be used if the RR >1 and can be calculated by [(RR-1)/RR X 100%]. When the CRR is based on an RR, these formulae also apply to the CRR. The result of the analysis, given as an RR, CRR, or AP_e , meets the legal standard of what is “more likely true than not,” when the RR or CRR is >2.0 (with a 95% confidence interval lower boundary of >1.0), or the AP_e is >50%. The AP_e is also known as the "Probability of Causation (PC)" a term that is defined in the US Code of Federal Regulations (Federal Register / Vol. 67, No. 85 / Thursday, May 2, 2002 / Rules and Regulations p. 22297) and elsewhere.

Analysis of causation, particularly for injury or other conditions with a relatively short latency period between exposure and outcome, is accomplished using a 3-step approach, as follows:[5]

1. Plausibility: This first step addresses whether it is biologically possible for the injury event to have caused the condition (a.k.a. general causation), and follows a special application of the viewpoints set forth by Hill (see below). A finding of plausibility is unrelated to the frequency of the injury, because even if the injury occurs in only 1 in 100 or fewer cases of exposure to the event, it is still plausibly caused by the event. Plausibility is a relatively low hurdle to clear in a causal analysis, and is largely satisfied by the lack of evidence of implausibility of the relationship. Plausibility is often, but not necessarily, established with epidemiologic data or information.
2. Temporality: This second step examines the clinical and other evidence of the timing between the onset of the symptoms of injury and the injury event, and must be satisfied to assess specific causation. First, it must be established that the sequence of the injury and the event is appropriate; the symptoms cannot be identically present prior to the event. Further, the onset of the symptoms of injury cannot be either too latent or insufficiently latent, depending on the nature of the exposure and outcome.
3. Lack of a more probable alternative explanation: This final step examines the probability of the injury condition occurring at the same point in time in the individual, given what is known about the individual from the review of medical records and other evidence, but in the absence of the injury event (a.k.a. differential diagnosis). First, evidence of competing injury events must be evaluated, and compared for risk (often via analysis of epidemiologic data). Then, the likelihood of the condition occurring spontaneously must be assessed, given the known history of the individual.

The 3-step methodology was challenged in United States District Court for the District of Colorado in Etherton v Auto-Owners Insurance Company. The defendant challenged, among other things, the reliability and fit of the methods described by the expert. After an extensive examination and discussion of the 3-step process used by the expert, the court found that the methodology appropriately fit the specific facts of the case, and that a population-based (epidemiologic) approach was an appropriate part of the causal methodology. The court denied the defendant’s motion to strike the expert’s testimony in the order, which was entered on 3/31/14.

The Defendant appealed the ruling from the District Court, and in July 2016, the Tenth Circuit U.S. Court of Appeals affirmed the 3-step causal methodology as generally accepted and well established for assessing injury causation, under the Daubert standard. See Etherton v. Auto-Owners Insurance Company, No. 14-1164 (10th Cir, 7/19/16).

Plausibility of an investigated association can be assessed in an FE investigation, in part, via application of the Hill criteria, named for a 1965 publication by Sir Austin Bradford-Hill, in which he described nine “viewpoints” by which an association described in an epidemiologic study could be assessed for causality.[6] Hill declined to call his viewpoints “criteria” lest they be considered a checklist for assessing causation. The term “ Hill criteria” is used widely in the literature, however, and for convenience is used in the present discussion. Of the nine criteria, there are seven that have utility for assessing the plausibility of an investigated specific causal relationship, as follows:

• Coherence: A causal conclusion should not contradict present substantive knowledge. It should “ make sense” given current knowledge
• Analogy: The results of a previously described causal relationship may be translatable to the circumstances of a current investigation
• Consistency: The repeated observation of the investigated relationship in different circumstances or across a number of studies lends strength to a causal inference
• Specificity: The degree to which the exposure is associated with a particular outcome
• Biological plausibility: The extent to which the observed association can be explained by known scientific principles
• Experiment: In some cases there may be evidence from randomized experiments (i.e., drug trials)
• Dose response: The probability, frequency, or severity of the outcome increases with increased amount of exposure

The triangular relationship between exposure, outcome, and confounder. When investigating whether there is a causal relationship between an exposure and outcome of interest, the influence of extraneous variables needs to be taken into account. A confounder is defined as a concurrent cause of the outcome under investigation that is related to, but not a consequence of, the exposure of interest.

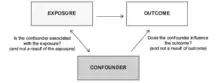
Subsequent authors have added the feature of Challenge/ Dechallenge/ Rechallenge for circumstances when the exposure is repeated over time and there is the ability to observe the associated outcome response, as might occur with an adverse reaction to a medication. Additional considerations when assessing an association are the potential impact of confounding and bias in the data, which can obscure a true relationship. Confounding refers to a situation in which an association between an exposure and outcome is all or partly the result of a factor that affects the outcome but is unaffected by the exposure. Bias refers to a form of error that may threaten the validity of a study by producing results that are systematically different from the true results. Two main categories of bias in epidemiologic studies are selection bias, which occurs when study subjects are selected as a result of another unmeasured variable that is associated with both the exposure and outcome of interest; and information bias, which is systematic error in the assessment of a variable. While useful when assessing a previously unexplored association, there is no combination or minimal number of these criteria that must be met in order to conclude that a plausible relationship exists between a known exposure and an observed outcome.

In many FE investigations there is no need for a causal plausibility analysis if a general causal relationship is well established. In large part, plausibility of a relationship is entertained once implausibility has been rejected. The two remaining Hill criteria are temporality and strength of association. While both criteria have utility in assessing specific causation, temporality is the feature of an association that must be present, at least with regard to sequence (i.e., the exposure must precede the outcome), in order to consider a relationship causal. Temporal proximity can also be useful in some specific causation evaluations, as the closer the investigated exposure and the outcome are in time the less opportunity there is for an intervening cause to act. Another feature of temporality that may have a role in a specific causation evaluation is latency. An outcome may occur too soon or too long after an exposure to be considered causally related. As an example, some food borne illnesses must incubate for hours or days after ingestion, and thus an illness that begins directly following a meal, and which is later found to be caused by a food borne microorganism that requires >12 h incubation, was not caused by the investigated meal, even if an investigation were to reveal the microorganism in the ingested food. Strength of association is the criterion that is used in general causation to assess the impact of the exposure on the population, and is often quantified in terms of RR. In a specific causation evaluation the strength of the association between the exposure and the outcome is quantified by the CRR, as described above.

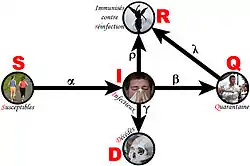
A contingency table, also called a crosstabulation, of possible test outcomes, and the associated equations for evaluating test accuracy.

Test accuracy investigation is a standard practice in clinical epidemiology. In this setting, a diagnostic test is scrutinized to determine by various measures how often a test result is correct. In FE the same principles are used to evaluate the accuracy of proposed tests leading to conclusions that are central to fact finder determinations of guilt or innocence in criminal investigations, and of causality in civil matters. The utility of a test is highly dependent on its accuracy, which is determined by a measure of how often a positive or negative test result truly represents the actual status that is being tested. For any test or criterion there are typically four possible results: (1) a true positive (TP), in which the test correctly identifies tested subjects with the condition of interest; (2) a true negative (TN), in which the test correctly identifies test subjects who do not have the condition of interest; (3) a false positive (FP), in which the test is positive even though condition is not present, and; (4) a false negative (FN) in which the test is negative even though the condition is present. Fig. 3.19 is a contingency table illustrating the relationships between test results and condition presence, as well as the following test accuracy parameters:

• Sensitivity (the rate at which the test is positive when the condition is present) TP/(TP + FN)
• Specificity (the rate at which the test is negative when the condition is absent) TN/(TN + FP)
• Positive predictive value (the rate at which the condition is present when the test is positive) TP/(TP + FP)
• Negative predictive value (the rate at which the condition is absent when the test is negative) TN/(TN + FN)

Probability is used to characterize the degree of belief in the truth of an assertion. The basis for such a belief can be a physical system that produces outcomes at a rate that is uniform over time, such as a gaming device like a roulette wheel or a die. With such a system, the observer does not influence the outcome; a fair six-sided die that is rolled enough times will land on any one of its sides 1/6th of the time. An assertion of a probability based in a physical system is easily tested with sufficient randomized experimentation. Conversely, the basis for a high degree of belief in an asserted claim may be a personally held perspective that cannot be tested. This does not mean that the assertion is any less true than one that can be tested. As an example, one might truthfully assert that “if I eat a banana there is a high probability that it will make me nauseous” based upon experience unknown to anyone but one’s self. It is difficult to test such assertions, which are evaluated through collateral evidence of plausibility and analogy, often based on similar personal experience. In forensic settings, assertions of belief are often characterized as probabilities, that is, what is most likely, for a given set of facts. For circumstances in which a variety of conditions exist that may modify or “ condition” the probability of a particular outcome or scenario, a method of quantifying the relationship between the modifying conditions and the probability of the outcome employs Bayesian reasoning, named for Bayes’ Theorem or Law upon which the approach is based. Most simply stated, Bayes’ Law allows for a more precise quantification of the uncertainty in a given probability. As applied in a forensic setting, Bayes’ Law tells us what we want to know given what we do know. Although Bayes’ Law is known in forensic sciences primarily for its application to DNA evidence, a number of authors have described the use of Bayesian reasoning for other applications in forensic medicine, including identification and age estimation.

The post-test probability is a highly useful Bayesian equation that allows for the calculation of the probability that a condition is present when the test is positive, conditioned by the pretest prevalence of the condition of interest. This equation is given in box to the right:

Post-test probability equation

The equation results in a positive predictive value for a given pre-event or pretest prevalence. In a circumstance in which the pretest prevalence is considered “indifferent” the prevalence and (1-prevalence) values cancel out, and the calculation is a simplified to a positive predictive value.