Lagrange point
In celestial mechanics, the Lagrange points (/ləˈɡrɑːndʒ/; also Lagrangian points or libration points) are points of equilibrium for small-mass objects under the influence of two massive orbiting bodies. Mathematically, this involves the solution of the restricted three-body problem in which two bodies are far more massive than the third.[1]

| Part of a series on |
| Astrodynamics |
|---|
 |
|
Celestial mechanics |
|
Engineering and efficiency |
Normally, the two massive bodies exert an unbalanced gravitational force at a point, altering the orbit of whatever is at that point. At the Lagrange points, the gravitational forces of the two large bodies and the centrifugal force balance each other.[2] This can make Lagrange points an excellent location for satellites, as few orbit corrections are needed to maintain the desired orbit. Small objects placed in orbit at Lagrange points are in equilibrium in at least two directions relative to the center of mass of the large bodies.
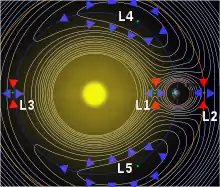
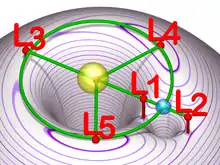
For any combination of two orbital bodies there are five Lagrange points, L1 to L5, all in the orbital plane of the two large bodies. There are five Lagrange points for the Sun–Earth system, and five different Lagrange points for the Earth–Moon system. L1, L2, and L3 are on the line through the centers of the two large bodies, while L4 and L5 each act as the third vertex of an equilateral triangle formed with the centers of the two large bodies.
When the mass ratio of the two bodies is large enough, the L4 and L5 points are stable points meaning that objects can orbit them, and that they have a tendency to pull objects into them. Several planets have trojan asteroids near their L4 and L5 points with respect to the Sun; Jupiter has more than one million of these trojans. Artificial satellites, for example the James Webb Space Telescope, have been placed at L1 and L2 with respect to the Sun and Earth, and with respect to the Earth and the Moon.[3] The Lagrange points have been proposed for uses in space exploration.
History
The three collinear Lagrange points (L1, L2, L3) were discovered by Leonhard Euler around 1750, a decade before Joseph-Louis Lagrange discovered the remaining two.[4][5]
In 1772, Lagrange published an "Essay on the three-body problem". In the first chapter he considered the general three-body problem. From that, in the second chapter, he demonstrated two special constant-pattern solutions, the collinear and the equilateral, for any three masses, with circular orbits.[6]
Lagrange points
The five Lagrange points are labelled and defined as follows:
L1 point
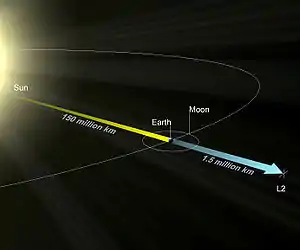
The L1 point lies on the line defined between the two large masses M1 and M2. It is the point where the gravitational attraction of M2 and that of M1 combine to produce an equilibrium. An object that orbits the Sun more closely than Earth would normally have a shorter orbital period than Earth, but that ignores the effect of Earth's own gravitational pull. If the object is directly between Earth and the Sun, then Earth's gravity counteracts some of the Sun's pull on the object, and therefore increases the orbital period of the object. The closer to Earth the object is, the greater this effect is. At the L1 point, the orbital period of the object becomes exactly equal to Earth's orbital period. L1 is about 1.5 million kilometers from Earth, or 0.01 au.[1]
L2 point
The L2 point lies on the line through the two large masses, beyond the smaller of the two. Here, the gravitational forces of the two large masses balance the centrifugal effect on a body at L2. On the opposite side of Earth from the Sun, the orbital period of an object would normally be greater than that of Earth. The extra pull of Earth's gravity decreases the orbital period of the object, and at the L2 point that orbital period becomes equal to Earth's. Like L1, L2 is about 1.5 million kilometers or 0.01 au from Earth. An example of a spacecraft at L2 is the James Webb Space Telescope, designed to operate near the Earth–Sun L2.[7] Earlier examples include the Wilkinson Microwave Anisotropy Probe and its successor, Planck.
L3 point
The L3 point lies on the line defined by the two large masses, beyond the larger of the two. Within the Sun–Earth system, the L3 point exists on the opposite side of the Sun, a little outside Earth's orbit and slightly closer to the center of the Sun than Earth is. This placement occurs because the Sun is also affected by Earth's gravity and so orbits around the two bodies' barycenter, which is well inside the body of the Sun. An object at Earth's distance from the Sun would have an orbital period of one year if only the Sun's gravity is considered. But an object on the opposite side of the Sun from Earth and directly in line with both "feels" Earth's gravity adding slightly to the Sun's and therefore must orbit a little farther from the barycenter of Earth and Sun in order to have the same 1-year period. It is at the L3 point that the combined pull of Earth and Sun causes the object to orbit with the same period as Earth, in effect orbiting an Earth+Sun mass with the Earth-Sun barycenter at one focus of its orbit.
L4 and L5 points
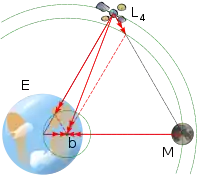
The L4 and L5 points lie at the third vertices of the two equilateral triangles in the plane of orbit whose common base is the line between the centers of the two masses, such that the point lies 60° ahead of (L4) or behind (L5) the smaller mass with regard to its orbit around the larger mass.
Stability
The triangular points (L4 and L5) are stable equilibria, provided that the ratio of M1/M2 is greater than 24.96.[note 1] This is the case for the Sun–Earth system, the Sun–Jupiter system, and, by a smaller margin, the Earth–Moon system. When a body at these points is perturbed, it moves away from the point, but the factor opposite of that which is increased or decreased by the perturbation (either gravity or angular momentum-induced speed) will also increase or decrease, bending the object's path into a stable, kidney bean-shaped orbit around the point (as seen in the corotating frame of reference).[8]
The points L1, L2, and L3 are positions of unstable equilibrium. Any object orbiting at L1, L2, or L3 will tend to fall out of orbit; it is therefore rare to find natural objects there, and spacecraft inhabiting these areas must employ station keeping in order to maintain their position.
Natural objects at Lagrange points
Due to the natural stability of L4 and L5, it is common for natural objects to be found orbiting in those Lagrange points of planetary systems. Objects that inhabit those points are generically referred to as 'trojans' or 'trojan asteroids'. The name derives from the names that were given to asteroids discovered orbiting at the Sun–Jupiter L4 and L5 points, which were taken from mythological characters appearing in Homer's Iliad, an epic poem set during the Trojan War. Asteroids at the L4 point, ahead of Jupiter, are named after Greek characters in the Iliad and referred to as the "Greek camp". Those at the L5 point are named after Trojan characters and referred to as the "Trojan camp". Both camps are considered to be types of trojan bodies.
As the Sun and Jupiter are the two most massive objects in the Solar System, there are more Sun–Jupiter trojans than for any other pair of bodies. However, smaller numbers of objects are known at the Lagrange points of other orbital systems:
- The Sun–Earth L4 and L5 points contain interplanetary dust and at least two asteroids, 2010 TK7 and 2020 XL5.[9][10][11]
- The Earth–Moon L4 and L5 points contain concentrations of interplanetary dust, known as Kordylewski clouds.[12][13] Stability at these specific points is greatly complicated by solar gravitational influence.[14]
- The Sun–Neptune L4 and L5 points contain several dozen known objects, the Neptune trojans.[15]
- Mars has four accepted Mars trojans: 5261 Eureka, 1999 UJ7, 1998 VF31, and 2007 NS2.
- Saturn's moon Tethys has two smaller moons of Saturn in its L4 and L5 points, Telesto and Calypso. Another Saturn moon, Dione also has two Lagrange co-orbitals, Helene at its L4 point and Polydeuces at L5. The moons wander azimuthally about the Lagrange points, with Polydeuces describing the largest deviations, moving up to 32° away from the Saturn–Dione L5 point.
- One version of the giant impact hypothesis postulates that an object named Theia formed at the Sun–Earth L4 or L5 point and crashed into Earth after its orbit destabilized, forming the Moon.[16]
- In binary stars, the Roche lobe has its apex located at L1; if one of the stars expands past its Roche lobe, then it will lose matter to its companion star, known as Roche lobe overflow.
Objects which are on horseshoe orbits are sometimes erroneously described as trojans, but do not occupy Lagrange points. Known objects on horseshoe orbits include 3753 Cruithne with Earth, and Saturn's moons Epimetheus and Janus.
Physical and mathematical details
Click for animation.
Lagrange points are the constant-pattern solutions of the restricted three-body problem. For example, given two massive bodies in orbits around their common barycenter, there are five positions in space where a third body, of comparatively negligible mass, could be placed so as to maintain its position relative to the two massive bodies. As seen in a rotating reference frame that matches the angular velocity of the two co-orbiting bodies, the gravitational fields of two massive bodies combined providing the centripetal force at the Lagrange points, allowing the smaller third body to be relatively stationary with respect to the first two.
L1
The location of L1 is the solution to the following equation, gravitation providing the centripetal force:
where r is the distance of the L1 point from the smaller object, R is the distance between the two main objects, and M1 and M2 are the masses of the large and small object, respectively. The quantity in parentheses on the right is the distance of L1 from the center of mass. Solving this for r involves solving a quintic function, but if the mass of the smaller object (M2) is much smaller than the mass of the larger object (M1) then L1 and L2 are at approximately equal distances r from the smaller object, equal to the radius of the Hill sphere, given by:
We may also write this as:
Since the tidal effect of a body is proportional to its mass divided by the distance cubed, this means that the tidal effect of the smaller body at the L1 or at the L2 point is about three times of that body. We may also write:
where ρ1 and ρ2 are the average densities of the two bodies and and are their diameters. The ratio of diameter to distance gives the angle subtended by the body, showing that viewed from these two Lagrange points, the apparent sizes of the two bodies will be similar, especially if the density of the smaller one is about thrice that of the larger, as in the case of the earth and the sun.
This distance can be described as being such that the orbital period, corresponding to a circular orbit with this distance as radius around M2 in the absence of M1, is that of M2 around M1, divided by √3 ≈ 1.73:
L2
The location of L2 is the solution to the following equation, gravitation providing the centripetal force:
with parameters defined as for the L1 case. Again, if the mass of the smaller object (M2) is much smaller than the mass of the larger object (M1) then L2 is at approximately the radius of the Hill sphere, given by:
The same remarks about tidal influence and apparent size apply as for the L1 point. For example, the angular radius of the sun as viewed from L2 is arcsin(695.5×103/151.1×106) ≈ 0.264°, whereas that of the earth is arcsin(6371/1.5×106) ≈ 0.242°. Looking toward the sun from L2 one sees an annular eclipse. It is necessary for a spacecraft, like Gaia, to follow a Lissajous orbit or a halo orbit around L2 in order for its solar panels to get full sun.
L3
The location of L3 is the solution to the following equation, gravitation providing the centripetal force:
with parameters M1, M2, and R defined as for the L1 and L2 cases, and r now indicates the distance of L3 from the position of the smaller object, if it were rotated 180 degrees about the larger object, while positive r implying L3 is closer to the larger object than the smaller object. If the mass of the smaller object (M2) is much smaller than the mass of the larger object (M1), then:[18]
L4 and L5
The reason these points are in balance is that at L4 and L5 the distances to the two masses are equal. Accordingly, the gravitational forces from the two massive bodies are in the same ratio as the masses of the two bodies, and so the resultant force acts through the barycenter of the system; additionally, the geometry of the triangle ensures that the resultant acceleration is to the distance from the barycenter in the same ratio as for the two massive bodies. The barycenter being both the center of mass and center of rotation of the three-body system, this resultant force is exactly that required to keep the smaller body at the Lagrange point in orbital equilibrium with the other two larger bodies of the system (indeed, the third body needs to have negligible mass). The general triangular configuration was discovered by Lagrange working on the three-body problem.
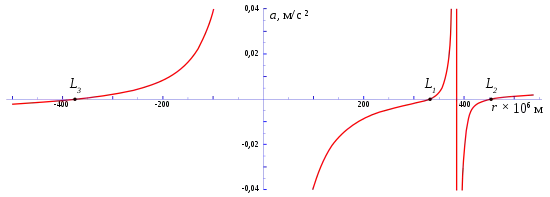
Radial acceleration
The radial acceleration a of an object in orbit at a point along the line passing through both bodies is given by:
where r is the distance from the large body M1, R is the distance between the two main objects, and sgn(x) is the sign function of x. The terms in this function represent respectively: force from M1; force from M2; and centripetal force. The points L3, L1, L2 occur where the acceleration is zero — see chart at right. Positive acceleration is acceleration towards the right of the chart and negative acceleration is towards the left; that is why acceleration has opposite signs on opposite sides of the gravity wells.
Stability

Although the L1, L2, and L3 points are nominally unstable, there are quasi-stable periodic orbits called halo orbits around these points in a three-body system. A full n-body dynamical system such as the Solar System does not contain these periodic orbits, but does contain quasi-periodic (i.e. bounded but not precisely repeating) orbits following Lissajous-curve trajectories. These quasi-periodic Lissajous orbits are what most of Lagrangian-point space missions have used until now. Although they are not perfectly stable, a modest effort of station keeping keeps a spacecraft in a desired Lissajous orbit for a long time.
For Sun–Earth-L1 missions, it is preferable for the spacecraft to be in a large-amplitude (100,000–200,000 km or 62,000–124,000 mi) Lissajous orbit around L1 than to stay at L1, because the line between Sun and Earth has increased solar interference on Earth–spacecraft communications. Similarly, a large-amplitude Lissajous orbit around L2 keeps a probe out of Earth's shadow and therefore ensures continuous illumination of its solar panels.
The L4 and L5 points are stable provided that the mass of the primary body (e.g. the Earth) is at least 25[note 1] times the mass of the secondary body (e.g. the Moon),[19][20] and the mass of the secondary is at least 10 times that of the tertiary (e.g. the satellite). The Earth is over 81 times the mass of the Moon (the Moon is 1.23% of the mass of the Earth[21]). Although the L4 and L5 points are found at the top of a "hill", as in the effective potential contour plot above, they are nonetheless stable. The reason for the stability is a second-order effect: as a body moves away from the exact Lagrange position, Coriolis acceleration (which depends on the velocity of an orbiting object and cannot be modeled as a contour map)[20] curves the trajectory into a path around (rather than away from) the point.[20][22] Because the source of stability is the Coriolis force, the resulting orbits can be stable, but generally are not planar, but "three-dimensional": they lie on a warped surface intersecting the ecliptic plane. The kidney-shaped orbits typically shown nested around L4 and L5 are the projections of the orbits on a plane (e.g. the ecliptic) and not the full 3-D orbits.
Solar System values
This table lists sample values of L1, L2, and L3 within the Solar System. Calculations assume the two bodies orbit in a perfect circle with separation equal to the semimajor axis and no other bodies are nearby. Distances are measured from the larger body's center of mass with L3 showing a negative location. The percentage columns show how the distances compare with the semimajor axis. E.g. for the Moon, L1 is located 326400 km from Earth's center, which is 84.9% of the Earth–Moon distance or 15.1% in front of the Moon; L2 is located 448900 km from Earth's center, which is 116.8% of the Earth–Moon distance or 16.8% beyond the Moon; and L3 is located −381700 km from Earth's center, which is 99.3% of the Earth–Moon distance or 0.7084% in front of the Moon's 'negative' position.
| Body pair | Semimajor axis, SMA (×109 m) | L1 (×109 m) | 1 − L1/SMA (%) | L2 (×109 m) | L2/SMA − 1 (%) | L3 (×109 m) | 1 + L3/SMA (%) |
|---|---|---|---|---|---|---|---|
| Earth–Moon | 0.3844 | 0.32639 | 15.09 | 0.4489 | 16.78 | −0.38168 | 0.7084 |
| Sun–Mercury | 57.909 | 57.689 | 0.3806 | 58.13 | 0.3815 | −57.909 | 0.000009683 |
| Sun–Venus | 108.21 | 107.2 | 0.9315 | 109.22 | 0.9373 | −108.21 | 0.0001428 |
| Sun–Earth | 149.6 | 148.11 | 0.997 | 151.1 | 1.004 | −149.6 | 0.0001752 |
| Sun–Mars | 227.94 | 226.86 | 0.4748 | 229.03 | 0.4763 | −227.94 | 0.00001882 |
| Sun–Jupiter | 778.34 | 726.45 | 6.667 | 832.65 | 6.978 | −777.91 | 0.05563 |
| Sun–Saturn | 1426.7 | 1362.5 | 4.496 | 1492.8 | 4.635 | −1426.4 | 0.01667 |
| Sun–Uranus | 2870.7 | 2801.1 | 2.421 | 2941.3 | 2.461 | −2870.6 | 0.002546 |
| Sun–Neptune | 4498.4 | 4383.4 | 2.557 | 4615.4 | 2.602 | −4498.3 | 0.003004 |
Spaceflight applications
Sun–Earth
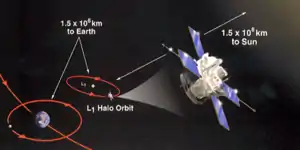
Sun–Earth L1 is suited for making observations of the Sun–Earth system. Objects here are never shadowed by Earth or the Moon and, if observing Earth, always view the sunlit hemisphere. The first mission of this type was the 1978 International Sun Earth Explorer 3 (ISEE-3) mission used as an interplanetary early warning storm monitor for solar disturbances.[23] Since June 2015, DSCOVR has orbited the L1 point. Conversely it is also useful for space-based solar telescopes, because it provides an uninterrupted view of the Sun and any space weather (including the solar wind and coronal mass ejections) reaches L1 up to an hour before Earth. Solar and heliospheric missions currently located around L1 include the Solar and Heliospheric Observatory, Wind, and the Advanced Composition Explorer. Planned missions include the Interstellar Mapping and Acceleration Probe (IMAP) and the NEO Surveyor.
Sun–Earth L2 is a good spot for space-based observatories. Because an object around L2 will maintain the same relative position with respect to the Sun and Earth, shielding and calibration are much simpler. It is, however, slightly beyond the reach of Earth's umbra,[24] so solar radiation is not completely blocked at L2. Spacecraft generally orbit around L2, avoiding partial eclipses of the Sun to maintain a constant temperature. From locations near L2, the Sun, Earth and Moon are relatively close together in the sky; this means that a large sunshade with the telescope on the dark-side can allow the telescope to cool passively to around 50 K – this is especially helpful for infrared astronomy and observations of the cosmic microwave background. The James Webb Space Telescope was positioned in a halo orbit about L2 on January 24, 2022.
Sun–Earth L1 and L2 are saddle points and exponentially unstable with time constant of roughly 23 days. Satellites at these points will wander off in a few months unless course corrections are made.[8]
Sun–Earth L3 was a popular place to put a "Counter-Earth" in pulp science fiction and comic books, despite the fact that the existence of a planetary body in this location had been understood as an impossibility once orbital mechanics and the perturbations of planets upon each other's orbits came to be understood, long before the Space Age; the influence of an Earth-sized body on other planets would not have gone undetected, nor would the fact that the foci of Earth's orbital ellipse would not have been in their expected places, due to the mass of the counter-Earth. The Sun–Earth L3, however, is a weak saddle point and exponentially unstable with time constant of roughly 150 years.[8] Moreover, it could not contain a natural object, large or small, for very long because the gravitational forces of the other planets are stronger than that of Earth (for example, Venus comes within 0.3 AU of this L3 every 20 months).
A spacecraft orbiting near Sun–Earth L3 would be able to closely monitor the evolution of active sunspot regions before they rotate into a geoeffective position, so that a seven-day early warning could be issued by the NOAA Space Weather Prediction Center. Moreover, a satellite near Sun–Earth L3 would provide very important observations not only for Earth forecasts, but also for deep space support (Mars predictions and for crewed mission to near-Earth asteroids). In 2010, spacecraft transfer trajectories to Sun–Earth L3 were studied and several designs were considered.[25]
Earth–Moon
Earth–Moon L1 allows comparatively easy access to Lunar and Earth orbits with minimal change in velocity and this has as an advantage to position a habitable space station intended to help transport cargo and personnel to the Moon and back.
Earth–Moon L2 has been used for a communications satellite covering the Moon's far side, for example, Queqiao, launched in 2018,[26] and would be "an ideal location" for a propellant depot as part of the proposed depot-based space transportation architecture.[27]
Sun–Venus
Scientists at the B612 Foundation were[28] planning to use Venus's L3 point to position their planned Sentinel telescope, which aimed to look back towards Earth's orbit and compile a catalogue of near-Earth asteroids.[29]
Sun–Mars
In 2017, the idea of positioning a magnetic dipole shield at the Sun–Mars L1 point for use as an artificial magnetosphere for Mars was discussed at a NASA conference.[30] The idea is that this would protect the planet's atmosphere from the Sun's radiation and solar winds.
See also
- Co-orbital configuration
- Euler's three-body problem
- Gegenschein
- Klemperer rosette
- L5 Society
- Lagrange point colonization
- Lagrangian mechanics
- List of objects at Lagrange points
- Lunar space elevator
- Oberth effect
References
- Cornish, Neil J. (1998). "The Lagrange Points" (PDF). WMAP Education and Outreach. Archived from the original (PDF) on September 7, 2015. Retrieved 15 Dec 2015.
- Weisstein, Eric. "Lagrange Points". Eric Weisstein's World of Physics.
- One Year on Earth – Seen From 1 Million Miles on YouTube
- Koon, W. S.; Lo, M. W.; Marsden, J. E.; Ross, S. D. (2006). Dynamical Systems, the Three-Body Problem, and Space Mission Design. p. 9. Archived from the original on 2008-05-27. Retrieved 2008-06-09. (16MB)
- Euler, Leonhard (1765). De motu rectilineo trium corporum se mutuo attrahentium (PDF).
- Lagrange, Joseph-Louis (1867–92). "Tome 6, Chapitre II: Essai sur le problème des trois corps". Œuvres de Lagrange (in French). Gauthier-Villars. pp. 229–334.
- "L2 Orbit". Space Telescope Science Institute. Archived from the original on 3 February 2014. Retrieved 28 August 2016.
- "The Lagrange Points" (PDF). NASA. 1998., Neil J. Cornish, with input from Jeremy Goodman
- Choi 2011-07-27T17:06:00Z, Charles Q. (27 July 2011). "First Asteroid Companion of Earth Discovered at Last". Space.com.
- "NASA - NASA's Wise Mission Finds First Trojan Asteroid Sharing Earth's Orbit". www.nasa.gov.
- Hui, Man-To; Wiegert, Paul A.; Tholen, David J.; Föhring, Dora (November 2021). "The Second Earth Trojan 2020 XL5". The Astrophysical Journal Letters. 922 (2): L25. arXiv:2111.05058. Bibcode:2021ApJ...922L..25H. doi:10.3847/2041-8213/ac37bf. S2CID 243860678.
- Slíz-Balogh, Judit; Barta, András; Horváth, Gábor (2018). "Celestial mechanics and polarization optics of the Kordylewski dust cloud in the Earth-Moon Lagrange point L5 - Part I. Three-dimensional celestial mechanical modelling of dust cloud formation". Monthly Notices of the Royal Astronomical Society. 480 (4): 5550–5559. arXiv:1910.07466. Bibcode:2018MNRAS.480.5550S. doi:10.1093/mnras/sty2049.
- Slíz-Balogh, Judit; Barta, András; Horváth, Gábor (2019). "Celestial mechanics and polarization optics of the Kordylewski dust cloud in the Earth-Moon Lagrange point L5. Part II. Imaging polarimetric observation: new evidence for the existence of Kordylewski dust cloud". Monthly Notices of the Royal Astronomical Society. 482 (1): 762–770. arXiv:1910.07471. Bibcode:2019MNRAS.482..762S. doi:10.1093/mnras/sty2630.
- Freitas, Robert; Valdes, Francisco (1980). "A Search for Natural or Artificial Objects Located at the Earth–Moon Libration Points". Icarus. 42 (3): 442–447. Bibcode:1980Icar...42..442F. doi:10.1016/0019-1035(80)90106-2.
- "List Of Neptune Trojans". Minor Planet Center. Archived from the original on 2011-07-25. Retrieved 2010-10-27.
- Belbruno, E.; Gott III, J. Richard (2005). "Where Did The Moon Come From?". The Astronomical Journal. 129 (3): 1724–1745. arXiv:astro-ph/0405372. Bibcode:2005AJ....129.1724B. doi:10.1086/427539. S2CID 12983980.
- Seidov, Zakir F. (March 1, 2004). "The Roche Problem: Some Analytics". The Astrophysical Journal. 603 (1): 283–284. arXiv:astro-ph/0311272. Bibcode:2004ApJ...603..283S. doi:10.1086/381315. S2CID 16724058.
- "Widnall, Lecture L18 - Exploring the Neighborhood: the Restricted Three-Body Problem" (PDF).
- Fitzpatrick, Richard. "Stability of Lagrange Points". Newtonian Dynamics. University of Texas.
- Greenspan, Thomas (January 7, 2014). "Stability of the Lagrange Points, L4 and L5" (PDF). Archived from the original (PDF) on April 18, 2018. Retrieved February 28, 2018.
- Pitjeva, E.V.; Standish, E.M. (2009-04-01). "Proposals for the masses of the three largest asteroids, the Moon-Earth mass ratio and the Astronomical Unit". Celestial Mechanics and Dynamical Astronomy. 103 (4): 365–372. Bibcode:2009CeMDA.103..365P. doi:10.1007/s10569-009-9203-8. S2CID 121374703.
- Cacolici, Gianna Nicole, et al., "Stability of Lagrange Points: James Webb Space Telescope", University of Arizona. Retrieved 17 Sept. 2018.
- "ISEE-3/ICE". Solar System Exploration. NASA. Archived from the original on July 20, 2015. Retrieved August 8, 2015.
- Angular size of the Sun at 1 AU + 1.5 million kilometres: 31.6′, angular size of Earth at 1.5 million kilometres: 29.3′
- Tantardini, Marco; Fantino, Elena; Ren, Yuan; Pergola, Pierpaolo; Gómez, Gerard; Masdemont, Josep J. (2010). "Spacecraft trajectories to the L3 point of the Sun–Earth three-body problem" (PDF). Celestial Mechanics and Dynamical Astronomy. 108 (3): 215–232. Bibcode:2010CeMDA.108..215T. doi:10.1007/s10569-010-9299-x. S2CID 121179935.
- Jones, Andrew (2018-06-14). "Chang'e-4 relay satellite enters halo orbit around Earth-Moon L2, microsatellite in lunar orbit". SpaceNews.
- Zegler, Frank; Kutter, Bernard (2010-09-02). "Evolving to a Depot-Based Space Transportation Architecture" (PDF). AIAA SPACE 2010 Conference & Exposition. AIAA. p. 4. Archived from the original (PDF) on 2014-06-24. Retrieved 2011-01-25.
L2 is in deep space far away from any planetary surface and hence the thermal, micrometeoroid, and atomic oxygen environments are vastly superior to those in LEO. Thermodynamic stasis and extended hardware life are far easier to obtain without these punishing conditions seen in LEO. L2 is not just a great gateway—it is a great place to store propellants. ... L2 is an ideal location to store propellants and cargos: it is close, high energy, and cold. More importantly, it allows the continuous onward movement of propellants from LEO depots, thus suppressing their size and effectively minimizing the near-Earth boiloff penalties.
- "B612 studying smallsat missions to search for near Earth objects". SpaceNews.com. June 20, 2017.
- "The Sentinel Mission". B612 Foundation. Archived from the original on 30 June 2012. Retrieved 1 February 2014.
- "NASA proposes a magnetic shield to protect Mars' atmosphere". phys.org.
External links
- Joseph-Louis, Comte Lagrange, from Oeuvres Tome 6, "Essai sur le Problème des Trois Corps"—Essai (PDF); source Tome 6 (Viewer)
- "Essay on the Three-Body Problem" by J-L Lagrange, translated from the above, in merlyn.demon.co.uk.
- Considerationes de motu corporum coelestium—Leonhard Euler—transcription and translation at merlyn.demon.co.uk.
- What are Lagrange points?—European Space Agency page, with good animations
- Explanation of Lagrange points—Prof. Neil J. Cornish
- A NASA explanation—also attributed to Neil J. Cornish
- Explanation of Lagrange points—Prof. John Baez
- Geometry and calculations of Lagrange points—Dr J R Stockton
- Locations of Lagrange points, with approximations—Dr. David Peter Stern
- An online calculator to compute the precise positions of the 5 Lagrange points for any 2-body system—Tony Dunn
- Astronomy Cast—Ep. 76: "Lagrange Points" by Fraser Cain and Dr. Pamela Gay
- The Five Points of Lagrange by Neil deGrasse Tyson
- Earth, a lone Trojan discovered
- See the Lagrange Points and Halo Orbits subsection under the section on Geosynchronous Transfer Orbit in NASA: Basics of Space Flight, Chapter 5