Munsell color system

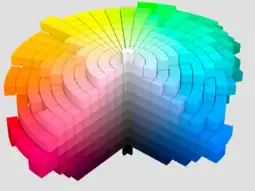
In colorimetry, the Munsell color system is a color space that specifies colors based on three properties of color: hue (basic color), chroma (color intensity), and value (lightness). It was created by Professor Albert H. Munsell in the first decade of the 20th century and adopted by the United States Department of Agriculture (USDA) as the official color system for soil research in the 1930s.

The Munsell color system, showing: a circle of hues at value 5 chroma 6; the neutral values from 0 to 10; and the chromas of purple-blue (5PB) at value 5.

Several earlier color order systems had placed colors into a three-dimensional color solid of one form or another, but Munsell was the first to separate hue, value, and chroma into perceptually uniform and independent dimensions, and he was the first to illustrate the colors systematically in three-dimensional space.[1] Munsell's system, particularly the later renotations, is based on rigorous measurements of human subjects' visual responses to color, putting it on a firm experimental scientific basis. Because of this basis in human visual perception, Munsell's system has outlasted its contemporary color models, and though it has been superseded for some uses by models such as CIELAB (L*a*b*) and CIECAM02, it is still in wide use today.[2]

Explanation
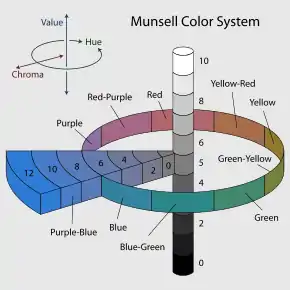
Munsell’s color sphere, 1900. Later, Munsell discovered that if hue, value, and chroma were to be kept perceptually uniform, achievable surface colors could not be forced into a regular geometric shape.
Three-dimensional representation of the 1943 Munsell renotations (with portion cut away). Notice the irregularity of the shape when compared with Munsell's earlier color sphere.

The system consists of three independent properties of color which can be represented cylindrically in three dimensions as an irregular color solid:

  • hue, measured by degrees around horizontal circles
  • chroma, measured radially outward from the neutral (gray) vertical axis
  • value, measured vertically on the core cylinder from 0 (black) to 10 (white)

Munsell determined the spacing of colors along these dimensions by taking measurements of human visual responses. In each dimension, Munsell colors are as close to perceptually uniform as he could make them, which makes the resulting shape quite irregular. As Munsell explains:

Desire to fit a chosen contour, such as the pyramid, cone, cylinder or cube, coupled with a lack of proper tests, has led to many distorted statements of color relations, and it becomes evident, when physical measurement of pigment values and chromas is studied, that no regular contour will serve.

— Albert H. Munsell, “A Pigment Color System and Notation”[3]

Hue

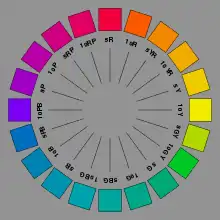
Each horizontal circle Munsell divided into five principal hues: Red, Yellow, Green, Blue, and Purple, along with 5 intermediate hues (e.g., YR) halfway between adjacent principal hues.[4] Each of these 10 steps, with the named hue given number 5, is then broken into 10 sub-steps, so that 100 hues are given integer values. In practice, color charts conventionally specify 40 hues, in increments of 2.5, progressing as for example 10R to 2.5YR.

Two colors of equal value and chroma, on opposite sides of a hue circle, are complementary colors, and mix additively to the neutral gray of the same value. The diagram below shows 40 evenly spaced Munsell hues, with complements vertically aligned.

Munsell hues; value 6 / chroma 6
5R
|
 5YR
|
 5Y
|
 5GY
|
 5G
|
 5BG
|
201 130 134
201 130 127
201 131 118
200 133 109
197 135 100
193 137 94
187 140 86
181 143 79
173 146 75
167 149 72
160 151 73
151 154 78
141 156 85
127 159 98
115 160 110
101 162 124
92 163 134
87 163 141
82 163 148
78 163 154
73 163 162
5BG
|
 5B
|
 5PB
|
 5P
|
 5RP
|
 5R
|
73 163 162
70 162 170
70 161 177
73 160 184
82 158 189
93 156 193
104 154 195
117 151 197
128 149 198
141 145 198
152 142 196
160 140 193
168 138 189
177 135 182
183 134 176
188 132 169
193 131 160
196 130 153
198 130 146
200 130 140
201 130 134

Value

Value, or lightness, varies vertically along the color solid, from black (value 0) at the bottom, to white (value 10) at the top.[5] Neutral grays lie along the vertical axis between black and white.

Several color solids before Munsell's plotted luminosity from black on the bottom to white on the top, with a gray gradient between them, but these systems neglected to keep perceptual lightness constant across horizontal slices. Instead, they plotted fully saturated yellow (light), and fully saturated blue and purple (dark) along the equator.

Chroma

Chroma, measured radially from the center of each slice, represents the “purity” of a color (related to saturation), with lower chroma being less pure (more washed out, as in pastels).[6] Note that there is no intrinsic upper limit to chroma. Different areas of the color space have different maximal chroma coordinates. For instance light yellow colors have considerably more potential chroma than light purples, due to the nature of the eye and the physics of color stimuli. This led to a wide range of possible chroma levels—up to the high 30s for some hue–value combinations (though it is difficult or impossible to make physical objects in colors of such high chromas, and they cannot be reproduced on current computer displays). Vivid solid colors are in the range of approximately 8.

Specifying a color

A color is fully specified by listing the three numbers for hue, value, and chroma in that order. For instance, a purple of medium lightness and fairly saturated would be 5P 5/10 with 5P meaning the color in the middle of the purple hue band, 5/ meaning medium value (lightness), and a chroma of 10 (see swatch). An achromatic color is specified by the syntax N V/. For example, a medium grey is specified by "N 5/".

In computer processing, the Munsell colors are converted to a set of "HVC" numbers. The V and C are the same as the normal chroma and value. The H (hue) number is converted by mapping the hue rings into numbers between 0 and 100, where both 0 and 100 correspond to 10RP.[7]

As the Munsell books, including the 1943 renotation, only contains colors for some points in the Munsell space, it is non-trivial to specify an arbitrary color in Munsell space. Interpolation must be used to assign meanings to non-book colors such as "2.8Y 6.95/2.3", followed by an inversion of the fitted Munsell-to-xyY transform. The ASTM has defined a method in 2008, but Centore 2012 is known to work better.[8]

History and influence
Runge's Farbenkugel (Color Sphere), 1810[lower-alpha 1]
Professor Albert H. Munsell
Several editions of the Munsell Book of Color. The atlas is arranged into removable pages of color swatches of varying value and chroma for each of 40 particular hues.

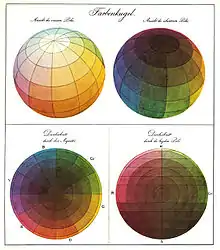
The idea of using a three-dimensional color solid to represent all colors was developed during the 18th and 19th centuries. Several different shapes for such a solid were proposed, including: a double triangular pyramid by Tobias Mayer in 1758, a single triangular pyramid by Johann Heinrich Lambert in 1772, a sphere by Philipp Otto Runge in 1810, a hemisphere by Michel Eugène Chevreul in 1839, a cone by Hermann von Helmholtz in 1860, a tilted cube by William Benson in 1868, and a slanted double cone by August Kirschmann in 1895.[9] These systems became progressively more sophisticated, with Kirschmann’s even recognizing the difference in value between bright colors of different hues. But all of them remained either purely theoretical or encountered practical problems in accommodating all colors. Furthermore, none was based on any rigorous scientific measurement of human vision; before Munsell, the relationship between hue, value, and chroma was not understood.[9]

Twenty hues of the Munsell color system at maximum chroma to stay in the sRGB gamut.

Albert Munsell, an artist and professor of art at the Massachusetts Normal Art School (now Massachusetts College of Art and Design, or MassArt), wanted to create a "rational way to describe color" that would use decimal notation instead of color names (which he felt were "foolish" and "misleading"),[10] which he could use to teach his students about color. He first started work on the system in 1898 and published it in full form in A Color Notation in 1905.

The original embodiment of the system (the 1905 Atlas) had some deficiencies as a physical representation of the theoretical system. These were improved significantly in the 1929 Munsell Book of Color and through an extensive series of experiments carried out by the Optical Society of America in the 1940s resulting in the notations (sample definitions) for the modern Munsell Book of Color. Though several replacements for the Munsell system have been invented, building on Munsell's foundational ideas—including the Optical Society of America's Uniform Color Scales, and the International Commission on Illumination’s CIELAB (L*a*b*) and CIECAM02 color models—the Munsell system is still widely used, by, among others, ANSI to define skin and hair colors for forensic pathology, the USGS for matching soil colors, in prosthodontics during the selection of shades for dental restorations, and breweries for matching beer colors.[11][12][lower-alpha 2]

The original Munsell color chart remains useful for comparing computer models of human color vision.[13]

See also
  • Natural Color System

Notes
  1. There are mathematical issues with this depiction: If one calls the concentric rings "chroma" and the horizontal stripes "lightness", then it is not possible to have a color whose "chroma" is 2 (counting from the center outward) and "lightness" is 9 (counting from the bottom to the top). This means that each color cannot be uniquely identified by a single set of "hue", "lightness" and "chroma" values. Albert Munsell's color sphere was designed in such a way as to avoid this pitfall, however.
  2. Beer color is measured in Degrees Lovibond, a metric based on the Munsell system

References
  1. Kuehni (2002), p. 21
  2. Landa (2005), pp. 437–438 Archived 2017-04-30 at the Wayback Machine,
  3. Munsell (1912), p. 239
  4. Cleland (1921), Ch. 1
  5. Cleland (1921), Ch. 2
  6. Cleland (1921), Ch. 3
  7. ASTM, Standard D 1535-08, "Standard Practice for Specifying Color by the Munsell System," approved January 1, 2008.
  8. Centore, Paul (December 2012). "An open-source inversion algorithm for the Munsell renotation". Color Research & Application. 37 (6): 455–464. doi:10.1002/col.20715.
  9. Kuenhi (2002), pp. 20–21
  10. (Munsell 1905), ch.1, pg. 7
  11. MacEvoy (2005)
  12. Landa (2005), pp. 442–443.
  13. "A perceptual color space for image processing".

Bibliography
  • Cleland, Thomas M. (1921). A practical description of the Munsell color system, with suggestions for its use. Boston: Munsell Color Company. One of the first books about the Munsell color system, explaining the intuition behind its three dimensions, and suggesting possible uses of the system in picking color combinations. An edited version can be found at http://www.applepainter.com/.
  • Kuehni, Rolf G. (February 2002). "The early development of the Munsell system". Color Research and Application. 27 (1): 20–27. doi:10.1002/col.10002. A description of color systems leading up to Munsell's, and a biographical explanation of Munsell's changing ideas about color and development of his color solid, leading up to the publication of A Color Notation in 1905.
  • Landa, Edward R.; Fairchild, Mark D. (September–October 2005). "Charting Color from the Eye of the Beholder" (PDF). American Scientist. 93 (5): 436–443. CiteSeerX 10.1.1.77.9634. doi:10.1511/2005.5.436. An introductory explanation of the development and influence of the Munsell system.
  • MacEvoy, Bruce (2005-08-01). "Modern Color Models – Munsell Color System". Color Vision. Retrieved 2007-04-16. A concise introduction to the Munsell color system, on a web page which also discusses several other color systems, putting the Munsell system in its historical context.
  • Munsell, Albert H. (1905). A Color Notation. Boston: G. H. Ellis Co. Munsell's original description of his system. A Color Notation was published before he had established the irregular shape of a perceptual color solid, so it describes colors positioned in a sphere.
  • Munsell, Albert H. (January 1912). "A Pigment Color System and Notation". The American Journal of Psychology. 23 (2): 236–244. doi:10.2307/1412843. JSTOR 1412843. Munsell's description of his color system, from a lecture to the American Psychological Association.
  • Nickerson, Dorothy (1976). "History of the Munsell color system, company, and foundation". Color Research and Application. 1 (1): 7–10.

General information:

  • Munsell.com, the homepage of Munsell Color, a subdivision of X-Rite, current owners of the Munsell Color Company.
    • Munsell page at the X-Rite website.
  • ApplePainter.com, a site explaining the Munsell color chart, including an edited version of Cleland's book, A practical description of the Munsell color system.
  • An explanation of the Munsell system at Adobe.com. Retrieved 13 August 2003
  • A brief explanation at the site of the Japanese company Dainichiseika Color & Chemicals, including a nice diagram of the Munsell color solid.

Data and conversion:

Other tools:

  • ToyPalette from Loo & Cox, a web application for generating color palettes from images. Munsell color analysis of digital image.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.