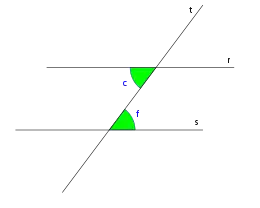Ángulos entre paralelas

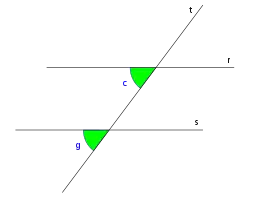
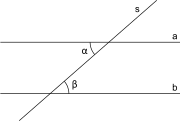
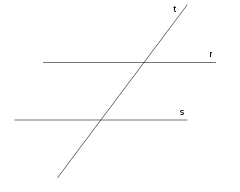
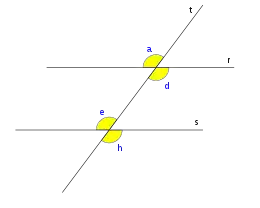
Los ángulos entre rectas paralelas y una secante, en geometría euclidiana, son los ocho ángulos formados por dos rectas paralelas (r y s en la imagen de la derecha) y una transversal a ellas (t).

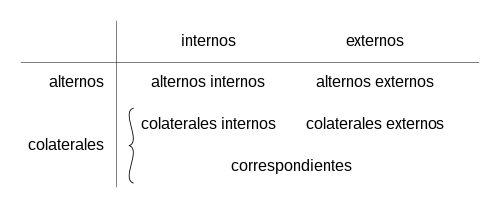
Denominación
  • Ángulos alternos: son los que se encuentran a distinto lado de la secante.
  • Ángulos colaterales: son los que se encuentran al mismo lado de la secante.
  • Alternos internos: son los que se encuentran en la zona interior de las rectas paralelas.
  • Alternos externos: Son los que se encuentran en la zona externa de las rectas paralelas.
  • Correspondientes: Son los que se encuentran a un mismo lado de la secante, uno es externo y el otro interno.

Ángulos alternos internos

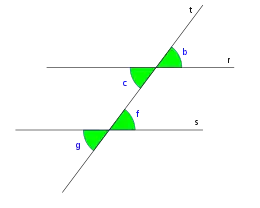
Las parejas de ángulos: c,f; d,e se llaman ángulos alternos internos.

Los ángulos alternos internos son congruentes. Pasa por el vértice opuesto en lo que podemos ver esto se suma por la distancia de las líneas paralelas en ciertos casos el ángulo de un triángulo mide 180° grados y para cada ángulo siempre se busca que 35° o alguna otra cifra sumados den 180°.

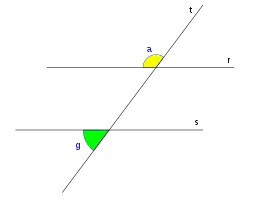
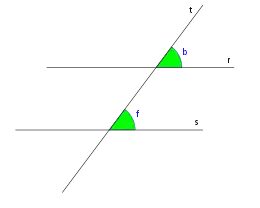
Ángulos alternos externos

Las parejas de ángulos: a,h; se llaman ángulos alternos externos.

Los ángulos alternos externos son congruentes.

Ángulos colaterales internos

Los ángulos colaterales internos[1] o conjugados internos[2] son los que se encuentran del mismo lado de la secante y entre de las rectas paralelas.

Son ángulos colaterales internos los siguientes ángulos: c,e; d,f.

Los ángulos conjugados internos son suplementarios (suman ).

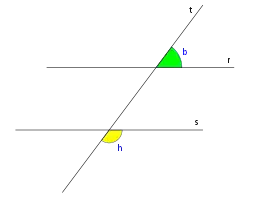
Ángulos colaterales externos

Los ángulos colaterales externos[1] o conjugados externos son los que se encuentran al mismo lado de la secante y en la parte exterior de las rectas paralelas.

Son ángulos colaterales externos los siguientes ángulos: a,g; b,h.

Los ángulos colaterales son suplementarios (suman ).

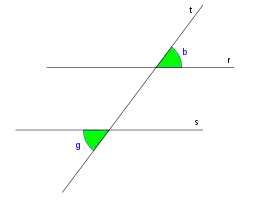
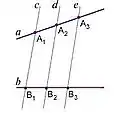
Ángulos correspondientes

Son los ángulos que se encuentran a un mismo lado de la secante, uno es externo y el otro interno, pero no son adyacentes. Los pares de ángulos: c, g; a, e; d, h y b, f; son correspondientes

Los ángulos correspondientes son congruentes.

Ángulos congruentes entre paralelas

Los ángulos opuestos por el vértice son congruentes, de modo que, de los ocho ángulos formados entre dos paralelas y una transversal, hay únicamente dos distintos, que no son adyacentes.

Teoremas y resultados relacionados

La noción de ángulos correspondientes es la base de numerosos ejemplos y teoremas fundamentales de la geometría,[3] presente en los cursos de enseñanza media de las matemáticas.[Ver: Bibliografía] Es un resultado geométrico intuitivo conocido y manejado desde la antigüedad, de manera tanto práctica como teórica,[4] si bien es la ciencia griega, y en particular Euclides, en los Elementos (siglo III a.C.), quienes formalizan los conceptos y las nociones de un modo que ha permanecido casi sin variaciones hasta nuestros días.

Según cuenta la leyenda, el filósofo Tales de Mileto utilizó esta propiedad para medir la altura de las pirámides de Guiza, alrededor del año 500 a. C.


Proposiciones de Euclides

La controversia sobre el V postulado alcanza la definición de los ángulos entre rectas paralelas y una secante desde el momento mismo de la elección de la noción de «rectas paralelas»: las que guardan siempre la misma distancia; las que no se encuentran; o bien las que forman ángulos congruentes al ser cortadas por una transversal.[5]

De Los Elementos de Euclides:

Proposición 28

Si un segmento al incidir sobre dos rectas hace el ángulo externo igual al interno y opuesto del mismo lado, o los dos internos del mismo lado iguales a dos ángulos rectos, las rectas serán paralelas entre sí.

Proposición 29

Una recta que corta a otras dos rectas paralelas hace los ángulos alternos iguales, los ángulos externos iguales a los interiores y opuestos, y la suma de los ángulos internos por el mismo lado iguales a dos rectos.

Definición 23

Rectas paralelas son aquellas que, estando en un mismo plano y siendo prolongadas indefinidamente en ambos sentidos, no se encuentran una a otra en ninguno de ellos.

Independencia del V postulado
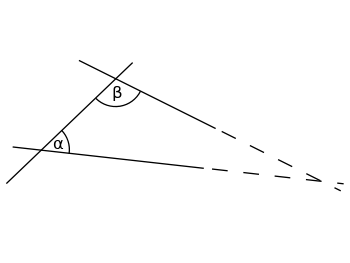
Si los ángulos interiores α y β no son suplementarios, las rectas prolongadas se intersecan (véase: Quinto postulado de Euclides).

Los siguientes dos resultados (lógicamente equivalentes[6]) son independientes del V postulado de Euclides. La Proposición 16, por ejemplo, no se cumple en geometría elíptica.

De Los Elementos de Euclides:

Proposición 27

Si un segmento al incidir sobre dos rectas hace los ángulos alternos iguales entre sí, las dos rectas serán paralelas.

Proposición 16

En cualquier triángulo, si se alarga uno de los lados, el ángulo exterior es mayor o igual que el ángulo interior y los ángulos opuestos.

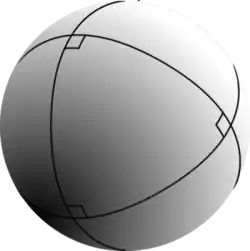
Geometría no-euclidiana

En la geometría absoluta o la geometría esférica por ejemplo, el quinto postulado de Euclides no aplica, por lo que los ángulos entre rectas paralelas y una secante tienen propiedades diferentes.

Contraejemplos
Geometría elíptica.
Geometría hiperbólica.
Disco de Poincaré.

Véase también
Relaciones aritméticas entre ángulos:
Relaciones posicionales entre ángulos:

Notas y referencias
  1. Toral Gutiérrez, Carlos (2005). Curso de Matemáticas 3º. Progreso. p. 26. ISBN 968-436-011-8.
  2. Matemáticas primer semestre. Grupo Tacaná. 2005. p. 109. ISBN 968-436-011-8.
  3. Ver: Regla y compás.
  4. Ver: Historia de la geometría.
  5. Manifiestamente, Euclides no utiliza el concepto en sus primeras 26 proposiciones.
  6. Heath, T.L., The thirteen books of Euclid's Elements, Vol.1, Dover, 1956, pg.309.

Bibliografía
  • Polania Sagra, Claudia Marcela; Sánchez Zuleta, Carmen Cecilia (2 de 2007). «3.2». Un acercamiento al pensamiento geométrico (1 edición). Lorenza Correa Restrepo. p. 141. ISBN 9789589812907.
  • Ibáñez Carrasco, Patricia; García Torres, Gerardo (6 de 2006). «1.4». Matemáticas II, Geometría Y Trigonometría (1 edición). Cengage Learning.
  • Landaverde, Felipe de Jesús (1977). Curso de Geometría. Editorial Progreso. p. 46. ISBN 9684361157.

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.