Árbol 2-3
En las ciencias de la computación, los árboles-2-3 son estructuras de datos de árbol que se encuentran comúnmente en las implementaciones de bases de datos y sistemas de archivos. Los árboles 2-3 mantienen los datos ordenados y las inserciones y eliminaciones se realizan en tiempo logarítmico amortizado.
Definición
Son un tipo de árbol balanceado por altura (height balanced). Se define como un árbol en dónde todos los nodos no-terminales tienen 2 o 3 descendientes y todos los nodos hoja tienen la misma longitud (path length) o distancia desde la raíz.
Fueron introducidos con el objetivo de mejorar el tiempo de acceso en estructuras de datos manejados en memoria secundaria, donde el número de consultas a un registro influye de manera determinante en el tiempo de respuesta de la operación.
La estructura de árbol 2-3 exige que el crecimiento no se haga a nivel de las hojas (aunque la inserción sigue siendo en las hojas), sino a nivel de la raíz, ya que todas las hojas se deben mantener siempre en el mismo nivel. El proceso global de inserción comienza por localizar la hoja en la cual se debe agregar el elemento.
Propiedades
Un árbol 2-3 permite que un nodo tenga dos o tres hijos. Esta característica le permite conservar el balanceo tras insertar o borrar elementos, por lo que el algoritmo de búsqueda es casi tan rápido como en un árbol de búsqueda de altura mínima. Por otro lado, es mucho más fácil de mantenerlo.
En un árbol 2-3, los nodos internos han de tener 2 ò 3 hijos y todas las hojas han de estar al mismo nivel. De forma recursiva se pueden definir como:
A es un árbol 2-3 de altura h si:
- A es un árbol vacío (un árbol 2-3 de altura 0), o
- A es de la forma (r, I, D), donde r es un nodo e I y D son árboles 2-3 de altura h − 1, o
- A es de la forma (r, I, C, D), donde r es un nodo e I, C y D son árboles 2-3 de altura h-1.
Para usar estos árboles de forma eficiente en las búsquedas, hay que introducir un orden entre los elementos por lo que un árbol A es un árbol 2-3 de búsqueda de altura h si:
- Todos los elementos de I son menores que r y todos los elementos de D son mayores que r.
- A es de la forma (r1, r2,I, C, D), donde r1 _ r2, I, Ac y D son árboles 2-3 de búsqueda de altura h-1 y todos los elementos de I son menores que r1, todos los elementos de C son mayores que r1 y menores que r2 y todos los elementos de D son mayores que r2.
Esta definición implica que el número de hijos de un nodo es siempre uno más que el número de elementos que contiene ese nodo. En el caso de las hojas se permiten uno o dos elementos en el nodo. Desde ahora nos referiremos a los árboles 2-3 de búsqueda simplemente como árboles 2-3.
La especificación del tipo ARBOL23 es muy similar a la de otros árboles con una diferencia que es la definición de tres operaciones generadoras en lugar de dos. arbolVacìo es la operación que genera un árbol sin elementos, como en los otros tipos y hay una operación, consArbol, que genera un árbol 2-3 cuya raíz tiene un solo elemento y dos hijos y otra, cons3Arbol, que genera un árbol 2-3 cuya raíz tiene dos elementos y tres hijos. Estas dos últimas operaciones son los generadores que se mantienen ocultos al usuario.
Inserción
A la hora de insertar un nuevo dato en un árbol 2-3 se hace de forma que se mantenga el equilibrio en el árbol. La capacidad de tener uno o dos elementos en cada nodo ayuda a conseguirlo.
Pseudo código de inserción en un árbol 2-3
Si el árbol está vacío
Entonces crea un nuevo nodo y colocar el en el lado izquierdo del nodo.
Si ya hay un elemento y existe espacio en el nodo hacer
Si r1 es menos que el elemento
Entonces el elemento 0 se coloca a la derecha.
Sino
Si r1 es mayor que el elemento entonces el elemento se coloca del lado izquierdo y r1 del lado derecho.
Sino
Si el nodo esta lleno se parte en dos nodos del mismo nivel, se crea un nuevo nodo
y se reparten los tres elementos (dos elementos del nodo y el nuevo elemento)
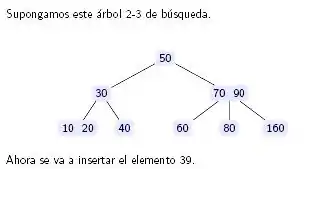
Ejemplos
A continuación se ofrecen ejemplos concretos para ilustrar el mecanismo de inserción:
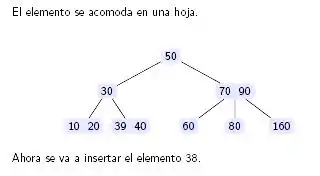
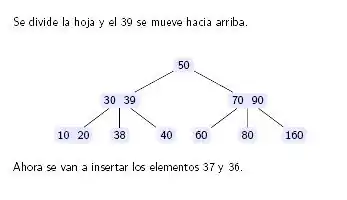
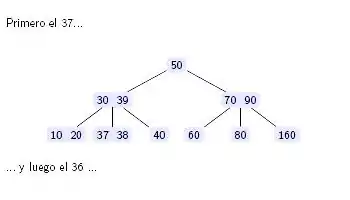
Especificación en C tipos
tipo_elmto = registro
clave:tipo_clave;
{los demás campos necesarios}
freg;
tipos_nodo = (hoja, interior);
nodo_dos_tres =
registro
clase:tipos_nodo;
selección
clase=hoja:(elmto:tipo_elmto);
clase=interior:(primer_hijo,segundo_hijo, tercer_hijo: diccionario;
menor_de_segundo, menor_de_tercero:tipo_clave)
fsel
freg
diccionario = ↑nodo_dos_tres
Inserción
algoritmo inserta1(e/s nodo:diccionario;
ent x:tipo_elmto; {x se insertará en el subárbol de nodo}
sal pt_nuevo:diccionario;
{puntero al nodo recién creado a la derecha de nodo}
sal menor:tipo_clave) {elmto más pequeño del subárbol al que apunta pt_nuevo}
programa principal :
principal
pt_nuevo:=nil;
si nodo es una hoja entonces
si x no es el elmto que está en nodo entonces
crea un nodo nuevo apuntado por pt_nuevo;
pone x en el nodo nuevo;
menor:=x.clave
fsi
sino {nodo es un nodo interno}
sea w el hijo de nodo a cuyo subárbol pertenece x;
inserta1(w, x,pt_atrás,menor_atrás);
si pt_atrás≠nil entonces
inserta el puntero pt_atrás entre los hijos de nodo justo a la derecha de w;
si nodo tiene cuatro hijos entonces
crea un nodo nuevo apuntado por pt_nuevo;
da al nuevo nodo los hijos 3º y 4º de nodo;
ajusta menor_de_segundo y menor_de_tercero en nodo y el nodo nuevo;
coloca menor como la menor clave entre los hijos del nodo nuevo
fsi
fsi
fsi
fin
Código en Maude :
eq insertar (E, arbolVacio) = consArbol (E, arbolVacio, arbolVacio) .
eq insertar (E, consArbol(E2, arbolVacio, arbolVacio)) =
if E < E2 then
cons3Arbol(E, E2, arbolVacio, arbolVacio, arbolVacio)
else
cons3Arbol(E2, E, arbolVacio, arbolVacio, arbolVacio)
fi .
eq insertar (E, cons3Arbol(E2, E3, arbolVacio, arbolVacio, arbolVacio)) =
consArbol (medio(E, E2, E3), consArbol (mínimo(E, E2), arbolVacio, arbolVacio),
consArbol (máximo(E, E3), arbolVacio, arbolVacio)) .
eq insertar (E, consArbol(E2, I, D)) =
if E < E2 then
equilibrar (consArbol(E2, insertar (E, I), D))
else
equilibrar (consArbol(E2, I, insertar (E, D)))
fi .
eq insertar (E, cons3Arbol(E2, E3, I, C, D)) =
if E < E2 then
equilibrar(cons3Arbol(E2, E3, insertar (E, I), C, D))
else
if E < E3 then
equilibrar(cons3Arbol(E2, E3, I, insertar (E, C), D))
else
equilibrar(cons3Arbol(E2, E3, I, C, insertar (E, D)))
fi
fi .
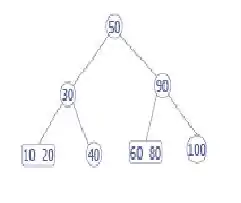
Ejemplo de eliminar :
Vamos a eliminar 65 de este árbol, 65 es un nodo interno, por lo que hay que dejarlo en la base.
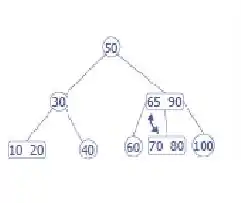
65 se encuentra ahora en una ubicación no válida, lo vamos a eliminar
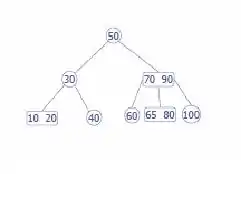
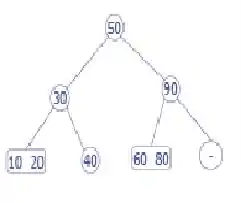
Ahora haremos lo mismo para eliminar 70 que es un nodo interno
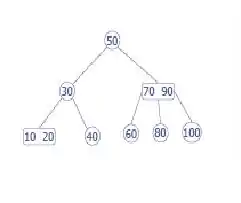
70 se encuentra ahora en una ubicación no válida, porque vamos a eliminarlo
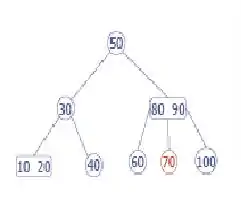
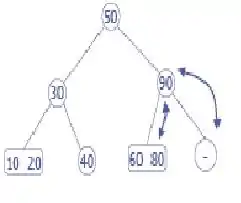
La eliminación de la hoja nos deja con un 2-3 árbol no valido
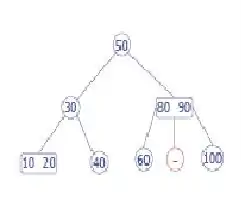
Combinar para fijar los nodos del árbol
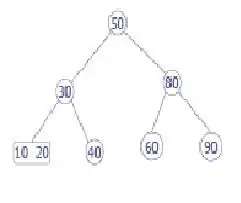
ahora eliminamos,100 es hoja ya se puede quitar
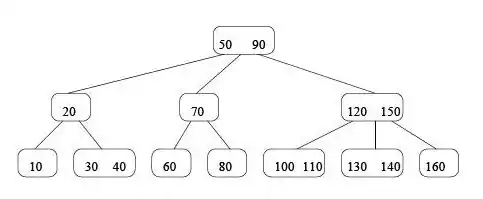
Árbol 2-3-4
Definición
Como una forma de eliminarlas búsquedas exhaustivas de los árboles binarios existen los árboles 2-3-4. Estos son árboles en cuyos nodos se permite tener más de una clave al mismo tiempo. Los árboles binarios tienen máximo 2 hijos (derecho e izquierdo). Si se le permite al nodo tener 2 valores, este podrá tener 3 ligas a subárboles y uno con 3 valores podrá tener 4 ligas. Un árbol con estas características puede contener entonces nodos con 2, 3 o 4 ligas, de ahí que se les llama árboles 2-3-4. En los árboles 2-3-4 todos los subárboles tienen la misma altura y están siempre balanceados. Estos árboles son muy atractivos para el almacenamiento y recuperación de claves, sin embargo son un tanto complicados de implementar. Operaciones básicas:
- Búsqueda (similar a los árboles multicamino de búsqueda)
- Inserción (se realiza en las hojas. Se pueden producir reestructuraciones del árbol)
- Borrado (se realiza en las hojas. Se pueden producir reestructuraciones del árbol)
Propiedades
- En un árbol 2-3-4 de altura h tenemos:
2h - 1 elementos si todos los nodos son del tipo 2-nodo 4h - 1 elementos si todos los nodos son del tipo 4-nodo por lo que la altura de un árbol 2-3-4 con n elementos se encuentra entre los límites: log4 (n+1) y log2 (n+1)
- Las reestructuraciones se realizan desde la raíz hacia las hojas
Inserción
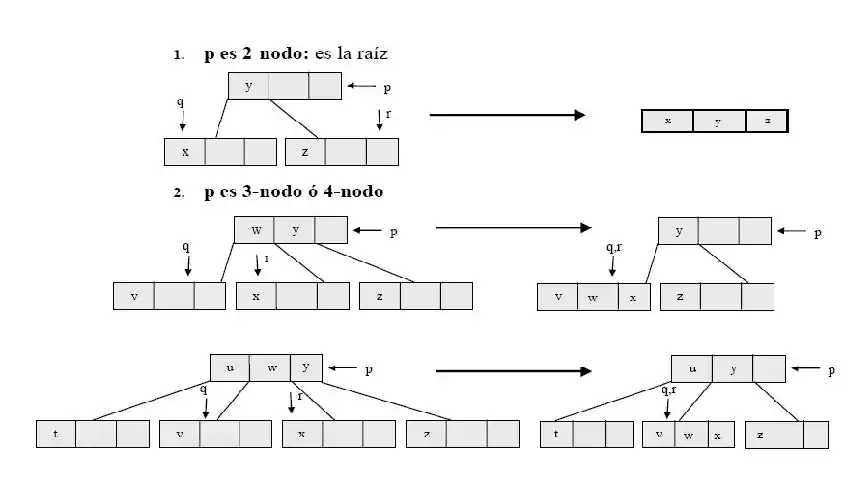
Existen 3 situaciones en las que se puede encontrar un 4-nodo:
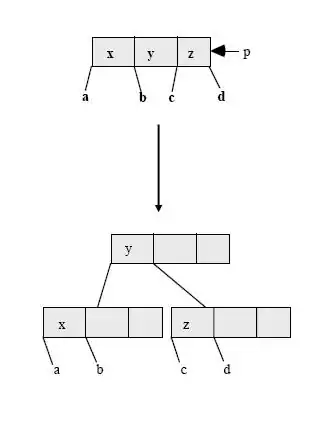
Es la raíz de un árbol 2-3-4:(DIVIDERAIZ (p))
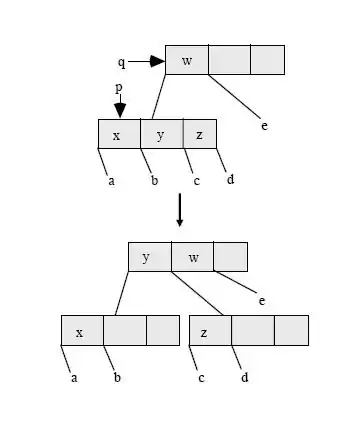
Su padre (q) es un 2-nodo(DIVIDEHIJODE2 (p, q) )
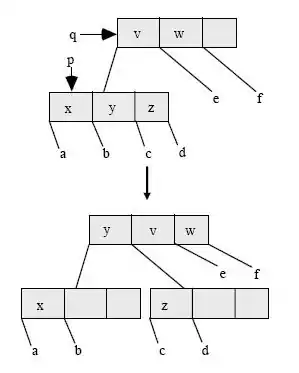
Su padre (q) es un 3-nodo:(DIVIDEHIJODE3 (p, q) )
Algoritmo de inserción
ALGORITMO insertar (A: TArb234, y: item)
VAR p, q: TNodo234*; noencontrado: Boolean; B: TArb234; FVAR
p = A.farb; q = p;
si EsVacío( A ) entonces A = ENRAIZAR (A, y, B)
sino
si p es 4-nodo entonces DIVIDERAIZ( A ) fsi
noencontrado = VERDADERO;
mientras noencontrado hacer
si p es 4-nodo entonces
si q es 2-nodo entonces DIVIDEHIJODE2( p, q );
sino DIVIDEHIJODE3( p, q ); fsi
p = q;
fsi
caso de COMPARAR( y, p ):
0:// Clave de y coincide con clave en p
ERROR, ETIQUETA EXISTENTE;
1:// p apunta a un nodo hoja
PONER( y, p ); noencontrado = FALSO;
2:// clave( y ) < ItemIz.clave( p )
q = p; p = p -> HiIz;
3:// ItemIz.clave (p)<clave (y)<ItemMe.clave (p)
q = p; p = p -> HiMeIz;
4://ItemMe.clave (p)<clave (y)<ItemDe.clave (p)
q = p; p = p-> HiMeDe;
5:// clave (y) > ItemDe.clave (p)
q = p; p = p -> HiDe;
fcaso
fmientras
fsi
fin
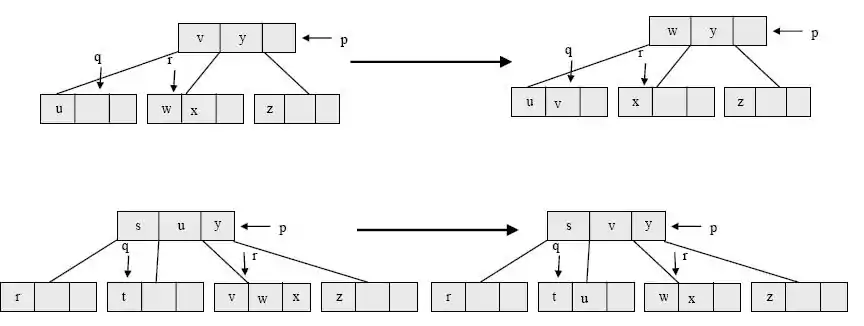
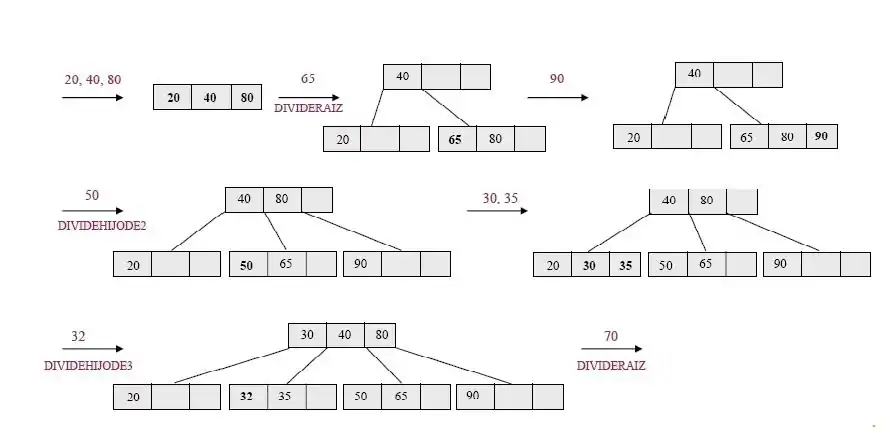
Ejemplo de insertar:
Borrar
- Se reduce al borrado de un elemento en una hoja
- En el movimiento de búsqueda, cuando pasemos a un nodo en el siguiente nivel, éste nodo debe ser 3-nodo ó 4-nodo; si no es así (es 2-nodo) hay que reestructurar.
p = nodo donde estamos q = siguiente nodo en la búsqueda r = uno de los nodos adyacentes a q (si hay dos adyacentes, escogemos r según criterio –hermano de la izquierda o hermano de la derecha–)
- Casos:
- . p es una hoja: p sólo puede ser 2-nodo si es la raíz
- . q es 3-nodo ó 4-nodo: la búsqueda continúa en q sin reestructurar.
- . q es 2-nodo y r es 2-nodo.