Árbol AVL
Un árbol AVL es un tipo especial de árbol binario ideado por los matemáticos soviéticos Adelson-Velskii y Landis. Fue el primer árbol de búsqueda binario auto-balanceable que se ideó.

Descripción
El árbol AVL toma su nombre de las iniciales de los apellidos de sus inventores, Georgii Adelson-Velskii y Yevgeniy Landis. Lo dieron a conocer en la publicación de un artículo en 1962, «An algorithm for the organization of information» («Un algoritmo para la organización de la información»).
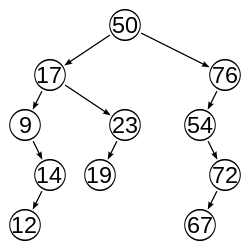
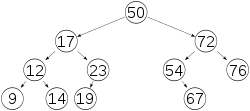
Los árboles AVL están siempre equilibrados de tal modo que para todos los nodos, la altura de la rama izquierda no difiere en más de una unidad de la altura de la rama derecha o viceversa. Gracias a esta forma de equilibrio (o balanceo), la complejidad de una búsqueda en uno de estos árboles se mantiene siempre en orden de complejidad O(log n). El factor de equilibrio puede ser almacenado directamente en cada nodo o ser computado a partir de las alturas de los subárboles.
Para conseguir esta propiedad de equilibrio, la inserción y el borrado de los nodos se ha de realizar de una forma especial. Si al realizar una operación de inserción o borrado se rompe la condición de equilibrio, hay que realizar una serie de rotaciones de los nodos.
Los árboles AVL más profundos son los árboles de Fibonacci.
Definición formal
Definición de la altura de un árbol
Sea un árbol binario de búsqueda y sean y sus subárboles, su altura , es:
- si el árbol contiene solo la raíz
- si contiene más nodos
Definición de árbol AVL
- Un árbol vacío es un árbol AVL
- Si es un árbol no vacío y y sus subárboles, entonces es AVL si y solo si:
- es AVL
- es AVL
Factor de equilibrio
Cada nodo, además de la información que se pretende almacenar, debe tener los dos punteros a los árboles derecho e izquierdo, igual que los árboles binarios de búsqueda (ABB), y además el dato que controla el factor de equilibrio.
El factor de equilibrio es la diferencia entre las alturas del árbol derecho y el izquierdo:
- FE = altura subárbol derecho - altura subárbol izquierdo
- Por definición, para un árbol AVL, este valor debe ser -1, 0 o 1.
Si el factor de equilibrio de un nodo es:
- 0 -> el nodo está equilibrado y sus subárboles tienen exactamente la misma altura.
- 1 -> el nodo está equilibrado y su subárbol derecho es un nivel más alto.
- -1 -> el nodo está equilibrado y su subárbol izquierdo es un nivel más alto.
Si el factor de equilibrio es necesario reequilibrar.
Operaciones
Las operaciones básicas de un árbol AVL implican generalmente el realizar los mismos algoritmos que serían realizados en un árbol binario de búsqueda desequilibrado, pero precedido o seguido por una o más de las llamadas "rotaciones AVL".
Rotaciones

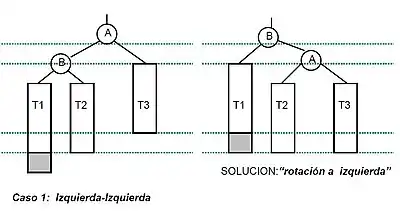
El reequilibrado se produce de abajo hacia arriba sobre los nodos en los que se produce el desequilibrio. Pueden darse dos casos: rotación simple o rotación doble; a su vez ambos casos pueden ser hacia la derecha o hacia la izquierda.
- Rotación simple a la derecha
De un árbol de raíz (r) y de hijos izquierdo (i) y derecho (d), lo que haremos será formar un nuevo árbol cuya raíz sea la raíz del hijo izquierdo, como hijo izquierdo colocamos el hijo izquierdo de i (nuestro i’) y como hijo derecho construimos un nuevo árbol que tendrá como raíz, la raíz del árbol (r), el hijo derecho de i (d’) será el hijo izquierdo y el hijo derecho será el hijo derecho del árbol (d).
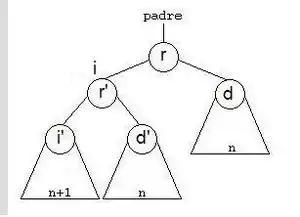
op rotDer: AVL{X} -> [AVL{X}] .
eq rotDer(arbolBin(R1, arbolBin(R2, I2, D2), D1)) ==
arbolBin(R2, I2, arbolBin(R1, D2, D)) .
- Rotación simple a la izquierda
De un árbol de raíz (r) y de hijos izquierdo (i) y derecho (d), consiste en formar un nuevo árbol cuya raíz sea la raíz del hijo derecho, como hijo derecho colocamos el hijo derecho de d (nuestro d’) y como hijo izquierdo construimos un nuevo árbol que tendrá como raíz la raíz del árbol (r), el hijo izquierdo de d será el hijo derecho (i’) de r y el hijo izquierdo será el hijo izquierdo del árbol (i).
Precondición : Tiene que tener hijo derecho no vacío.
op rotIzq: AVL{X} -> [AVL{X}] .
eq rotIzq(arbolBin(R1, I, arbolBin(R2, I2, D2))) ==
arbolBin(R2, arbolBin(R1, I, I2), D2) .
Si la inserción se produce en el hijo derecho del hijo izquierdo del nodo desequilibrado (o viceversa) hay que realizar una doble rotación.
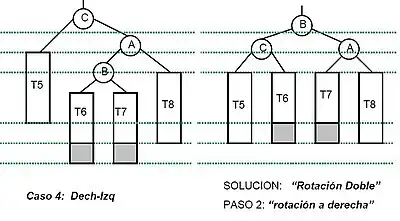
- Rotación doble a la derecha
La Rotación doble a la Derecha son dos rotaciones simples, primero rotación simple izquierda y luego rotación simple derecha.
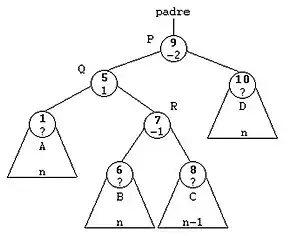
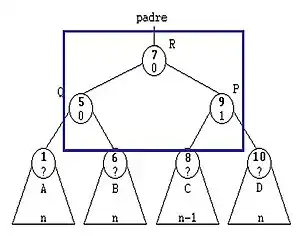
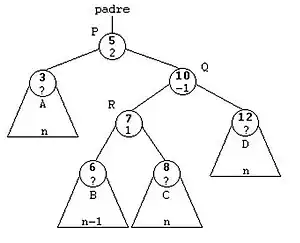
- Rotación doble a la izquierda
La Rotación doble a la Izquierda son dos rotaciones simples, primero rotación simple derecha y luego rotación simple izquierda.
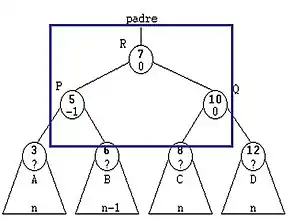
Inserción
La inserción en un árbol de AVL puede ser realizada insertando el valor dado en el árbol como si fuera un árbol de búsqueda binario desequilibrado y después retrocediendo hacia la raíz, rotando sobre cualquier nodo que pueda haberse desequilibrado durante la inserción.
Proceso de inserción:
- 1 Buscar hasta encontrar la posición de inserción o modificación (proceso idéntico a inserción en árbol binario de búsqueda)
- 2 Insertar el nuevo nodo con factor de equilibrio “equilibrado”
- 3 Desandar el camino de búsqueda, verificando el equilibrio de los nodos, y re-equilibrando si es necesario
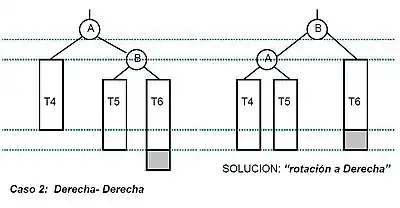
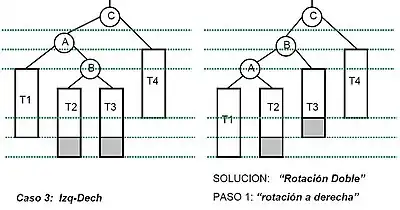
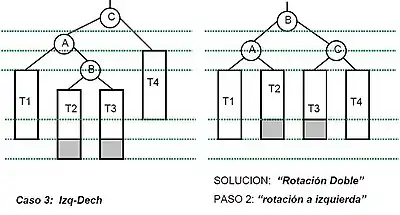
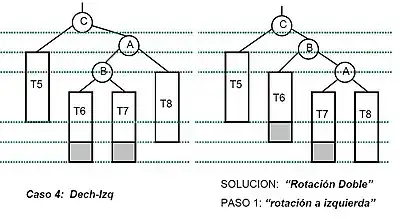
Debido a que las rotaciones son una operación que tienen complejidad constante y a que la altura está limitada a O (log(n)), el tiempo de ejecución para la inserción es del orden O (log(n)).
op insertar: X$Elt AVL{X} -> AVLNV{X} .
eq insertar(R, crear) == arbolBin(R, crear, crear) .
ceq insertar(R1, arbolBin(R2, I, D)) ==
if (R1==R2) then
arbolBin(R2, I, D)
elseif (R1<R2) then
if ( (altura(insertar(R1,I)) – altura(D)) < 2) then
arbolBin(R2, insertar(R1, I), D)
else ***hay que reequilibrar
if (R1 < raíz(I)) then
rotarDer(arbolBin(R2, insertar(R1, I), D))
else
rotarDer(arbolBin(R2, rotarIzq(insertar(R1, I)), D))
fi .
fi .
else
if ( (altura(insertar(R1,I)) – altura(D)) < 2) then
arbolBin(R2, insertar(R1, I), D)
else *** hay que reequilibrar
if (R1 > raíz(D)) then
rotarIzq(arbolBin(R, I, insertar(R1, D)))
else
rotatIzq(arbolBin(R, I, rotarDer(insertar(R1, D))))
fi .
fi .
fi .
Extracción
El procedimiento de borrado es el mismo que en el caso de árbol binario de búsqueda. La diferencia se encuentra en el proceso de reequilibrado posterior. El problema de la extracción puede resolverse en O (log(n)) pasos. Una extracción trae consigo una disminución de la altura de la rama donde se extrajo y tendrá como efecto un cambio en el factor de equilibrio del nodo padre de la rama en cuestión, pudiendo necesitarse una rotación.
Esta disminución de la altura y la corrección de los factores de equilibrio con sus posibles rotaciones asociadas pueden propagarse hasta la raíz.
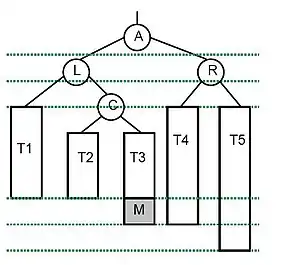 Borrar A, y la nueva raíz será M.
Borrar A, y la nueva raíz será M.
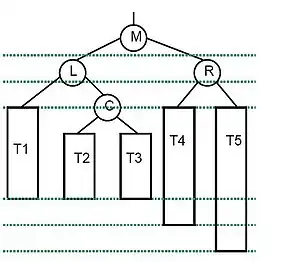 Borrado A, la nueva raíz es M. Aplicamos la rotación a la izquierda.
Borrado A, la nueva raíz es M. Aplicamos la rotación a la izquierda.
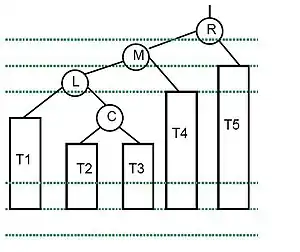 El árbol resultante ha perdido altura.
El árbol resultante ha perdido altura.
En el borrado pueden ser necesarias varias operaciones de restauración del equilibrio, y hay que seguir comprobando hasta llegar a la raíz.
op eliminar: X$Elt AVL{X} -> AVL{X} .
eq eliminar(R, crear) == crear .
ceq eliminar(R1, arbolBin(R2, I, D)) ==
if (R1 == R2) then
if esVacio(I) then
D
elseif esVacio(D) then
I
else
for (i=0; i<=2 i++)
if (altura(I) - altura(eliminar(min(D),D)) < 2) then
arbolBin(min(D), I, eliminar(min(D), D))
***tenemos que reequilibrar
elseif (altura(hijoIzq(I) >= altura(hijoDer(I)))) then
rotDer(arbolBin(min(D), I, eliminar(min(D),D)))
else
rotDer(arbolBin(min(D), rotIzq(I), eliminar(min(D),D)))
Búsqueda
Ejemplo en Java
public class Nodo {
int numMat;
Nodo izqda, drcha;
public Nodo(int mat){
numMat = mat;
izqda = drcha = null;
}
public void re_enorden(){
if(izqda != null)
izqda.re_enorden();
System.out.println("Matricula: " +numMat);
if(drcha != null)
drcha.re_enorden();
}
}
public class AVL {
private Nodo raíz;
public AVL (){
raíz = null;
}
public void insertar(int nuevoM){
if(raíz==null){
raíz = new Nodo(nuevoM);
}
else{
insertar(raíz,nuevoM);
}
}
private void insertar(Nodo rz, int nm){
if (rz == null)
rz = new Nodo(nm);
else if(nm < rz.numMat)
insertar(rz.izqda,nm);
else if(nm > rz.numMat)
insertar(rz.drcha,nm);
else
System.out.println("Numero Duplicados");
}
public void visualizar(){
if(raíz!=null)
raíz.re_enorden();
}
}
public class Ejecutar {
public static void main(String []args){
AVL árbol = new AVL ();
árbol.insertar(6);
árbol.insertar(3);
árbol.insertar(7);
árbol.visualizar();
}
}
Ejemplo de TAD AVL en C++
#include <cstdio>
struct AVL{
int dato, FB; // FB es la altura del subarbol izquierdo menos la altura del subarbol derecho
AVL *izq, *der;
bool borrado;
};
void rotarLL(AVL* &A){ //precond: el árbol necesita una rotacion LL
AVL* aux = A->izq->der;
A->izq->der = A;
A->izq->FB = 0;
AVL* aux2 = A->izq;
A->izq = aux;
A->FB = 0;
A = aux2;
}
void rotarRR(AVL* &A){ //precond: el árbol necesita una rotacion RR
AVL* aux = A->der->izq;
A->der->izq = A;
A->der->FB = 0;
AVL* aux2 = A->der;
A->der = aux;
A->FB = 0;
A = aux2;
}
void rotarLRalter(AVL* &A){ //precond: el árbol necesita una rotacion LR
rotarRR(A->izq);
rotarLL(A);
}
void rotarRLalter(AVL* &A){ //precond: el árbol necesita una rotacion RL
rotarLL(A->der);
rotarRR(A);
}
AVL* Crear(){
return NULL;
}
void Insert(int n, bool &aumento, AVL* &A){
if (A == NULL){
A = new AVL;
A->dato = n;
A->FB = 0;
A->izq = NULL;
A->der = NULL;
aumento = true;
A->borrado = false;
}else{
if (n < A->dato){
Insert(n, aumento, A->izq);
if (aumento){
switch (A->FB){
case -1:{
A->FB = 0;
aumento = false;
break;
}
case 0:{
A->FB = 1;
aumento = true;
break;
}
case 1:{
if (A->izq->FB == 1){ // Si es 1 necesita una rotacion LL si es -1 necesita una rotacion LR
rotarLL(A);
}else{
rotarLRalter(A);
}
aumento = false;
break;
}
}
}
}else{
Insert(n, aumento, A->der);
if (aumento){
switch (A->FB){
case -1:{
if (A->der->FB == 1){ // Si es 1 necesita una rotacion RL si es -1 necesita una rotacion RR
rotarRLalter(A);
}else{
rotarRR(A);
}
aumento = false;
break;
}
case 0:{
A->FB = -1;
aumento = true;
break;
}
case 1:{
A->FB = 0;
aumento = false;
break;
}
}
}
}
}
}
void Insertar(AVL* &A, int n){
bool aumento;
Insert(n, aumento, A);
}
bool EsVacio(AVL* A){
return A == NULL;
}
bool Pertenece(AVL* A, int n){
if (A == NULL){
return false;
}else{
if (A->dato == n){
if (A->borrado){
return false;
}else{
return true;
}
}else if (n < A->dato){
return Pertenece(A->izq, n);
}else{
return Pertenece(A->der, n);
}
}
}
void Borrar(AVL* &A, int n){
if (A->dato == n){
A->borrado = true;
}else if (n < A->dato){
Borrar(A->izq, n);
}else{
Borrar(A->der, n);
}
}