Árbol AA
En informática un árbol AA es un tipo de árbol binario de búsqueda auto-balanceable utilizado para almacenar y recuperar información ordenada de manera eficiente. Los árboles AA reciben el nombre de su inventor, Arne Andersson.
Los árboles AA son una variación del árbol rojo-negro, que a su vez es una mejora del árbol binario de búsqueda. A diferencia de los árboles rojo-negro, los nodos rojos en un árbol AA sólo pueden añadirse como un hijo derecho. En otras palabras, ningún nodo rojo puede ser un hijo izquierdo. De esta manera se simula un árbol 2-3 en lugar de un árbol 2-3-4, lo que simplifica las operaciones de mantenimiento. Los algoritmos de mantenimiento para un árbol rojo-negro necesitan considerar siete diferentes formas para balancear adecuadamente el árbol:

En un árbol AA, al cumplirse el estricto requisito de que sólo los enlaces derechos pueden ser rojos, sólo es necesario considerar dos formas:

Rotaciones de balanceo
En general, los árboles AA se implementan con la idea de un nivel en lugar de la de un color, a diferencia de los árboles rojo-negro. Cada nodo tiene un campo nivel y se deben cumplir las siguientes condiciones para que el árbol sea válido:
- El nivel de un nodo hoja es uno.
- El nivel de un hijo izquierdo es estrictamente menor que el de su padre.
- El nivel de un hijo derecho es menor o igual que el de su padre.
- El nivel de un nieto derecho es estrictamente menor que el de su abuelo.
- Cada nodo de nivel mayor que uno debe tener dos hijos.
Sólo se necesitan dos operaciones para mantener el equilibrio en un árbol AA. Estas operaciones se llaman torsión (skew) y división (split). La torsión es una rotación derecha que se realiza cuando una inserción o un borrado genera un enlace horizontal izquierdo, puede pensarse como un enlace rojo izquierdo en el contexto del árbol rojo-negro. La división es una rotación izquierda condicional que tiene lugar cuando una inserción o un borrado crea dos enlaces horizontales derechos, lo que de nuevo se corresponde con dos enlaces rojos consecutivos en el contexto de los árboles rojo-negro.
función torsión es
entrada: T, un nodo que representa un árbol AA que requiere ser rebalanceado.
salida: Otro nodo que representa el árbol AA rebalanceado.
si nil(T) entonces
devuelve Nil
si no si nivel(izquierda(T)) == nivel(T) entonces
Cambia los apuntadores de los enlaces horizontales a la izquierda.
L = izquierda(T)
izquierda(T) := derecha(L)
derecha(L) := T
devuelve L
si no
devuelve T
fin si
fin de la función
Torsión: 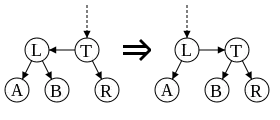
función división es
entrada: T, un nodo que representa un árbol AA que requiere ser rebalanceado.
salida: Otro nodo que representa el árbol AA rebalanceado.
si nil(T) entonces
devuelve Nil
si no si nivel(T) == nivel(derecha(derecha(T))) entonces
Tenemos dos enlaces horizontales a la derecha. Toma el de en medio, elévalo, y devuélvelo.
R = derecha(T)
derecha(T) := izquierda(R)
izquierda(R) := T
nivel(R) := nivel(R) + 1
devuelve R
si no
devuelve T
fin si
fin de la función
División: 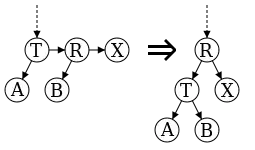
Inserción
La inserción comienza con la búsqueda normal en un árbol binario y su procedimiento de inserción. Después, a medida que se desenrolla la pila de llamadas, es fácil comprobar la validez del árbol y realizar las rotaciones que se precisen. Si aparece un enlace horizontal izquierdo, se realiza una torsión, y si aparecen dos enlaces horizontales derechos, se realiza una división, posiblemente incrementando el nivel del nuevo nodo raíz del subárbol correspondiente. Observe que el código de muestra realiza un incremento de nivel(T). Lo que hace necesario continuar comprobando la validez del árbol a medida que las modificaciones suben desde las hojas.
función insertar es
entrada: X, el valor a ser insertado, y T, la raíz del árbol en el cual se insertará.
salida: Una versión balanceada de T que incluye a X.
Haz el procedimiento normal de inserción de un árbol de búsqueda binario.
Asigna al hijo correcto el resultado de la llamada recursiva en caso de que
un nodo nuevo fue creado o la raíz del subárbol cambió.
si nil(T) entonces
Crea una nueva hoja con X.
devuelve nodo(X, 1, Nil, Nil)
si no si X < valor(T) entonces
izquierda(T) := insertar(X, izquierda(T))
si no si X > valor(T) entonces
derecha(T) := insertar(X, derecha(T))
fin si
Note que el caso X == valor(T) no está especificado. En esta implementación,
no tendrá ningún ejemplo. Se puede cambiar el comportamiento dependiendo de
la implementación.
Haz la torsión y luego la división. Las condiciones de si serán hechas ambas
acciones están dentro de los procedimientos ya descritos arriba.
T := torsión(T)
T := división(T)
devuelve T fin de la función
Borrado
Como en la mayoría de árboles binarios balanceados, el borrado de un nodo interno puede convertirse en el borrado de un nodo hoja al intercambiar el nodo interno bien con su predecesor o sucesor más próximo, dependiendo del que esté en el árbol o de los deseos del implementador. Para recuperar un predecesor simplemente se debe seguir un enlace izquierdo y después todos los enlaces derechos restantes. De forma similar, el sucesor se puede encontrar al ir una vez a la derecha y una vez a la izquierda hasta que se encuentre un puntero nulo. Dada la propiedad de los árboles AA de que todos los nodos de un nivel superior a uno tienen dos hijos, el nodo sucesor o predecesor tendrá nivel 1, haciendo que su eliminado sea trivial.
Para re-equilibrar un árbol existen diferentes aproximaciones. La que describió Andersson en su publicación original es la más simple, y se describirá aquí, aunque implementaciones reales pueden optar por un enfoque más optimizado. Tras un borrado, el primer paso para mantener la validez es reducir el nivel de todos los nodos cuyos hijos están dos niveles por debajo de ellos, o a los que les faltan hijos. Después, todo el nivel debe ser torsionado y dividido. Esta aproximación se ha visto favorecida por el hecho de que se basa en tres pasos independientes y fáciles de entender:
- Decrementar el nivel, si es necesario.
- Torsionar el nivel.
- Dividir el nivel.
Sin embargo, debemos torsionar y dividir todo el nivel en lugar de un solo nodo lo que complica nuestro código.
función borrar es
entrada: X, el valor a ser borrado, y T, la raíz del árbol del que se debe borrar.
salida: T, balanceado, sin el valor X.
si X > valor(T) entonces
derecha(T) := borrar(X, derecha(T))
si no si X < valor(T) entonces
izquierda(T) := borrar(X, izquierda(T))
si no
si somos una hoja es fácil, si no, hay que reducir ese caso.
si hoja(T) entonces
regresa Nil
si no si nil(izquierda(T)) entonces
L := sucesor(T)
derecha(T) := borrar(L, derecha(T))
valor(T) := L
si no
L := predecesor(T)
izquierda(T) := borrar(L, izquierda(T))
valor(T) := L
fin si
fin si
Rebalancea el árbol. Decrementa el nivel de los nodos en este nivel si es necesario, y
después torsiona y divide todos los nodos en el nuevo nivel.
T := decrementa_nivel(T)
T := torsión(T)
derecha(T) := torsión(derecha(T))
derecha(derecha(T)) := torsión(derecha(derecha(T)))
T := división(T)
derecha(T) := división(derecha(T))
regresa T
fin de la función
función decrementa_nivel es
entrada: T, un árbol del que queremos quitar enlaces que se saltan niveles.
salida: T con sus niveles decrementados.
debe_ser = min(nivel(izquierda(T)), nivel(derecha(T))) + 1
si debe_ser < nivel(T) entonces
nivel(T) := debe_ser
si debe_ser < nivel(derecha(T)) entonces
nivel(derecha(T)) := debe_ser
fin si
fin si
regresa T
fin de la función
Un buen ejemplo de borrado por este algoritmo está presente en la publicación de Andersson.
Rendimiento
El rendimiento de un árbol AA es equivalente al de un árbol rojo-negro. Un árbol AA realiza más rotaciones que un árbol red-black, pero la mayor sencillez de sus algoritmos tiende a hacerlos más rápidos, y estos factores se compensan resultando en un rendimiento similar. Un árbol rojo-negro es más constante en su rendimiento que un árbol AA, pero un árbol AA tiende a ser más llano lo que produce unos tiempos de búsqueda ligeramente más pequeños.[1]
Véase también
Referencias
- «A Disquisition on The Performance Behavior of Binary Search Tree Data Structures (pages 67-75)». Archivado desde el original el 27 de marzo de 2014. Consultado el 5 de junio de 2012.
Enlaces externos
- A. Andersson. Balanced search trees made simple
- A. Andersson. A note on searching in a binary search tree
- AA-Tree Applet by Kubo Kovac
- AA Visual 2007 1.5 - OpenSource Delphi program for educating AA tree structures
- Thorough tutorial with lots of code
- Practical implementation
- Object Oriented implementation with tests
- Comparison of AA trees, red-black trees, treaps, skip lists, and radix trees Archivado el 28 de septiembre de 2007 en Wayback Machine.
- An example C implementation